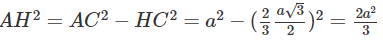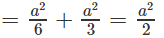30 Bài tập về mặt cầu ngoại tiếp tứ diện (2024) có đáp án

30 Bài tập về mặt cầu ngoại tiếp tứ diện

I. Phương pháp giải

Bước 1: Xác định tâm của đáy từ đó dựng đường thẳng d vuông góc với mặt đáy.

Bước 2: Dựng mặt phẳng trung trực (P) của cạnh bên bất kì.

Bước 3: Tâm của mặt cầu là giao điểm của d và (P).

Hình chóp có cạnh bên vuông góc với mặt đáy

Hình chóp có mặt bên vuông góc với đáy

II. Bài tập vận dụng

Câu 1: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng 3a. Tính bán kính mặt cầu ngoại tiếp khối chóp đã cho.

Câu 2: Cho tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc với nhau và OA=a, OB=2a, OC=2a. Tính bán kính mặt cầu ngoại tiếp tứ diện OABC.

Câu 4: Cho hình chóp SABCD có đáy ABCD là hình vuông. SA vuông góc với mặt phẳng (ABCD) và SC=2a. Tính bán kính mặt cầu ngoại tiếp hình chóp trên.

Lời giải:

Lời giải:

Câu 7: Bán kính của mặt cầu ngoại tiếp tứ diện đều cạnh a là

Câu 8:

Tính bán kính R mặt cầu ngoại tiếp tứ diện đều ABCD cạnh a$\sqrt{2}$

Lời giải:

Câu 9:

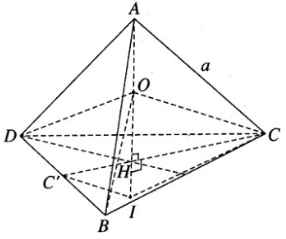
Hình tứ diện đều ABCD có cạnh bằng a và có đường cao AH. Gọi O là trung điểm của AH. Xác định tâm và bán kính của mặt cầu ngoại tiếp tứ diện OBCD.

Lời giải:

Gọi H trọng tâm của tam giác đều BCD.

Ta có AH $\perp$ (BCD). Do đó

Vậy

Mặt khác ${\mathrm{OC}}^2={\mathrm{OH}}^2+{\mathrm{HC}}^2$

hay OC = OB = OD = (a$\sqrt{2}$)/2

Vì BD = BC = CD = a nên các tam giác DOB, BOC, COD là những tam giác vuông cân tại O. Do đó hình chóp ODBC là hình chóp có đáy là tam giác đều nên tâm của mặt cầu ngoại tiếp phải nằm trên OH, ngoài ra tâm của mặt cầu ngoại tiếp này phải nằm trên trục của tam giác vuông DOB. Từ trung điểm C’ của cạnh BD ta vẽ đường thẳng song song với OC cắt đường thẳng OH tại I. Ta có I là tâm mặt cầu ngoại tiếp tứ diện OBCD. Mặt cầu này có bán kính là IC và ${\mathrm{IC}}^2={\mathrm{IH}}^2+{\mathrm{HC}}^2$

Chú ý rằng IH = OH/2 (vì HC′ = HC/2)

Do đó:

Câu 10:

Mặt cầu ngoại tiếp tứ diện vuông O.ABC có OA=OB=OC=a có bán kính bằng

Lời giải:

Câu 11:

Cho tứ diện ABCD có DA vuông góc với (ABC) và AD = a, AC = 2a; cạnh BC vuông góc với cạnh AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD.

Lời giải:

Đáp án D

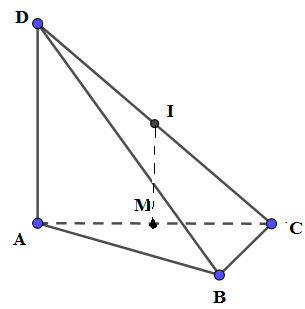
Phương pháp:

+) Xác định tâm mặt cầu ngoại tiếp khối tứ diện là điểm cách đều tất cả các đỉnh của tứ diện.

+) Áp dụng định lí Pytago tính bán kính mặt cầu ngoại tiếp tứ diện.

Cách giải:

Tam giác ABC vuông tại B, M là trung điểm của AC ⇒ M là tâm đường tròn ngoại tiếp tam giác ABC

Gọi I là trung điểm của CD ⇒ IC = ID(1)

Ta có: IM là đường trung bình của tam giác ACD ⇒ IM // AD

Mà AD ⊥ (ABC) ⇒ IM ⊥ (ABC)

Do đó, IM là trục đường tròn ngoại tiếp tam giác ABC

⇒ IA = IB = IC(2)

Từ (1), (2) ⇒ IA = IB = IC = ID ⇒ I là tâm mặt cầu ngoại tiếp tứ diện ABCD, bán kính mặt cầu:

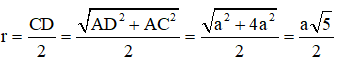
Câu 12:

Tính bán kính mặt cầu ngoại tiếp tứ giác ABCD biết rằng AB=CD=a, BC=AD=b, AC=BD=c

Lời giải:

Xem thêm các dạng bài tập hay, có đáp án:

60 Bài tập về diện tích xung quanh của hình chóp đều. Thể tích của hình chóp đều (có đáp án năm 2024)

30 Bài tập về mặt cầu ngoại tiếp hình chóp (2024) có đáp án

50 Bài tập Hình cầu. Diện tích mặt cầu và thể tích hình cầu (2024) có đáp án

60 Bài tập về mặt cầu (có đáp án năm 2024)

20 bài tập về Phương trình mặt cầu (2024) hay nhất