60 Bài tập về diện tích xung quanh của hình chóp đều. Thể tích của hình chóp đều (có đáp án năm 2024) - Toán 8

Bài giảng Toán 8 Bài 8: Diện tích xung quanh của hình chóp đều

Kiến thức cần nhớ

1. Công thức tính diện tích xung quanh của hình chóp đều

- Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn:

S_xq = p.d (trong đó p: nửa chu vi đáy, d: trung đoạn)

- Diện tích toàn phần của hình chóp

Diện tích toàn phần của hình chóp bằng tổng của diện tích xung quanh và diện tích đáy:

S_tp = S_xq + S (trong đó S: diện tích đáy)

- Ví dụ 1. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông, cạnh đáy là 3cm, chiều cao 5cm.

a) Tính diện tích xung quanh của hình chóp.

b) Tính diện tích toàn phần của hình chóp.

Lời giải:

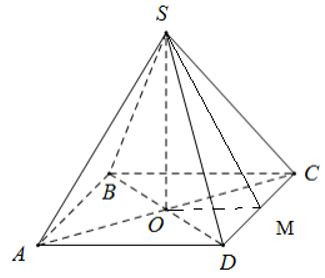
a) Ta có ABCD là hình vuông, khi đó nửa chu vi bằng: .

$\mathrm{p}=\frac{\mathrm{AB}+\mathrm{BC}+\mathrm{CD}+\mathrm{DA}}{2}=\frac{3+3+3+3}{2}=6\left(\mathrm{cm}\right)$

Kẻ SM vuông góc với CD.

Do tam giác SCD cân tại S nên SM cũng là đường trung tuyến

Suy ra M là trung điểm của CD.

Xét tam giác ACD, có:

O là trung điểm của AC

M là trung điểm của CD

Suy ra OM là đường trung bình của tam giác ACD

$\Rightarrow \mathrm{OM}=\frac{1}{2}\mathrm{AD}=\frac{1}{2}.3=\frac{3}{2}$

Xét tam giác SOM vuông tại O, có:

$$\begin{gathered} {\mathrm{SM}}^2={\mathrm{SO}}^2+{\mathrm{OM}}^2=5^2+{\left(\frac{3}{2}\right)}^2=\frac{109}{4} \\ \Rightarrow \mathrm{SM}=\frac{\sqrt{109}}{2}\mathrm{cm} \end{gathered}$$

Diện tích xung quanh của hình chóp đều là:

${\mathrm{S}}_{\mathrm{xq}}=\mathrm{p}.\mathrm{d}=\mathrm{p}.\mathrm{SM}=6.\frac{\sqrt{109}}{2}=3\sqrt{109}\left({\mathrm{cm}}^2\right)$

b) Diện tích đáy là: S = 3² = 9 cm²

+ Diện tích toàn phần của hình chóp đều là

${\mathrm{S}}_{\mathrm{tp}}={\mathrm{S}}_{\mathrm{xq}}+{\mathrm{S}}_{\mathrm{ABCD}}=3\sqrt{109}+9\left({\mathrm{cm}}^2\right)$

2. Công thức tính thể tích

Thể tích của hình chóp bằng một phần ba của diện tích đáy nhân với chiều cao:

$\mathrm{V}=\frac{1}{3}\mathrm{S}.\mathrm{h}$ (trong đó S: diện tích đáy, h: chiều cao)

Ví dụ 1. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông, cạnh đáy là 4cm, chiều cao 6cm. Tính thể tích của hình chóp.

Lời giải:

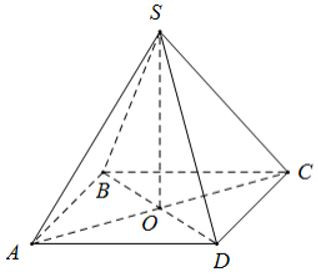
Diện tích đáy của hình chóp là: S = 4² = 16cm²

Thể tích của hình chóp đều là

$\mathrm{V}=\frac{1}{3}.{\mathrm{S}}_{\mathrm{ABCD}}.\mathrm{SO}=\frac{1}{3}.16.6=32\left({\mathrm{cm}}^3\right)$

Các dạng toán về diện tích xung quanh của hình chóp đều

(Xem chi tiết trong file đính kèm bên dưới)

Dạng toán đại lượng hình học.

Dạng toán chứng minh.

Bài tập (có hướng dẫn)

1. Bài tập vận dụng

Bài 1. Cho hình chóp tứ giác đều có các mặt bên là tam giác đều cạnh 6cm. Tính diện tích toàn phần của hình chóp?

Lời giải:

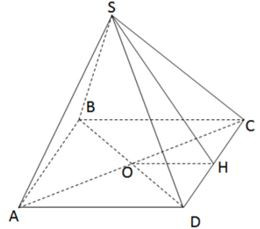
Do mặt bên của hình chóp là tam giác đều cạnh 6cm nên đáy là hình vuông cạnh 6cm.

Nửa chu vi đáy là $\mathrm{p}=\frac{6+6+6+6}{2}=12\mathrm{cm}$

Các mặt bên là tam giác đều cạnh 6cm nên độ dài trung đoạn là

$\mathrm{d}=\mathrm{SH}=\frac{6\sqrt{3}}{2}=3\sqrt{3}\mathrm{cm}$

Diện tích xung quanh là ${\mathrm{S}}_{\mathrm{xq}}=\mathrm{p}.\mathrm{d}=12.3\sqrt{3}=36\sqrt{3}{\mathrm{cm}}^2$

Diện tích đáy là: 6² = 36cm²

Diện tích toàn phần là: ${\mathrm{S}}_{\mathrm{tp}}=36\sqrt{3}+36 {\mathrm{cm}}^2$

Bài 2. Một hình chóp tứ giác đều S.ABCD có độ dài cạnh bên là 5cm và đáy là hình vuông cạnh 8cm.Tính diện tích xung quanh của hình chóp?

Lời giải:

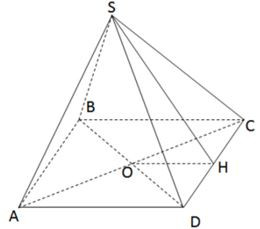
Nửa chu vi đáy là: $\mathrm{p}=\frac{8+8+8+8}{2}=16\mathrm{cm}$

Gọi H là trung điểm của CD, suy ra: CH = DH = 4cm

Áp dụng định lí Pytago vào tam giác vuông SHC có:

SH² = SC² – CH² = 5² – 4² = 9 nên SH = 3cm

Diện tích xung quanh của hình chóp là;

 S_xq= p. SH = 16. 3 = 48 cm²

Bài 3. Một hình chóp đều có độ dài cạnh bên là 13cm, đáy là tam giác đều ABC. Biết độ dài trung đoạn bằng 12 cm. Tính diện tích xung quanh của hình chóp.

Lời giải:

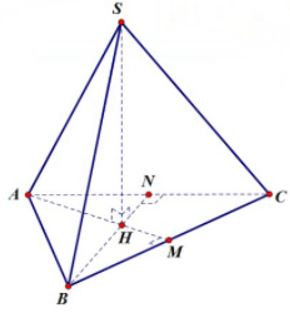
Gọi M là trung điểm của BC.

Theo giả thiết ta có: SM = 12 cm; SC = 13cm

Áp dụng định lí Pytago vào tam giác vuông SMC có:

MC² = SC² – SM² = 13² – 12² = 25

Suy ra: MC = 5cm.

Vì M là trung điểm BC nên BC = 2MC = 10cm.

Vì đáy là tam giác đều nên AB = BC= CA = 10cm

Nửa chu vi đáy là $\mathrm{p}=\frac{\mathrm{AB}+\mathrm{BC}+\mathrm{CA}}{2}=15\mathrm{cm}$

Diện tích xung quanh là: S_xq = p.d = 15. 12 = 180cm².

Bài 4. Cho hình chóp S.MNPQ có đáy là hình chữ nhật và MN = 3cm; NP = 4cm .

Biết thể tích của hình chóp S.MNPQ bằng 48cm³. Tính độ dài đường cao của hình chóp?

Lời giải:

Diện tích đáy của hình chóp là:

S = MN. NP = 3.4 = 12cm²

Áp dụng công thức thể tích của hình chóp ta có:

$\mathrm{V}=\frac{1}{3}.\mathrm{h}.\mathrm{S}\Rightarrow \mathrm{h}=\frac{3\mathrm{V}}{\mathrm{S}}=\frac{3.48}{12}=12\left(\mathrm{cm}\right)$

Vậy chiều cao của hình chóp là 12cm.

Bài 5. Một hình chóp tứ giác đều S.ABCD có cạnh bên SA = 5cm và độ dài cạnh đáy là cm. Tính thể tích của hình chóp tứ giác đều.

Lời giải:

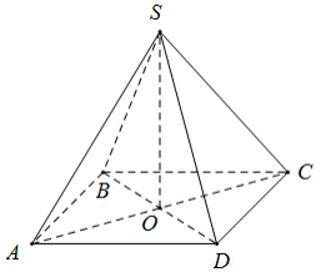
Gọi O là giao điểm của AC và BD.

Áp dụng định lí Pytago vào tam giác vuông ABC có;

AC² = AB² + BC² = ${\left(3\sqrt{2}\right)}^2+{\left(3\sqrt{2}\right)}^2=36$

Suy ra: AC = 6 cm và $\mathrm{AO}=\frac{1}{2}\mathrm{AC}=3\mathrm{cm}$

Áp dụng định lí Pytago vào tam giác vuông SAO có:

 SO² = SA² -  AO² =  5² -  3² = 16 nên SO = 4cm

Diện tích đáy là: ${\left(3\sqrt{2}\right)}^2=18{\mathrm{cm}}^2$

Thể tích của hình chóp là: $\mathrm{V}=\frac{1}{3}.18.4=24{\mathrm{cm}}^3$

Vậy thể tích của hình chóp là 24 cm³_.

Bài 6. Cho hình chóp tam giác đều S.ABC có thể tích là $12\sqrt{3}$ cm³; chiều cao của hình chóp là 4cm. Tính độ dài cạnh đáy?

Lời giải:

Thể tích của hình chóp đều là:

$\mathrm{V}=\frac{1}{3}{\mathrm{S}}_{\mathrm{d}}.\mathrm{h}\Rightarrow {\mathrm{S}}_{\mathrm{d}}=\frac{3\mathrm{V}}{\mathrm{h}}=\frac{3.12\sqrt{3}}{4}=\frac{36\sqrt{3}}{4}{\mathrm{cm}}^2$

Gọi độ dài cạnh đáy là a.

Do đáy là tam giác đều nên diện tích đáy là  ${\mathrm{S}}_{\mathrm{d}}=\frac{{\mathrm{a}}^2\sqrt{3}}{4}{\mathrm{cm}}^2$

Suy ra: $\frac{{\mathrm{a}}^2\sqrt{3}}{4}=\frac{36\sqrt{3}}{4}\iff {\mathrm{a}}^2=36\iff \mathrm{a}=6\mathrm{cm}$.

Vậy độ dài cạnh đáy là 6cm

2. Bài tập tự luyện

(Xem trong file đính kèm bên dưới)

Xem thêm các dạng bài tập liên quan khác:

50 bài tập về hình bình hành (có đáp án 2024)

50 bài tập về hình thang, hình thang vuông, hình thang cân (có đáp án 2024)

50 bài tập về diện tích hình chữ nhật (có đáp án 2024)

50 bài tập về đa giác, Đa giác lồi, Đa giác đều (có đáp án 2024)

60 Bài tập về hình chóp đều và hình chóp cụt đều (có đáp án năm 2024)