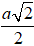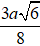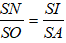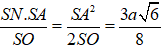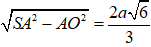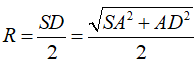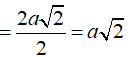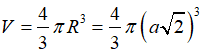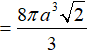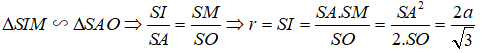30 Bài tập về mặt cầu ngoại tiếp hình chóp (2024) có đáp án

30 Bài tập về mặt cầu ngoại tiếp hình chóp

I. Phương pháp giải

+ Xác định trục d của đường tròn ngoại tiếp đa giác đáy (d là đường thẳng vuông góc với đáy tại tâm đường tròn ngoại tiếp đa giác đáy).

+ Xác định mặt phẳng trung trực (P) của một cạnh bên (hoặc trục Δ của của đường tròn ngoại tiếp một đa giác của mặt bên).

+ Giao điểm I của (P) và d (hoặc của Δ và d ) là tâm mặt cầu ngoại tiếp.

+ Kết luận: I là tâm mặt cầu ngoại tiếp chóp.

Nhận xét: Hình chóp có đáy hoặc các mặt bên là các đa giác không nội tiếp được đường tròn thì hình chóp đó không nội tiếp được mặt cầu.

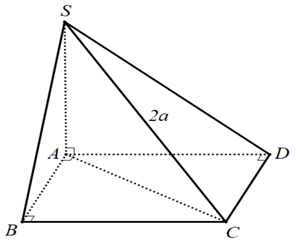
Ví dụ 1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt phẳng (ABCD) và SC= 2a. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABC.

A. a    B. 2a    C. a√2 .    D. 

Hướng dẫn giải:

▪ Ta có: 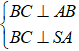 ⇒ BC ⊥ (SAB) ⇒ BC ⊥ SB .

▪ Chứng minh tương tự ta được CD ⊥ SD .

▪ SA ⊥ (ABCD) ⇒ SA ⊥ AC .

Suy ra: Ba điểm A, B, D cùng nhìn SC dưới một góc vuông.

Vậy bán kính mặt cầu là R = SC/2 = a .

Chọn A.

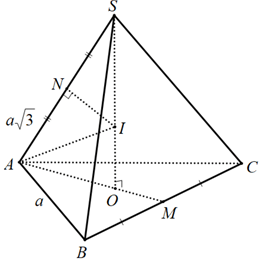
Ví dụ 2. Tính bán kính của mặt cầu ngoại tiếp hình chóp tam giác đều S. ABC, biết các cạnh đáy có độ dài bằng a, cạnh bên SA = a√3 .

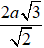
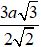
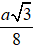
A.     B.     C.     D. 

Hướng dẫn giải:

Gọi O là tâm của tam giác đều ABC.

+ Ta có SO ⊥ (ABC) nên SO là trục của đường tròn ngoại tiếp tam giác ABC.

+ Gọi N là trung điểm của SA, trong mp(SAO) kẻ trung trực của SA cắt SO tại I thì IS= IA= IB= IC nên I chính là tâm mặt cầu ngoại tiếp hình chóp S. ABC. Bán kính mặt cầu là R= SI.

+ Vì hai tam giác SNI và SOA đồng dạng nên ta có 

Suy ra R = SI = 

Mà AO =  ,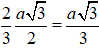
SO = 

Nên R = SI = 

Chọn D.

II. Bài tập vận dụng

Bài 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tại A, SA vuông góc với mặt phẳng  (ABCD) và SC = 2a. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.

Lời giải:

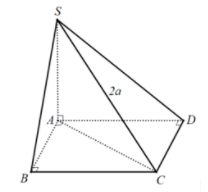
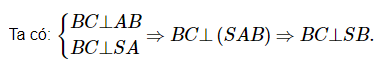
Chứng minh tương tự ta được: CD ⊥ SD

SA ⊥ (ABCD) ⇒ SA ⊥ AC

Ba điểm A, B, D cùng nhìn SC dưới một góc vuông.

Vậy bán kính mặt cầu là R = SC/2 = 2a/2 = a

Bài 2: 

Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a.

Lời giải:

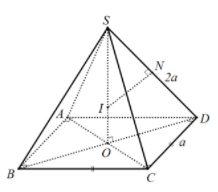
Gọi O là tâm đáy thì SO là trục của hình vuông ABCD. Gọi N là trung điểm của SD, trong (SDO) kẻ trung trực của đoạn SD cắt SO tại I thì IS = IA = IB = IC = ID nên I là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD . Bán kính mặt cầu là R = SI.

Ta có: ΔSNI ∼ ΔSOA ⇒ SN/SO = SI/SD ⇒ R = SI = SD. SN / SO = SD²/SO

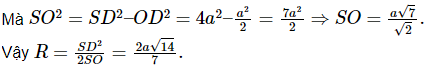
Bài 3: 

Cho hình chóp S.ABC có cạnh SA vuông góc với đáy, ABC là tam giác cân tại A và AB = a, góc BAC = 120⁰, SA = 2a. Tính bán kính của mặt cầu ngoại tiếp hình chóp S.ABC

Lời giải:

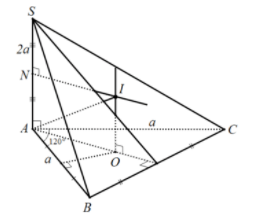
Gọi O là tâm đường tròn ngoại tiếp của tam giác ABC.

Dựng trục d của đường tròn ngoại tiếp tam giác ABC; trong mặt phẳng (SA,d) vẽ trung trực cạnh SA và cắt d tại I.

Suy ra I là tâm mặt cầu ngoại tiếp hình chóp S.ABC và bán kính R = IA = IB = IC = IS

Bài 4: 

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.

Lời giải:

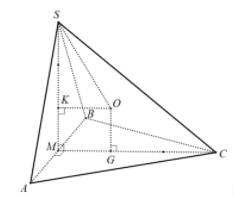
Bài 5: 

Tính bán kính của mặt cầu ngoại tiếp hình chóp tam giác đều S,ABC, biết các cạnh đáy có độ dài bằng a , cạnh bên SA = a$\sqrt{3}$.

Lời giải:

Bài 6: 

Cho hình chóp S.ABC có SA$\perp$(ABC), ABC là tam giác vuông tại A, AB=3a; AC=4a; SA=5a. Tìm bán kính mặt cầu mặt cầu ngoại tiếp hình chóp S.ABC?

Lời giải:

Bài 7: 

Cho hình chóp S.ABC có SA$\perp$(ABC), tam giác ABC vuông tại B,SA=BC=3.

Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho. 

Lời giải:

Bài 8: 

Cho hình chóp S.ABCD đáy là hình thang cân có AB=BC=CD. Cạnh bên SA vuông góc với đáy, SA=2a. Thể tích khối cầu ngoại tiếp hình chóp S.BCD là: