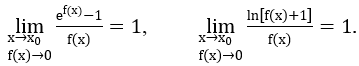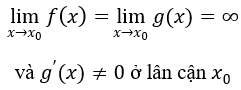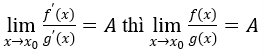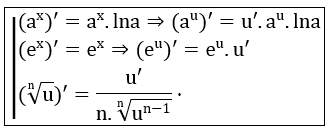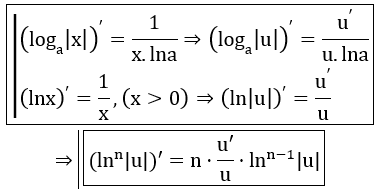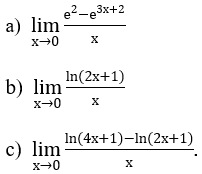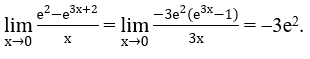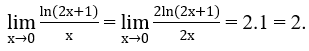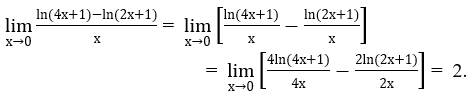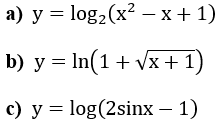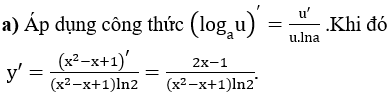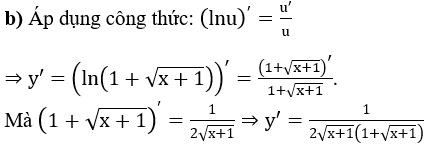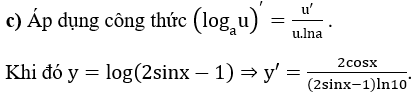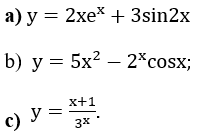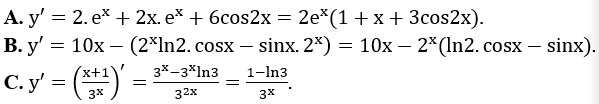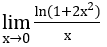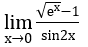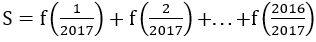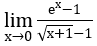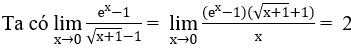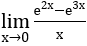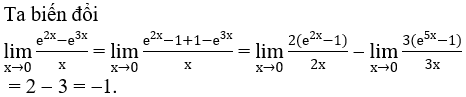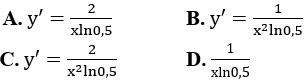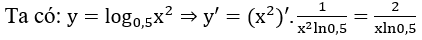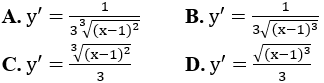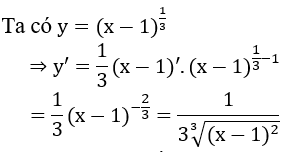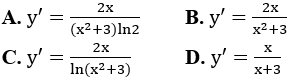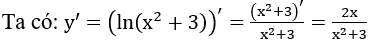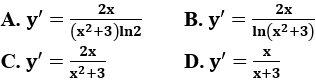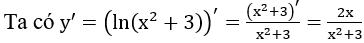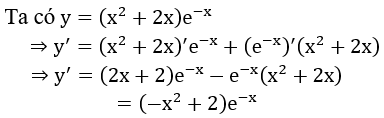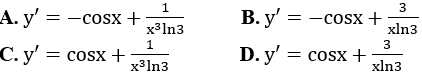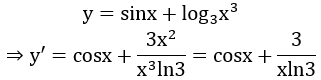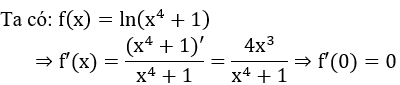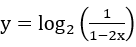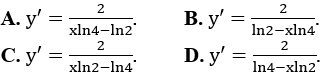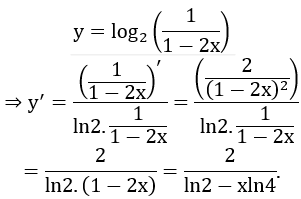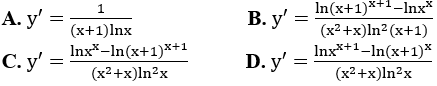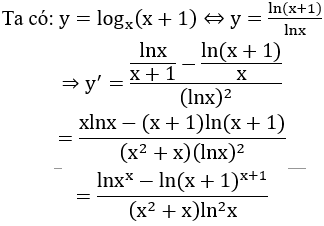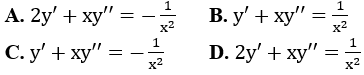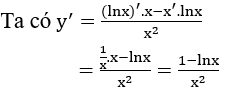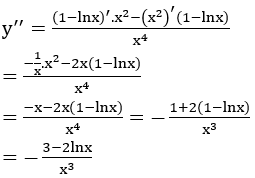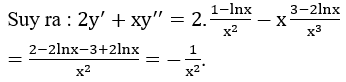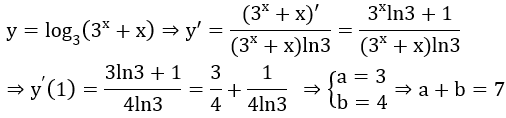30 bài tập về Giới hạn, đạo hàm của hàm số mũ, lũy thừa, lôgarit (2024) có đáp án, cực hay

Giới hạn, đạo hàm của hàm số mũ, lũy thừa, lôgarit

PHƯƠNG PHÁP GIẢI

Bài toán 1: Giới hạn của hàm số mũ, hàm số Logarit

    Phương pháp

        Chúng ta có các dạng giới hạn đặc biệt sau:

    Mở rộng: Ta có

    Quy tắc Lopitan: Nếu f(x), g(x) khả vi ở lân cận x₀ trừ tại điểm x₀ thì:

    Đồng thời

    Quy tắc vẫn đúng với x → ∞

Bài toán 2: Đạo hàm của các hàm số lũy thừa, hàm số mũ, hàm số logarit

    Phương pháp:

        - Hàm số lũy thừa:

        Hàm số y = x^α, (α ∈ R) có đạo hàm với mọi x > 0 và (x^α)' = α.x^α-1.

        - Hàm số mũ:

        - Hàm số Logarit:

VÍ DỤ MINH HỌA

Ví dụ 1: Tìm các giới hạn sau:

Lời giải:

a) Ta biến đổi

b) Ta biến đổi

c) Ta biến đổi

Ví dụ 2: Tính đạo hàm của các hàm số sau:

Lời giải:

Ví dụ 3: Tính đạo hàm của các hàm số sau:

Lời giải:

BÀI TẬP VẬN DỤNG (CÓ ĐÁP ÁN)

Bài 1: Tìm giới hạn sau

Lời giải:

Bài 2: Tìm giới hạn sau

Lời giải:

Bài 3: Tính đạo hàm của hàm số 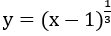 tại điểm x = 2

Lời giải:

Áp dụng công thức (u^α)' = α.u^α-1.u'.

Bài 4: Tính đạo hàm của hàm số y = log(ln2x).

Lời giải:

Bài 5: Tính đạo hàm của hàm số

Lời giải:

Bài 6: Tính đạo hàm của hàm số

Lời giải:

Bài 7: Tính đạo đạo hàm của hàm số y=log₃(x+1)-2ln(x-1)+2x tại điểm x = 2

Lời giải:

Bài 8: Cho hàm số 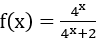. Tính tổng T

Lời giải:

Nên

Bài 9: Cho 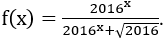. Tính giá trị biểu thức S

Lời giải:

Nên

Bài 10: Cho hàm số y = ln(2x² + e²). Nếu 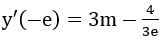 thì giá trị m bằng bao nhiêu?

Lời giải:

Ta có

BÀI TẬP TỰ LUYỆN (CÓ HƯỚNG DẪN)

Bài 1: Tìm giới hạn của

A.0        B. 1        C. 2        D. 3

Lời giải:

Đáp án :

Giải thích :

Bài 2: Tìm giới hạn của

A. 0        B. -1        C. -2        D. 1

Lời giải:

Đáp án :

Giải thích :

Bài 3: Hàm số y = log_0,5x² (x ≠ 0) có công thức đạo hàm là:

Lời giải:

Đáp án :

Giải thích :

Bài 4: Đạo hàm của hàm số y = 4^2x là:

A. y' = 2.4^2xln4        B. y' = 4^2x.ln2

C. y' = 4^2xln4        D. y' = 2.4^2xln2

Lời giải:

Đáp án :

Giải thích :

y = 4^2x ⇒ y' = (2x)'.4^2xln4 = 2.4^2xln4

Bài 5: Hàm số 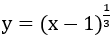 có đạo hàm là:

Lời giải:

Đáp án :

Giải thích :

Bài 6: Cho hàm số y = log₂(2^x+1). Khi đó y'(1) bằng :

Lời giải:

Đáp án :

Giải thích :

Bài 7: Tính đạo hàm của hàm số y=ln(x²+3)

Lời giải:

Đáp án :

Giải thích :

Bài 8: Tính đạo hàm của hàm số y=(x²+2x)e^-x

A. y'=(x²+2)e^-x        B. y'=(-x²+2)e^-x

C. y'=xe^-x        D. y'=(2x-2)e^x

Lời giải:

Đáp án :

Giải thích :

Bài 9: Đạo hàm của hàm số y = sinx+log₃x³ (x > 0) là:

Lời giải:

Đáp án :

Giải thích :

Ta có

Bài 10: Cho hàm số f(x)=ln(x⁴+1). Đạo hàm f' (0)bằng:

A. 2        B. 1        C. 0        D. 3

Lời giải:

Đáp án :

Giải thích :

Bài 11: Cho hàm số f(x) = xe^x. Gọi f'' (x)là đạo hàm cấp hai của f(x). Ta có f'' (1) bằng:

A. -3e²        B. 3e        C. e³        D. -5e²

Lời giải:

Đáp án :

Giải thích :

Ta có f(x) = x.e^x ⇒ f'(x)=e^x + x.e^x ⇒ f''(x) = e^x + e^x + x.e^x ⇒ f''(1)=3e

Bài 12: Tính đạo hàm của hàm số

Lời giải:

Đáp án :

Giải thích :

Bài 13: Tính đạo hàm của hàm số y = log_x(x+1)

Lời giải:

Đáp án :

Giải thích :

Bài 14: Cho hàm số y=(lnx)/x, mệnh đề nào dưới đây đúng?

Lời giải:

Đáp án :

Giải thích :

Bài 15: Cho hàm số y = log₃(3^x+x), biết 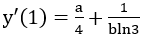 với a,b∈Z. Tính giá trị của a+b.

A. 2        B. 7        C. 4        D. 1

Lời giải:

Đáp án :

Giải thích :

Xem thêm các dạng bài tập Toán chi tiết và hay khác:

60 Bài tập về Hàm số lũy thừa (có đáp án năm 2023)

60 Bài tập về Lôgarit (có đáp án năm 2023)

60 Bài tập về Phương trình mũ và phương trình logarit (có đáp án năm 2023)

60 Bài tập về Bất phương trình mũ và bất phương trình logarit (có đáp án năm 2023)

60 Bài tập về Nguyên hàm ( có đáp án năm 2023 )