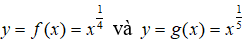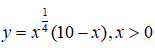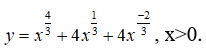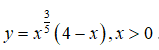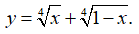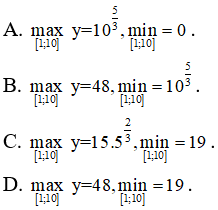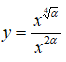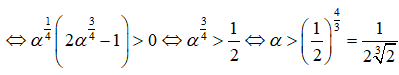Bài tập về Hàm số lũy thừa
Kiến thức cần nhớ
1. Khái niệm
– Hàm số y = xα, với α∈ ℝ, được gọi là hàm số lũy thừa.
Ví dụ 1. Các hàm số y= x√3+1 ; y= 1x2; y= x5; y= xπ−3 là những hàm số lũy thừa.
– Chú ý:
Tập xác định của hàm số lũy thừa y = xα tùy thuộc vào giá trị của α. Cụ thể:
+ Với α nguyên dương, tập xác định là R.
+ Với α nguyên âm hoặc bằng 0; tập xác định là R\{0}.
+ Với α không nguyên, tập xác định là (0; + ∞).
2. Đạo hàm của hàm số lũy thừa
– Hàm số lũy thừa y = xα ( α∈ℝ) có đạo hàm với mọi x > 0 và (xα)'.
– Ví dụ 2.
a)
b)
– Chú ý: Công thức tính đạo hàm của hàm hợp đối với hàm số lũy thừa có dạng:
– Ví dụ 3. Tính đạo hàm của hàm số
Lời giải:
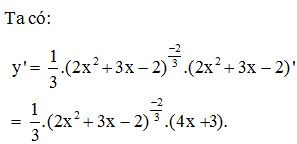
3. Khảo sát hàm số lũy thừa y = xα
Tập xác định của hàm số lũy thừa luôn chứa khoảng với . Trong trường hợp tổng quát, ta khảo sát hàm số trên khoảng này (gọi là tập khảo sát).

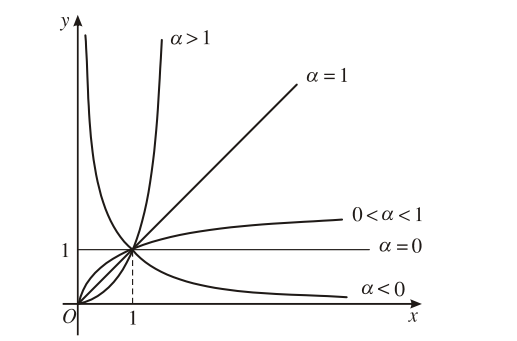
Đồ thị của hàm số lũy thừa y = xα luôn đi qua điểm (1; 1).
– Chú ý: Khi khảo sát hàm số lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó.
Ví dụ 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số .
Lời giải:
1. Tập xác định:
2. Sự biến thiên.
Chiều biến thiên
Ta có: y’ < 0 trên khoảng nên hàm số đã cho nghịch biến.
Tiệm cận:
Đồ thị có tiệm cận ngang là trục hoành và có tiệm cận đứng là trục tung.
Bảng biến thiên
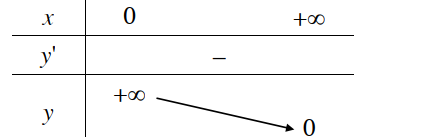
3. Đồ thị
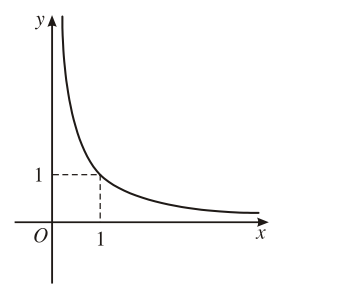
Bảng tóm tắt các tính chất của hàm số lũy thừa trên khoảng .
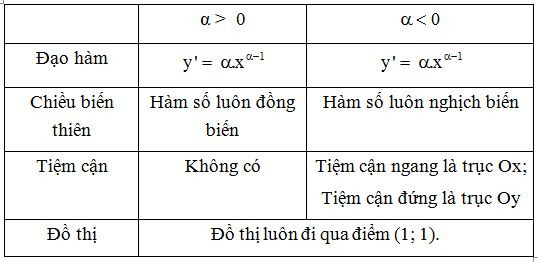
Các dạng bài tập về hàm số lũy thừa
Dạng 1. Tìm tập xác định của hàm số lũy thừa.
Dạng 2. Đồ thị hàm số lũy thừa.
Bài tập
1. Bài tập vận dụng (có đáp án chi tiết)
Bài 1: Đồ thị hàm số y = cắt đường thẳng y=2x tại một điểm nằm bên phải trục tung. Tìm tọa độ điểm này.
Lời giải:
Phương trình hoành độ giao điểm
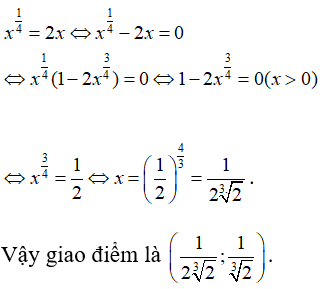
Bài 2: Tìm đạo hàm của hàm số
Lời giải:
Viết lại hàm số dưới dạng lũy thừa
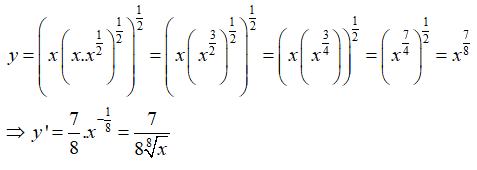
Bài 3: Đường thẳng x = α ( α là số thực dương) cắt đồ thị các hàm số
lần lượt tại hai điểm A và B. Biết rằng tung độ điểm A bé hơn tung độ điểm B. Khẳng định nào sau đây là đúng?
Lời giải:
Từ giả thiết suy ra f(α) < g(α)
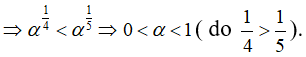
Nhận xét. Ở đây ta sử dụng tính chất:
Nếu a > 1 thì aα > aβ <=> α > β ;
Nếu 0 < a < 1 thì aα > aβ <=> α < β .
Học sinh có thể không áp dụng tính chất trên mà giải tiếp:
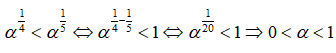
Bài 4: Cho hàm số
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên (0;2).
B. Hàm số nghịch biến trên khoảng (5; +∞) .
C. Hàm số đồng biến trên (2; +∞) .
D. Hàm số không có điểm cực trị nào.
Ta có
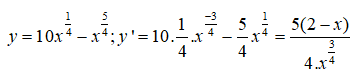
Ta thấy y'(x) < 0 <=> x > 2 nên hàm số nghịch biến trên (2; +∞) , và do đó, hàm số nghịch biến trên (5; +∞) .
Bài 5: Tìm các điểm cực trị của hàm số
Lời giải:
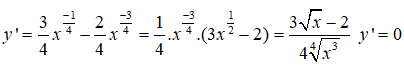
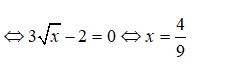
y’ đổi dấu khi qua điểm x = nên hàm số có một điểm cực trị là x = .
Bài 6: Tìm các điểm cực trị của hàm số
Lời giải:
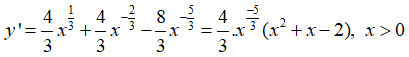
y'= 0 <=> x2 + x - 2 = 0 <=> x = -2 (loại) hoặc x = 1
y' đổi dấu khi đi qua điểm x = 1 nên hàm số có một điểm cực trị là x = 1
Bài 7: Tìm các điểm cực trị của hàm số
Lời giải:
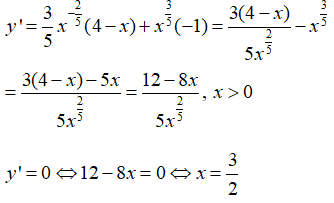
y’ đổi dấu khi đi qua điểm x = nên hàm số có một điểm cực trị là x =
Bài 8: Tìm các giá trị lớn nhất và nhỏ nhất của hàm số
Lời giải:
Tập xác định D = [0; 1]
Ta có:
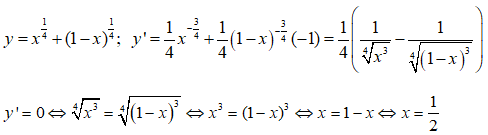
y(0) = y(1) = 1; y() = . Từ đó max y = y() = , min y = y(0) = 1
Bài 9: Tìm các giá trị lớn nhất và nhỏ nhất của hàm số y = (20 - x) trên đoạn [1; 10]
Lời giải:
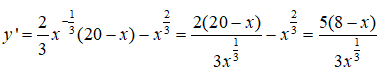
y' = 0 <=> x = 8
Ta có: y(1) = 19, y(8) = 48, y(10) = ≈ 46,6 > 19
Từ đó:
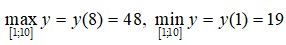
Bài 10: Với là một số thực dương và hàm số
nghịch biến trên khoảng (0; +∞). Khẳng định nào sau đây là đúng?
Lời giải:
Hàm số
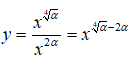
nghịch biến trên (0; +∞) nên - 2α < 0
2. Bài tập tự luyện có hướng dẫn
(Xem trong file đính kèm)
Xem thêm các dạng bài tập liên quan khác:
60 Bài tập về Hàm số lũy thừa (có đáp án năm 2023)
50 Bài tập về lũy thừa với số mũ tự nhiên (có đáp án năm 2023)
60 Bài tập lũy thừa với số mũ tự nhiên của một số hữu tỉ (có đáp án năm 2023)
40 bài tập lũy thừa và cách giải lớp 7 hay nhất (2024)
Cách giải bài toán rút gọn biểu thức chứa lũy thừa (2024) dễ nhất