30 Bài tập tìm m để bất phương trình vô nghiệm (2024) có đáp án

Chọn D

+ Xét bpt : 3x-4> x+ 9 hay x> 5/ 2

Suy ra tập nghiệm của bpt đầu là : S₁= ( 5/2; + ∞)

+ Xét bpt: 1-2x ≤ m-3x+ 1

Hay x ≤ m

Suy ra tập nghiệm của bpt thứ 2 là S₂= ( -∞; m]

Để hệ bpt vô nghiệm khi và chỉ khi :

Bài 2:

Tìm m để hệ bất phương trình sau vô nghiệm

$\left\{\begin{array}{c}3\mathrm{x}+5\ge \mathrm{x}-1\\ {\left(\mathrm{x}+2\right)}^2\le {\left(\mathrm{x}-1\right)}^2+9\\ \mathrm{mx}+1>\left(\mathrm{m}-2\right)\mathrm{x}+\mathrm{m}\end{array}\right.$

Lời giải:

Chọn B

+ Bpt: 3x+ 5 ≥ x- 1 hay 2x ≥ - 6

Suy ra: x ≥ - 3

Tập nghiệm S₁= [-3; + ∞)

+ Bpt : (x+ 2) ² ≤ ( x-1) ²+ 9

Hay 4x+4 ≤ -2x+ 1+ 9

Suy  ra: 6x ≤ 6

Do đó; x ≤ 1 và S₂= ( -∞; 1]

Suy ra : 

+ Xét bpt : mx+ 1> ( m-2) x+ m

Tương đương : 2x> m-1

Hay  

từ đó tập nghiệm 

+ Để hệ bpt vô nghiệm khi và chỉ khi 

Suy ra : 

Bài 3:

Tìm m để bất phương trình sau vô nghiệm

    $5x^2 - x + m \le 0$

Lời giải:

Bất phương trình đã cho vô nghiệm khi và chỉ khi $5x^2 - x + m \le 0$ nghiệm đúng với mọi x.

    ⇔ 1 - 20m < 0 ⇔ m > 1/20

    Đáp số: m > 1/20

Bài 4:

Lời giải:

Đáp án đúng là: B

Ta có f(x) > 0 vô nghiệm $\iff$ f(x) ≤ 0, ∀x $\in$ ℝ.

Xét m = 3, f(x) = 5x – 4 > 0 $\in$ x > $\frac{4}{5}$ nên loại m = 3.

Xét m ≠ 3, f(x) ≤ 0, ∀x $\in$ ℝ $\iff$ $\left\{\begin{array}{c}a=m-3<0\\ \Delta =m^2+20m-44\le 0\end{array}\right.$ $\iff$ −22 ≤ m ≤ 2.

Bài 5:

Với giá trị nào của m thì bất phương trình m²x+ 4m - 3 < x + m² vô nghiệm?

Lời giải:

Chọn B

Bài 6:

Tìm các giá trị của m để bất phương trình sau vô nghiệm:

f(x) = (m + 1)$x^2$ - 2(3 - 2m)x + m + 1 ≥ 0

Lời giải:

f(x) = (m + 1)$x^2$ - 2(3 - 2m)x + m + 1 ≥ 0 (1)

Với m = -1:

(1) ⇔ -10x ≥ 0 ⇔ x ≤ 0

Vậy với m = -1 bất phương trình (1) có nghiệm x ≤ 0

Suy ra, m = -1 (loại)

Với m ≠ -1:

f(x) = (m +1 )$x^2$ - 2(3 - 2m)x + m + 1

Δ' = [-(3 - 2m)${]}^2$ - (m + 1)(m + 1) = (2m - 3${)}^2$ - (m + 1${)}^2$

= (2m - 3 + m + 1)(2m - 3 - m - 1) = (3m - 2)(m - 4)

Để bất phương trình (1) vô nghiệm thì:

Vậy không có giá trị nào của m để bất phương trình (1) vô nghiệm

Bài 7:

Bất phương trình $m{x}^2-2(m+1)x+m+7 <\hspace{0.17em}0$ vô nghiệm khi:

Lời giải:

Chọn A.

ĐK: 

TH1: m = 0: 

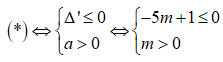
TH2:

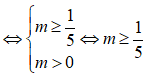
Vậy BPT đã cho vô nghiệm khi $m \ge \frac{1}{5}$

Bài 8:

Tìm m để các bất phương trình sau vô nghiệm

a) $5x^2–x+m\le 0;$

b) $m{x}^2–10x–5\ge 0.$

Lời giải:

a) Bất phương trình đã cho vô nghiệm khi và chỉ khi $5x^2–x+m>0$ nghiệm đúng với mọi x.

$\iff 1–20m<0\iff m>\frac{1}{20}$

Đáp số: $m>\frac{1}{20}$

b) Cần tìm m để $m{x}^2–10x–5>0,\mathrm{\forall }x$ (1)

Nếu m = 0 thì bất phương trình (1) trở thành $$–10x–5<0$$không nghiệm đúng với mọi x.

Nếu $m\ne 0$ thì bất phương trình (1) nghiệm đúng khi và chỉ khi 

$\{\begin{array}{c}m<0\hfill \\ \mathrm{\Delta }‘=25+5m<0\hfill \end{array}\iff m<–5$

Đáp số: m < -5.

Bài 9:

Tìm các giá trị của m để mỗi hệ bất phương trình sau vô nghiệm

a) 

$\{\begin{array}{c}2x+7<8x–1\hfill \\ –2x+m+5\ge 0\hfill \end{array}$

b) 

$\{\begin{array}{c}(x–3{)}^2\ge x^2+7x+1\hfill \\ 2m–5x\le 8\hfill \end{array}$

Lời giải:

a) Ta có:

$\{\begin{array}{c}2x+7<8x–1\hfill \\ –2x+m+5\ge 0\hfill \end{array}\iff \{\begin{array}{c}x>\frac{4}{3}\hfill \\ x\le \frac{m+5}{2}\hfill \end{array}$ 

Hệ bất phương trình vô nghiệm khi và chỉ khi:

$\begin{array}{rl}& \frac{m+5}{2}\le \frac{4}{3}\\ & \iff 3m+15\le 8\iff 3m\le –7\iff m\le –\frac{7}{3}\end{array}$

b) Ta có:

$\begin{array}{rl}& \{\begin{array}{c}(x–3{)}^2\ge x^2+7x+1\hfill \\ 2m–5x\le 8\hfill \end{array}\\ & \iff \{\begin{array}{c}{x}^2–6x+9\ge x^2+7x+1\hfill \\ 5x\ge 2m–8\hfill \end{array}\\ & \iff \{\begin{array}{c}x\le \frac{8}{13}\hfill \\ x\ge \frac{2m–8}{5}\hfill \end{array}\end{array}$

Hệ bất phương trình vô nghiệm:

$\begin{array}{rl}& \iff \frac{2m–8}{5}>\frac{8}{13}\iff 26m–104>40\\ & \iff 26m>144\\ & \iff m>\frac{72}{13}\end{array}$

Bài 10:

Tìm tất cả các giá trị của tham số m để các bất phương trình sau vô nghiệm:

a) $3x^2+mx+m+2<0;$

b) $\left(3–m\right)x^2–2\left(2m–5\right)x–2m+5>0$.

Lời giải:

a) Bất phương trình đã cho có hệ số $a=3>0$, để bất phương trình vô nghiệm, điều kiện cần và đủ là :

$\begin{array}{l}\mathrm{\Delta }=m^2–12\left(m+2\right)\le 0\\ \iff m^2–12m–24\le 0\\ \iff 6–2\sqrt{15}\le m\le 6+2\sqrt{15.}\end{array}$

b) Với $m=3$, khi đó bất phương trình trở thành $–2x–1>0$ và bất phương trình có nghiệm là $x<–{\displaystyle \frac{1}{2}}.$ Suy ra $m=3$ không thỏa mãn.

Với $m\ne 3$. Để bất phương trình vô nghiệm điều kiện cần và đủ là:

$\begin{array}{l}\{\begin{array}{l}3–m<0\\ \mathrm{\Delta }‘={\left(2m–5\right)}^2–\left(3–m\right)\left(5–2m\right)<0\end{array}\\ \iff \{\begin{array}{l}m>3\\ 2m^2–9m+10<0\end{array}\\ \iff \{\begin{array}{l}m>3\\ 2<m<{\displaystyle \frac{5}{2}}.\end{array}\end{array}$

Suy ra không tồn tại m để bất phương trình đã cho vô nghiệm.

Bài 11:

Chứng minh rằng các phương trình sau vô nghiệm dù m lấy bất kỳ giá trị nào.

a) x² – 2(m + 1)x + 2m² + m + 3 = 0

b) (m² + 1)x² + 2(m + 2)x + 6 = 0

Lời giải:

a) Ta có:

Δ’ = (m + 1)² – (2m² + m  + 3) = -m² + m – 2 < 0 ∀m

(do a = -1 < 0 và Δ_m = -7 < 0)

Vậy phương trình đã cho vô nghiệm với mọi m.

b) Ta có:

Δ’ = (m + 2)² – 6(m² + 1) = -5m² + 4m – 2 < 0 ∀m

(vì a = -5 < 0 và Δ’_m = -6 < 0)

Vậy phương trình đã cho vô nghiệm với mọi m.

Xem thêm các dạng bài tập hay, có đáp án: