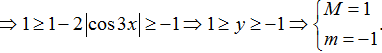30 bài tập các công thức tính min max 9 10 11 12 2024 (có đáp án)

1900.edu.vn xin giới thiệu bài tập và tóm tắt lý thuyết Toán: các công thức tính min max lớp 9, 10 ,11 .12 hay, chi tiết cùng với bài tập trắc nghiệm chọn lọc có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán . Mời các bạn đón xem:

Bài tập về công thức tính min max lớp 9 ,10 ,11, 12

I. Lý thuyết

- Lớp 9:

+ Cách 1: Biến đổi biểu thức về dạng tổng hoặc hiệu của một số không âm với hằng số

- Khi biến đổi biểu thức thành tổng của một số không âm với hằng số, ta sẽ tìm được giá trị nhỏ nhất của biểu thức ấy.

- Khi biến đổi biểu thức thành hiệu của một số với một số không âm, ta sẽ tìm được giá trị lớn nhất của biểu thức ấy.

+ Cách 2: Áp dụng bất đẳng thức Cauchy (Cô-si)

- Theo bất đẳng thức Cauchy với hai số a, b không âm ta có: $a + b \ge 2\sqrt {ab}$

Dấu “=” xảy ra khi và chỉ khi a = b

+ Cách 3: Áp dụng bất đẳng thức chứa dấu giá trị tuyệt đối:

|a| + |b| ≥ |a + b|. Dấu “=” xảy ra khi và chỉ khi a.b ≥ 0
|a - b| ≤ |a| + |b|. Dấu “=” xảy ra khi và chỉ khi a.b ≤ 0

- Lớp 10:

Bước 1: Tìm tập xác định (nếu đề bài không cho sẵn)

Bước 2: Tính và giải phương trình

Bước 3: Tính và

Bước 4: So sánh và kết luận.

- Lớp 11:

Để tìm được giá trị lớn nhất;giá trị nhỏ nhất của hàm số ta cần chú ý:

+ Với mọi x ta luôn có: - 1 ≤ cosx ≤ 1; -1 ≤ sinx ≤ 1

+Với mọi x ta có: 0 ≤ |cosx| ≤ 1 ;0 ≤ |sinx| ≤ 1

+ Bất đẳng thức bunhia –copski: Cho hai bộ số (a₁; a₂) và (b₁;b₂) khi đó ta có:

(a₁.b₁+ a₂.b₂ )² ≤ ( a₁²+ a₂² ).( b₁²+ b₂² )

Dấu “=” xảy ra khi: a₁/a₂ = b₁/b₂

+ Giả sử hàm số y= f(x) có giá trị lớn nhất là M và giá trị nhỏ nhất là m. Khi đó; tập giá trị của hàm số là [m; M].

+ Phương trình : a. sinx+ b. cosx= c có nghiệm khi và chỉ khi a² + b² ≥ c²

- Lớp 12:

Quy tắc tìm giá trị lớn nhất, nhỏ nhất của hàm số $y = f (x)$ liên tục trên đoạn $[a; b]$

+ Tìm các điểm $x_{i} \in (a, b) (i = 1, 2, . . . ., n)$ mà tại đó $f' (x_{i}) = 0 h o ặ c f' (x_{i})$ không xác định

+ Tính $f (a), f (b), f (x_{i}) (i = 1, 2, . . . ., n)$

+ Khi đó $\underset{[a; b]}{m a x} f (x) = m a x \{f (a), f (b), f (x_{i})\}$

$\underset{[a; b]}{m i n} f (x) = m i n \{f (a), f (b), f (x_{i})\}$

II. Ví dụ minh họa

Ví dụ 1: Tìm giá trị lớn nhất của biểu thức $A = \frac{1}{{x - \sqrt x + 1}}$

Lời giải:

Điều kiện xác định x ≥ 0

Để A đạt giá trị lớn nhất thì $x - \sqrt x + 1$ đạt giá trị nhỏ nhất

Có $x - \sqrt x + 1 = x - 2.\frac{1}{2}.\sqrt x + \frac{1}{4} - \frac{1}{4} + 1 = {\left( {\sqrt x - \frac{1}{2}} \right)^2} + \frac{3}{4}$

Lại có ${\left( {\sqrt x - \frac{1}{2}} \right)^2} \ge 0\forall x \ge 0 \Rightarrow {\left( {\sqrt x - \frac{1}{2}} \right)^2} + \frac{3}{4} \ge \frac{3}{4}\forall x \ge 0$

Dấu “=” xảy ra $\Leftrightarrow \sqrt x = \frac{1}{2} \Leftrightarrow x = \frac{1}{4}$

Min $x - \sqrt x + 1 = \frac{3}{4} \Leftrightarrow x = \frac{1}{4}$

Vậy Max $A = \frac{4}{3} \Leftrightarrow x = \frac{1}{4}$

Ví dụ 2: Cho biểu thức $A = \left( {\frac{1}{{x - \sqrt x }} + \frac{1}{{\sqrt x - 1}}} \right):\frac{{\sqrt x + 1}}{{{{\left( {\sqrt x - 1} \right)}^2}}}$

a, Rút gọn A

b, Tìm giá trị lớn nhất của biểu thức $P = A - 9\sqrt x$

Lời giải:

a, $A = \left( {\frac{1}{{x - \sqrt x }} + \frac{1}{{\sqrt x - 1}}} \right):\frac{{\sqrt x + 1}}{{{{\left( {\sqrt x - 1} \right)}^2}}}$ với x > 0, x ≠ 1

$= \left( {\frac{1}{{\sqrt x \left( {\sqrt x - 1} \right)}} + \frac{1}{{\sqrt x - 1}}} \right):\frac{{\sqrt x + 1}}{{{{\left( {\sqrt x - 1} \right)}^2}}}$

$= \frac{{1 + \sqrt x }}{{\sqrt x \left( {\sqrt x - 1} \right)}}.\frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x + 1}} = \frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x \left( {\sqrt x - 1} \right)}} = \frac{{\sqrt x - 1}}{{\sqrt x }}$

b, $P = A - 9\sqrt x = \frac{{\sqrt x - 1}}{{\sqrt x }} - 9\sqrt x = 1 - \left( {\frac{1}{{\sqrt x }} + 9\sqrt x } \right)$ với x > 0, x ≠ 1

Với x > 0, x ≠ 1, áp dụng bất đẳng thức Cauchy có: $\frac{1}{{\sqrt x }} + 9\sqrt x \ge 2.\sqrt {\frac{1}{{\sqrt x }}.9\sqrt x } = 6$

$\Rightarrow - \left( {\frac{1}{{\sqrt x }} + 9\sqrt x } \right) \le - 6 \Rightarrow 1 - \left( {\frac{1}{{\sqrt x }} + 9\sqrt x } \right) \le 1 - 6 = - 5 \Leftrightarrow P \le - 5$

Dấu “=” xảy ra $\Leftrightarrow \frac{1}{{\sqrt x }} = 9\sqrt x \Leftrightarrow x = \frac{1}{9}$ (thỏa mãn)

Vậy max $P = - 5 \Leftrightarrow x = \frac{1}{9}$

III. Bài tập vận dụng

Bài 1. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y= 1- 2|cos3x|.

A. M=3 ; m= - 1.

B. M= 1 ; m= -1.

C. M=2 ;m= -2.

D. M=0 ; m= -2.

Lời giải:.

Chọn B.

Với mọi x ta có : - 1 ≤ cos3x ≤ 1 nên 0 ≤ |cos3x| ≤ 1

⇒ 0 ≥ -2|cos3x| ≥ -2

Cách tìm Giá trị lớn nhất, nhỏ nhất của hàm số lượng giác cực hay

Bài 2: Hàm số y= 1+ 2cos²x đạt giá trị nhỏ nhất tại x= x₀. Mệnh đề nào sau đây là đúng?

A.x₀=π+k2π, kϵZ .

B.x₀=π/2+kπ, kϵZ .

C.x₀=k2π, kϵZ .

D.x₀=kπ ,kϵZ .

Lời giải:.

Chọn B.

Ta có - 1 ≤ cosx ≤ 1 ⇒ - 0 ≤ cos²x ≤ 1 ⇒ 1 ≤ 1+2cos²x ≤ 3

Do đó giá trị nhỏ nhất của hàm số bằng 1 .

Dấu ‘=’ xảy ra khi cosx=0 ⇒ x=π/2+kπ, kϵZ .

Bài 3: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y= sin2x+ 2cos2x.

A.M= 3 ;m= 0

B. M=2 ; m=0.

C. M=2 ; m= 1.

D.M= 3 ; m= 1.

Lời giải:.

Chọn C.

Ta có: y = sin² x+ 2cos²x = (sin²x+ cos²x) + cos²x = 1+ cos² x.

Do: -1 ≤ cosx ≤ 1 nên 0 ≤ cos² x ≤ 1 ⇒ 1 ≤ cos² x+1 ≤ 2

Suy ra giá trị lớn nhất của hàm số là M= 2 và giá trị nhỏ nhất của hàm số là m= 1

Bài 4: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y= 4sinx - 3

A.M= 1; m= - 7

B. M= 7; m= - 1

C. M= 3; m= - 4

D. M=4; m= -3

Lời giải

Chọn A

Ta có : - 1 ≤ sinx ≤ 1 nên - 4 ≤ 4sinx ≤ 4

Suy ra : - 7 ≤ 4sinx-3 ≤ 1

Do đó : M= 1 và m= - 7

Bài 5. Giá trị nhỏ nhất của hàm số f(x) = x⁴ - 10x² - 2 trên đoạn [0;9] bằng:

A. -2 . B. -11. C. -26 . D. -27 .

Lời giải

Ta có f'(x) = 4x³ - 20x

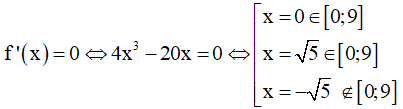
Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải

f(0) = -2; f(√5) = -27; f(9) = 5749 .

Vậy 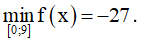Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải

Chọn D.

Bài 6. Trên đoạn [-2;1], hàm số y = x³ - 3x² - 1 đạt giá trị lớn nhất tại điểm:

A. x = -2. B. x = 0 . C. x = -1 . D. x = 1 .

Lời giải

Đặt y = f(x) = x³ – 3x² – 1

Ta có 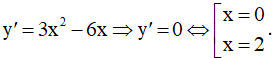Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải Ta đang xét trên đoạn [-2;1] nên loại x = 2

Ta có f(-2) = -21; f(0) = -1; f(1) = -3. Do đó giá trị lớn nhất của hàm số trên đoạn [-2;1] là –1, tại x = 0.

Chọn B.

Bài 7. Tìm giá trị lớn nhất M của hàm số 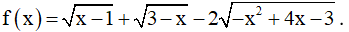Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải

A. M = 0 B. M = - √2 C. M = √2 D. 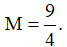Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải

Lời giải

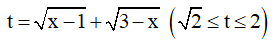
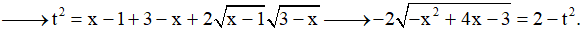
TXĐ: D = [1;3] Đặt Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải

Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải

Khi đó, bài toán trở thành ''Tìm giá trị lớn nhất của hàm số g(t) = -t² + t + 2 trên đoạn [√2;2]''.

Xét hàm số g(t) = -t² + t + 2 xác định và liên tục trên [√2;2]

Đạo hàm g'(t) = -2t + 1 < 0,∀t ∈ (√2;2) .

Suy ra hàm số g(t) nghịch biến trên đoạn [√2;2]

Do đó 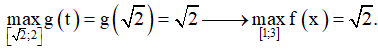Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải

Chọn C.

Ta có:

Từ phép đặt ẩn phụ 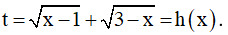Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải

Đạo hàm 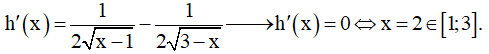Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải

Ta có 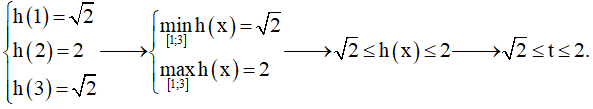Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải

Bài 8: Tìm giá trị lớn nhất nhỏ nhất của hàm số

Hướng dẫn giải

Dễ thấy nên hàm số xác định trên toàn trục số.

Gọi m là một giá trị tùy ý của hàm số, khi đó phương trình

$\begin{align} & \frac{2{{x}^{2}}+7x+23}{{{x}^{2}}+2x+10}=m \\ & \Leftrightarrow 2{{x}^{2}}+7x+23=m\left( {{x}^{2}}+2x+10 \right) \\ & \Leftrightarrow \left( m-2 \right){{x}^{2}}+\left( 2m-7 \right)x+10m-23=0 \\ \end{align}$

Ta xét hai trường hợp sau:

TH1: Nếu phương trình trở thành vậy phương trình có nghiệm khi

TH2: Nếu khi đó phương trình bậc 2 có nghiệm khi và chỉ khi:

$\begin{align} & \Delta ={{\left( 2m-7 \right)}^{2}}-4\left( m-2 \right)\left( 10m-23 \right)\ge 0 \\ & \Leftrightarrow -36m+144m-135\ge 0 \\ & \Rightarrow \frac{3}{2}\le m\le \frac{5}{2}\ne 2 \\ & \Rightarrow \max f\left( x \right)=\frac{5}{2},\min f\left( x \right)=\frac{3}{2} \\ \end{align}$

Bài 9. Tìm giá trị lớn nhất M của hàm số f(x) = |-x² - 4x + 5| trên đoạn [-6;6] .

A. M = 0 B. M = 9 C. M = 55 D. M = 110

Lời giải

Xét hàm số g(x) = -x² - 4x + 5 liên tục trên đoạn [-6;6].

Đạo hàm g'(x) = -2x - 4 → g'(x) = 0 ⇔ x = -2 ∈ [-6;6]

Lại có 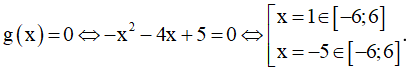Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải

Ta có

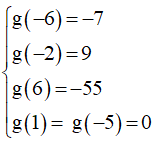
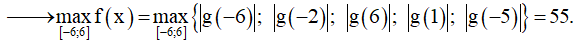
Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải

Chọn C.

Lưu ý: Hàm trị tuyệt đối không âm.

Bài 10. Tìm giá trị nhỏ nhất m của hàm số 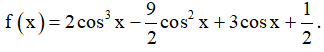Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải

A. m = -24 B. m = -12 C. m = -9 D. m = 1

Lời giải

Đặt t = cosx (-1 ≤ t ≤ 1)

Khi đó, bài toán trở thành ''Tìm giá trị nhỏ nhất của hàm số 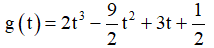Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải trên đoạn [-1;1] ''.

Đạo hàm 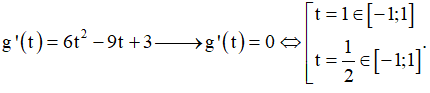Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải

Ta có 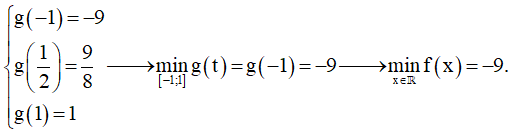Các dạng bài tập về giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải

Chọn C.

Xem thêm các dạng câu hỏi và bài tập liên quan khác:

30 bài tập Tìm Giá trị lớn nhất, nhỏ nhất của hàm số lượng giác cực hay 2024

30 Bài tập tìm giá trị lớn nhất của biểu thức (2024) có đáp án

50 bài tập về giá trị lớn nhất, giá trị nhỏ nhất của phân thức (có đáp án 2024)

30 Bài tập tìm giá trị nhỏ nhất của biểu thức (2024) có đáp án

20 bài tập Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức chứa căn (2024) mới nhất, có đáp án

Được cập nhật 24/05/2024 428 lượt xem

Bởi Trang Quỳnh

Chủ đề: Tổng hợp các dạng bài tập Toán Các công thức tính min max 9 10 11 12

Bình luận (0)

Đăng nhập để có thể bình luận

Chưa có bình luận nào. Bạn hãy là người đầu tiên cho tôi biết ý kiến!

Bài viết cùng chủ đề

Tổng hợp các dạng bài tập Toán

30 bài tập các dạng phương trình hình học 2024 (có đáp án)

1900.edu.vn xin giới thiệu bài tập và tóm tắt lý thuyết Toán: các dạng phương trình hình học hay, chi tiết cùng với bài tập trắc nghiệm chọn lọc có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9. Mời các bạn đón xem:

446 3 tháng trước

Tổng hợp các dạng bài tập Toán

30 bài tập các dạng lượng giác 2024 (có đáp án)

1900.edu.vn xin giới thiệu bài tập và tóm tắt lý thuyết Toán: các dạng lượng giác hay, chi tiết cùng với bài tập trắc nghiệm chọn lọc có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12. Mời các bạn đón xem:

478 3 tháng trước

Tổng hợp các dạng bài tập Toán

30 bài tập các dạng đồ thị phương trình 2024 (có đáp án)

1900.edu.vn xin giới thiệu bài tập và tóm tắt lý thuyết Toán: các dạng đồ thị phương trình hay, chi tiết cùng với bài tập trắc nghiệm chọn lọc có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12. Mời các bạn đón xem:

467 3 tháng trước

30 bài tập các công thức tính min max 9 10 11 12 2024 (có đáp án)

I. Lý thuyết

II. Ví dụ minh họa

III. Bài tập vận dụng

Bình luận (0)

Bài viết cùng chủ đề

30 bài tập các dạng phương trình hình học 2024 (có đáp án)

30 bài tập các dạng lượng giác 2024 (có đáp án)

30 bài tập các dạng đồ thị phương trình 2024 (có đáp án)

Nội dung bài viết