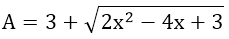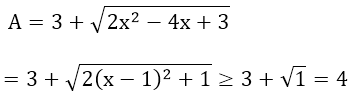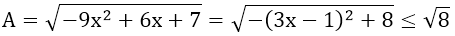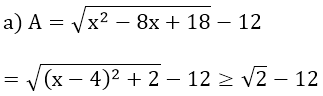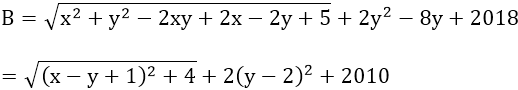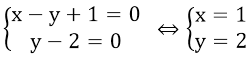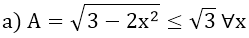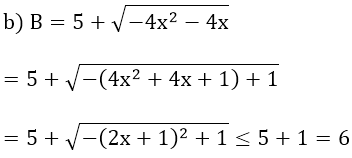30 Bài tập tìm giá trị nhỏ nhất của biểu thức (2024) có đáp án

1900.edu.vn xin giới thiệu 30 Bài tập tìm giá trị nhỏ nhất của biểu thức hay, chi tiết nhất sẽ giúp các bạn học sinh ôn tập và củng cố kiến thức đã học, tự luyện tập nhằm học tốt môn Toán 9 tốt hơn. Mời các em tham khảo:

Bài tập tìm giá trị nhỏ nhất của biểu thức

1. Phương pháp giải

a. Biến đổi biểu thức

Bước 1: Biến đổi biểu thức về dạng tổng hoặc hiệu của một số không âm với hằng số.

$\left[ {\begin{array}{*{20}{c}} {GTNN:\sqrt {{A^2} + m} \geqslant \sqrt m } \\ {GTLN:\sqrt {m - {A^2}} \leqslant \sqrt m } \end{array};\left( {m \geqslant 0} \right)} \right.$

Bước 2: Thực hiện tìm giá trị lớn nhất, nhỏ nhất

b. Chứng minh biểu thức luôn dương hoặc luôn âm

Phương pháp:

- Để chứng minh biểu thức A luôn dương ta cần chỉ ra: $A = {A_1}^2 + k;\left( {k > 0} \right)$

- Để chứng minh biểu thức A luôn âm ta cần chỉ ra: $A =- {A_1}^2 - k;\left( {k > 0} \right)$

c. Sử dụng bất đẳng thức Cauchy

Cho hai số a, b không âm ta có:

$a + b \geqslant 2\sqrt {ab}$

Dấu bằng xảy ra khi và chỉ khi a = b

d. Sử dụng bất đẳng thức chứa dấu giá trị tuyệt đối

$\left| a \right| + \left| b \right| \geqslant \left| {a + b} \right|$

Dấu “=” xảy ra khi và chỉ khi tích $a.b \geqslant 0$

2. Ví dụ minh họa

Ví dụ 1: Tìm giá trị nhỏ nhất của biểu thức:

Chuyên đề Toán lớp 9 | Chuyên đề Lý thuyết và Bài tập Đại số và Hình học 9 có đáp án

Lời giải:

Chuyên đề Toán lớp 9 | Chuyên đề Lý thuyết và Bài tập Đại số và Hình học 9 có đáp án

Vậy giá trị nhỏ nhất của biểu thức A là 4, đạt được khi x = 1

Ví dụ 2: Tìm giá trị lớn nhất của biểu thức sau:

Chuyên đề Toán lớp 9 | Chuyên đề Lý thuyết và Bài tập Đại số và Hình học 9 có đáp án

Lời giải:

Dấu bằng xảy ra khi 3x - 1 = 0 ⇔ x = 1/3.

Vậy giá trị lớn nhất của A là √8, đạt được khi x = 1/3.

3. Bài tập vận dụng

Bài 1: Tìm giá trị lớn nhất của biểu thức:

a. $E = \frac{1}{{\sqrt x + 1}}$

b. $D = \frac{{\sqrt x + 3}}{{\sqrt x + 2}}$

Gợi ý đáp án

a. Điều kiện xác định $x \geqslant 0$

Do $\sqrt x \geqslant 0 \Rightarrow \sqrt x + 1 \geqslant 1 \Rightarrow \frac{1}{{\sqrt x + 1}} \leqslant 1 \Rightarrow \max A = 1$

Dấu “=” xảy ra khi và chỉ khi x = 0

Vậy GTLN của E bằng 1 khi x = 0

b. Điều kiện xác định $x \geqslant 0$

$D = \frac{{\sqrt x + 3}}{{\sqrt x + 2}} = 1 + \frac{1}{{\sqrt x + 2}}$

Do $\sqrt x \geqslant 0 \Rightarrow \sqrt x + 2 \geqslant 2 \Rightarrow \frac{1}{{\sqrt x + 2}} \leqslant \frac{1}{2} \Rightarrow \max A = 1 + \frac{1}{2} = \frac{3}{2}$

Dấu “=” xảy ra khi và chỉ khi x = 0

Vậy GTLN của D bằng 3/2 khi x = 0

Bài 2: Tìm giá trị lớn nhất của biểu thức $A = \frac{1}{{x - \sqrt x + 1}}$

Gợi ý đáp án

Điều kiện xác định x ≥ 0

Để A đạt giá trị lớn nhất thì $x - \sqrt x + 1$ đạt giá trị nhỏ nhất

Có $x - \sqrt x + 1 = x - 2.\frac{1}{2}.\sqrt x + \frac{1}{4} - \frac{1}{4} + 1 = {\left( {\sqrt x - \frac{1}{2}} \right)^2} + \frac{3}{4}$

Lại có ${\left( {\sqrt x - \frac{1}{2}} \right)^2} \ge 0\forall x \ge 0 \Rightarrow {\left( {\sqrt x - \frac{1}{2}} \right)^2} + \frac{3}{4} \ge \frac{3}{4}\forall x \ge 0$

Dấu “=” xảy ra $\Leftrightarrow \sqrt x = \frac{1}{2} \Leftrightarrow x = \frac{1}{4}$

Min $x - \sqrt x + 1 = \frac{3}{4} \Leftrightarrow x = \frac{1}{4}$

Vậy Max $A = \frac{4}{3} \Leftrightarrow x = \frac{1}{4}$

Bài 3: Tìm giá trị lớn nhất của biểu thức: $Q = {x^2}\sqrt {9 - {x^2}}$

Gợi ý đáp án

Điều kiện xác định: $x \in \left[ { - 3;3} \right]$

Ta có:

$\begin{matrix} {Q^2} = {x^4}\left( {9 - {x^2}} \right) \hfill \\ {Q^2} = 4.\dfrac{{{x^2}}}{2}.\dfrac{{{x^2}}}{2}\left( {9 - {x^2}} \right) \hfill \\ \end{matrix}$

Áp dụng bất đẳng thức Cauchy ta có:

$\begin{matrix} {Q^2} \leqslant 4.\dfrac{{{{\left( {\dfrac{{{x^2}}}{2} + \dfrac{{{x^2}}}{2} + \left( {9 - {x^2}} \right)} \right)}^3}}}{{27}} = 4.27 \hfill \\ \Rightarrow Q \leqslant 6\sqrt 3 \hfill \\ \Rightarrow \max Q = 6\sqrt 3 \hfill \\ \end{matrix}$

Dấu “=” xảy ra khi và chỉ khi $x = \pm \sqrt 6$

Bài 4: Cho biểu thức $A = \left( {\frac{1}{{x - \sqrt x }} + \frac{1}{{\sqrt x - 1}}} \right):\frac{{\sqrt x + 1}}{{{{\left( {\sqrt x - 1} \right)}^2}}}$

a, Rút gọn A

b, Tìm giá trị lớn nhất của biểu thức $P = A - 9\sqrt x$

Gợi ý đáp án

Cách 1

a, $A = \left( {\frac{1}{{x - \sqrt x }} + \frac{1}{{\sqrt x - 1}}} \right):\frac{{\sqrt x + 1}}{{{{\left( {\sqrt x - 1} \right)}^2}}}$ với x > 0, x ≠ 1

$= \left( {\frac{1}{{\sqrt x \left( {\sqrt x - 1} \right)}} + \frac{1}{{\sqrt x - 1}}} \right):\frac{{\sqrt x + 1}}{{{{\left( {\sqrt x - 1} \right)}^2}}}$

$= \frac{{1 + \sqrt x }}{{\sqrt x \left( {\sqrt x - 1} \right)}}.\frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x + 1}} = \frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x \left( {\sqrt x - 1} \right)}} = \frac{{\sqrt x - 1}}{{\sqrt x }}$

b, $P = A - 9\sqrt x = \frac{{\sqrt x - 1}}{{\sqrt x }} - 9\sqrt x = 1 - \left( {\frac{1}{{\sqrt x }} + 9\sqrt x } \right)$ với x > 0, x ≠ 1

Với x > 0, x ≠ 1, áp dụng bất đẳng thức Cauchy có: $\frac{1}{{\sqrt x }} + 9\sqrt x \ge 2.\sqrt {\frac{1}{{\sqrt x }}.9\sqrt x } = 6$

$\Rightarrow - \left( {\frac{1}{{\sqrt x }} + 9\sqrt x } \right) \le - 6 \Rightarrow 1 - \left( {\frac{1}{{\sqrt x }} + 9\sqrt x } \right) \le 1 - 6 = - 5 \Leftrightarrow P \le - 5$

Dấu “=” xảy ra $\Leftrightarrow \frac{1}{{\sqrt x }} = 9\sqrt x \Leftrightarrow x = \frac{1}{9}$ (thỏa mãn)

Vậy max $P = - 5 \Leftrightarrow x = \frac{1}{9}$

Cách 2: Thêm bớt rồi dùng bất đẳng thức Cauchy hoặc đánh giá dựa vào điều kiện đề bài.

Với điều kiện x > 0 và x ≠ 1 ta có:

$P = A - 9\sqrt x = \frac{{\sqrt x - 1}}{{\sqrt x }} - 9\sqrt x = 1 - \frac{1}{{\sqrt x }} - 9\sqrt x = 1 - \left( {9\sqrt x + \frac{1}{{\sqrt x }}} \right)$

Theo bất đẳng thức Cauchy ra có:

$9\sqrt x + \frac{1}{{\sqrt x }} \geqslant 2\sqrt {9\sqrt x .\frac{1}{{\sqrt x }}} \Leftrightarrow 9\sqrt x + \frac{1}{{\sqrt x }} \geqslant 6$

Như vậy P ≤ -5

Đẳng thức xảy ra khi và chỉ khi $9\sqrt x = \frac{1}{{\sqrt x }}$ hay x = 1/9

Vậy giá trị lớn nhất của P là -5 khi và chỉ khi x = 1/9

Cách 3: Dùng miền giá trị để đánh giá

Với điều kiện x > 0 và x ≠ 1 ta có:

$P = A - 9\sqrt x = \frac{{\sqrt x - 1}}{{\sqrt x }} - 9\sqrt x = 1 - \frac{1}{{\sqrt x }} - 9\sqrt x$ (P < 1)

$\begin{matrix} \Leftrightarrow P\sqrt x = \sqrt x - 1 - 9x \hfill \\ \Leftrightarrow 9x + \left( {P - 1} \right)\sqrt x + 1 = 0 \hfill \\ \Leftrightarrow 9{\left( {\sqrt x } \right)^2} + \left( {P - 1} \right)\sqrt x + 1 = 0\left( * \right) \hfill \\ \end{matrix}$

Để tổn tại P thì phương trình (*) phải có nghiệm, tức là:

∆ = (P - 1)² - 36 ≥ 0 ⇔ (P - 1)² ≥ 36 ⇔ P - 1 ≤ -6 (Do P < 1) ⇔ P ≤ -5

Như vậy P ≤ -5 khi $\sqrt x = \frac{{ - \left( {P - 1} \right)}}{{2.9}} = \frac{{ - \left( { - 5 - 1} \right)}}{{2.9}} = \frac{1}{3} \Rightarrow x = \frac{1}{9}$

Vậy giá trị lớn nhất của P là -5 khi và chỉ khi x = 1/9

Bài 5: Cho biểu thức $A = \left( {\frac{{\sqrt x }}{{2 - \sqrt x }} + \frac{{\sqrt x }}{{2 + \sqrt x }}} \right) - \frac{{6 + \sqrt x }}{{4 - x}}$ với x ≥ 0, x ≠ 4

a, Rút gọn A

b, Tìm giá trị nhỏ nhất của A

Gợi ý đáp án

a, $A = \left( {\frac{{\sqrt x }}{{2 - \sqrt x }} + \frac{{\sqrt x }}{{2 + \sqrt x }}} \right) - \frac{{6 + \sqrt x }}{{4 - x}}$ với x ≥ 0, x ≠ 4

$= \frac{{\sqrt x \left( {2 + \sqrt x } \right) + \sqrt x \left( {2 - \sqrt x } \right)}}{{\left( {2 + \sqrt x } \right)\left( {2 - \sqrt x } \right)}} - \frac{{6 + \sqrt x }}{{\left( {2 + \sqrt x } \right)\left( {2 - \sqrt x } \right)}}$

$= \frac{{2\sqrt x + x + 2\sqrt x - x}}{{\left( {2 + \sqrt x } \right)\left( {2 - \sqrt x } \right)}} - \frac{{6 + \sqrt x }}{{\left( {2 + \sqrt x } \right)\left( {2 - \sqrt x } \right)}}$

$= \frac{{4\sqrt x - 6 - \sqrt x }}{{\left( {2 + \sqrt x } \right)\left( {2 - \sqrt x } \right)}} = \frac{{3\sqrt x - 6}}{{\left( {2 + \sqrt x } \right)\left( {2 - \sqrt x } \right)}}$

$= \frac{{3.\left( {\sqrt x - 2} \right)}}{{\left( {2 + \sqrt x } \right)\left( {2 - \sqrt x } \right)}} = \frac{{ - 3}}{{2 + \sqrt x }}$

b, Có

Dấu “=” xảy ra ⇔ x = 0

Vậy min $A = \frac{{ - 3}}{2} \Leftrightarrow x = 0$

Bài 6:

Cho hai số thực a,b # 0 thỏa mãn $2{a^2} + \dfrac{{{b^2}}}{4} + \dfrac{1}{{{a^2}}} = 4$ . Tìm GTLN, GTNN của $S = ab + 2017$

Gợi ý đáp án

Ta giả thiết ta có:

$\begin{array}{l} 4 = \left( {{a^2} + \dfrac{1}{{{a^2}}} - 2} \right) + \left( {{a^2} + \dfrac{{{b^2}}}{4} - ab} \right) + ab + 2\\ = {\left( {a - \frac{1}{a}} \right)^2} + {\left( {a - \dfrac{b}{2}} \right)^2} + ab + 2\\ \Rightarrow ab + 2 \le 4 \Rightarrow ab + 2017 \le 2019 \Rightarrow S \le 2019 \end{array}$$

Mặt khác

$\begin{array}{l} 4 = \left( {{a^2} + \dfrac{1}{{{a^2}}} - 2} \right) + \left( {{a^2} + \dfrac{{{b^2}}}{4} - ab} \right) - ab + 2\\ = {\left( {a - \dfrac{1}{a}} \right)^2} + {\left( {a - \dfrac{b}{2}} \right)^2} - ab + 2\\ \Rightarrow - ab + 2 \le 4 \Rightarrow ab \ge 2 \Rightarrow ab + 2017 \ge 2015 \Rightarrow S \ge 2015 \end{array}$

Bài 7: Cho hai số x,y khác 0 thỏa mãn ${x^2} + \dfrac{8}{{{x^2}}} + \dfrac{{{y^2}}}{8} = 8$ . Tìm min, max của A= xy+2024

Gợi ý đáp án

Từ giả thiết ta có:

$\begin{array}{l} 8 = {x^2} + \dfrac{8}{{{x^2}}} + \dfrac{{{y^2}}}{8} \Rightarrow 16 = 2{x^2} + \dfrac{{16}}{{{x^2}}} + \dfrac{{{y^2}}}{4}\\ = \left( {{x^2} + \dfrac{{16}}{{{x^2}}} - 8} \right) + \left( {{x^2} + xy + \dfrac{{{y^2}}}{4}} \right) - xy + 8\\ \Rightarrow 8 = {\left( {x - \dfrac{4}{x}} \right)^2} + {\left( {x + \dfrac{y}{2}} \right)^2} - xy + 8 \le 16 \Rightarrow xy \ge - 8\\ \Rightarrow A = xy + 2024 \ge 2016 \end{array}$

Mặt khác

$\begin{array}{l} 16 = \left( {{x^2} + \dfrac{{16}}{{{x^2}}} - 8} \right) + \left( {{x^2} + xy + \dfrac{{{y^2}}}{4}} \right) + xy + 8\\ = {\left( {x - \dfrac{4}{x}} \right)^2} + {\left( {x + \dfrac{y}{2}} \right)^2} + xy - 8 \Rightarrow xy - 8 \le 16 \Rightarrow xy \le 8 \Rightarrow S = xy + 2024 \le 2032 \end{array}$

Bài 8: Cho x, y khác 0 biết $8{x^2} + {y^2} + \dfrac{1}{{4{x^2}}} = 4$ . Tìm x,y để B=xy đạt GTLN, GTNN

Hướng dẫn giải

Ta có

$\begin{array}{l} 4 = 8{x^2} + {y^2} + \dfrac{1}{{4{x^2}}} = \left( {4{x^2} - 2 + \dfrac{1}{{4{x^2}}}} \right) + \left( {4{x^2} + {y^2} - 4xy} \right) + 4xy + 2\\ 4 = {\left( {2x - \dfrac{1}{{2x}}} \right)^2} + {\left( {2x - y} \right)^2} + 4xy + 2 \Rightarrow 4xy + 2 \le 4 \Rightarrow B = xy \le \dfrac{1}{2} \end{array}$

Mặt khác

$4 = {\left( {2x - \dfrac{1}{{2x}}} \right)^2} + {\left( {2x + y} \right)^2} - 4xy + 2 \Rightarrow - 4xy + 2 \le 4 \Rightarrow B = xy \ge - \dfrac{1}{2}$

Bài 9:

Chuyên đề Toán lớp 9 | Chuyên đề Lý thuyết và Bài tập Đại số và Hình học 9 có đáp án

Vậy giá trị nhỏ nhất của biểu thức A là √2 - 12, đạt được khi x = 4.

Chuyên đề Toán lớp 9 | Chuyên đề Lý thuyết và Bài tập Đại số và Hình học 9 có đáp án

⇒ B ≥ √4 + 2010 = 2012

Vậy giá trị nhỏ nhất của B là 2012, đạt được khi Chuyên đề Toán lớp 9 | Chuyên đề Lý thuyết và Bài tập Đại số và Hình học 9 có đáp án

Bài 10:

Chuyên đề Toán lớp 9 | Chuyên đề Lý thuyết và Bài tập Đại số và Hình học 9 có đáp án

Dấu bằng xảy ra khi 2x² = 0 ⇔ x = 0.

Vậy giá trị lớn nhất của A là √3 khi x = 0

Chuyên đề Toán lớp 9 | Chuyên đề Lý thuyết và Bài tập Đại số và Hình học 9 có đáp án

Dấu bằng xảy ra khi 2x + 1 = 0 ⇔ x = -1/2

Vậy giá trị lớn nhất của B là 6 khi x = -1/2.

Xem thêm các dạng bài tập Toán liên quan khác:

20 bài tập Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức chứa căn (2024) mới nhất, có đáp án

30 bài tập Tìm Giá trị lớn nhất, nhỏ nhất của hàm số lượng giác cực hay 2024

20 Bài tập Ứng dụng của hàm số bậc hai chứng minh bất đẳng thức và tìm giá trị nhỏ nhất, lớn nhất (2024) cực hay, có đáp án

60 Bài tập về Giá trị lớn nhất và giá trị nhỏ nhất của hàm số (có đáp án năm 2024)

50 bài tập về giá trị lớn nhất, giá trị nhỏ nhất của phân thức (có đáp án 2024)

Được cập nhật 12/12/2023 503 lượt xem

Bởi Trần Trung

Chủ đề: Tổng hợp các dạng bài tập Toán toán 9 tìm giá trị nhỏ nhất của biểu thức

Bình luận (0)

Đăng nhập để có thể bình luận

Chưa có bình luận nào. Bạn hãy là người đầu tiên cho tôi biết ý kiến!

Bài viết cùng chủ đề

Tổng hợp các dạng bài tập Toán

30 bài tập các dạng phương trình hình học 2024 (có đáp án)

1900.edu.vn xin giới thiệu bài tập và tóm tắt lý thuyết Toán: các dạng phương trình hình học hay, chi tiết cùng với bài tập trắc nghiệm chọn lọc có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9. Mời các bạn đón xem:

510 5 tháng trước

Tổng hợp các dạng bài tập Toán

30 bài tập các dạng lượng giác 2024 (có đáp án)

1900.edu.vn xin giới thiệu bài tập và tóm tắt lý thuyết Toán: các dạng lượng giác hay, chi tiết cùng với bài tập trắc nghiệm chọn lọc có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12. Mời các bạn đón xem:

577 5 tháng trước

Tổng hợp các dạng bài tập Toán

30 bài tập các dạng đồ thị phương trình 2024 (có đáp án)

1900.edu.vn xin giới thiệu bài tập và tóm tắt lý thuyết Toán: các dạng đồ thị phương trình hay, chi tiết cùng với bài tập trắc nghiệm chọn lọc có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12. Mời các bạn đón xem:

566 5 tháng trước

30 Bài tập tìm giá trị nhỏ nhất của biểu thức (2024) có đáp án

1900.edu.vn xin giới thiệu 30 Bài tập tìm giá trị nhỏ nhất của biểu thức hay, chi tiết nhất sẽ giúp các bạn học sinh ôn tập và củng cố kiến thức đã học, tự luyện tập nhằm học tốt môn Toán 9 tốt hơn. Mời các em tham khảo:

1. Phương pháp giải

2. Ví dụ minh họa

3. Bài tập vận dụng

Bình luận (0)

Bài viết cùng chủ đề

30 bài tập các dạng phương trình hình học 2024 (có đáp án)

30 bài tập các dạng lượng giác 2024 (có đáp án)

30 bài tập các dạng đồ thị phương trình 2024 (có đáp án)

Nội dung bài viết