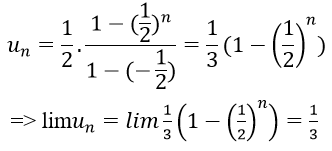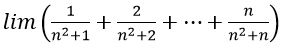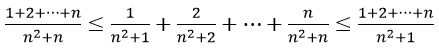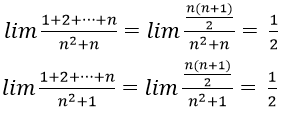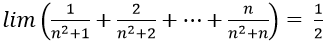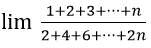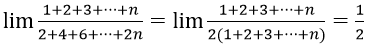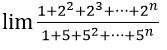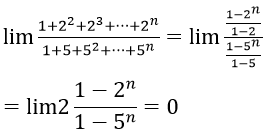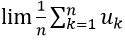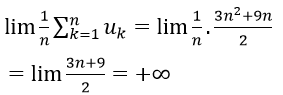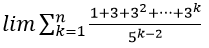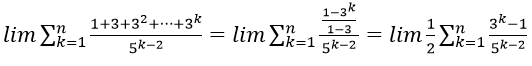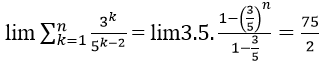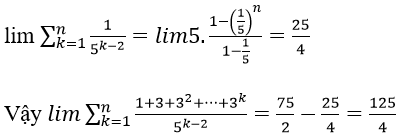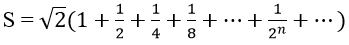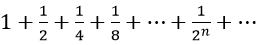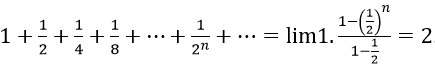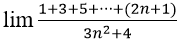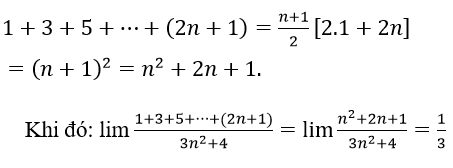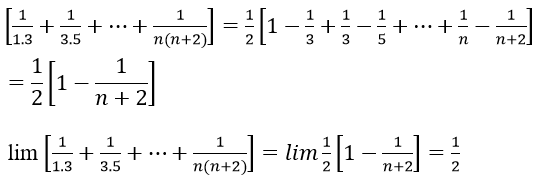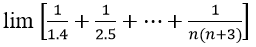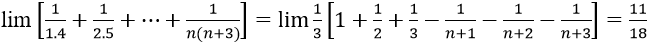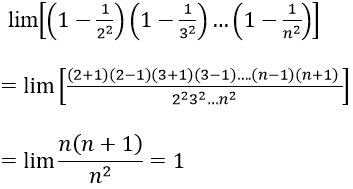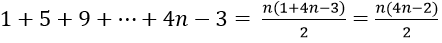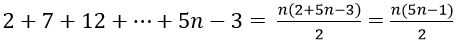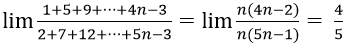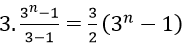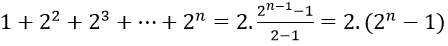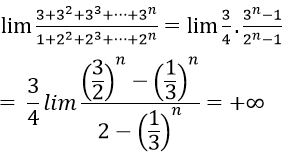20 Bài tập Cách tính giới hạn của dãy số (2024) cực hay, có đáp án

Cách tính giới hạn của dãy số cực hay

Lý thuyết

1. Dãy số có giới hạn 0

Ta nói rằng dãy số (u_n) có giới hạn là 0 khi n dần tới dương vô cực, nếu với mỗi số dương nhỏ tùy ý cho trước, mọi số hạng của dãy số kể từ một số hạng nào đó trở đi, |u_n| nhỏ hơn số dương đó.

Kí hiệu: $\underset{n\to \infty }{\lim }{u}_n=0$ hay lim u_n = 0 hay $u_n\to 0$ khi $n\to +\infty$.

2. Dãy số có giới hạn hữu hạn

Ta nói rằng dãy số (u_n) có giới hạn là số thực L nếu lim (u_n – L) = 0

Kí hiệu: $\underset{n\to \infty }{\lim }{u}_n=L$ hay lim u_n = L hay $u_n\to L$ khi $n\to +\infty$.

3. Dãy số có giới hạn vô cực

Dãy số (u_n) có giới hạn là $+\infty$ khi $n\to +\infty$, nếu u_n có thể lớn hơn một số dương bất kì kể từ một số hạng nào đó trở đi.

Ký hiệu: $\lim u_n=+\infty$ hoặc $u_n\to +\infty khin\to +\infty$

Dãy số (u_n) có giới hạn là $-\infty$ khi $n\to +\infty$, nếu $\lim \left(-u_n\right)=+\infty$

Ký hiệu: $\lim u_n=-\infty$ hoặc $u_n\to -\infty khin\to +\infty$

4. Một vài giới hạn đặc biệt

$\lim u_n=0\iff \lim \left|u_n\right|=0$

$\lim \frac{1}{n}=0; \lim \frac{1}{n^k}=0,\left(k>0,k\in {\mathbb{N}}^{*}\right)$

$\lim n^k=+\infty ,\left(k>0,k\in {\mathbb{N}}^{*}\right)$

$\lim q^n=\left\{\begin{array}{l}0 khi\left|q\right|<1\\ +\infty khiq>1\end{array}\right.$

5. Định lý về giới hạn hữu hạn

* Nếu lim u_n = a và lim v_n = b và c là hằng số. Khi đó ta có :

lim(u_n + v_n) = a + b

lim(u_n - v_n) = a - b

lim(u_n v_n) = a.b

$\lim \frac{u_n}{v_n}=\frac{a}{b},\left(b\ne 0\right)$

lim(cu_n ) = c.a

lim|u_n | = |a|

$\lim \sqrt[3]{u_n}=\sqrt[3]{a}$

Nếu $u_n\ge 0$ với mọi n thì $a\ge 0$ và $\lim \sqrt{u_n}=\sqrt{a}$.

* Định lí kẹp: Cho ba dãy số (v_n); (u_n) và (w_n):

Nếu $\left\{\begin{array}{l}\left(v_n\right)\le \left(u_n\right)\le \left({\text{w}}_n\right),\forall n\in N^{*}\\ \lim v_n=\lim w_n=a\end{array}\right.$ thì lim u_n = a.

Hệ quả: Cho hai dãy số (u_n) và (v_n):

Nếu $\left\{\begin{array}{l}\left|u_n\right|\le v_n,\forall n\in N^{*}\\ \lim v_n=0\end{array}\right.$ thì lim u_n = 0.

6. Một vài quy tắc tìm giới hạn vô cực

* Quy tắc tìm giới hạn tích lim (u_nv_n)

Nếu $\lim u_n=L\ne 0,\lim v_n=+\infty (hay-\infty )$. Khi đó: lim (u_nv_n)

* Quy tắc tìm giới hạn thương

7. Tổng cấp số nhân lùi vô hạn

Xét cấp số nhân vô hạn u₁; u₁q; u₁q²; … u₁qⁿ; … có công bội |q| < 1 được gọi là cấp số nhân lùi vô hạn.

Tổng của cấp số nhân lùi vô hạn là: $S=u_1+u_{1}q+u_1{q}^2+\mathrm{....}=\frac{u_1}{1-q}\left(\left|q\right|<1\right)$

Phương pháp giải

- Ta quan sát, phân tích những đặc điểm của dãy số đề bài cho, từ đó rút ra công thu gọn cho tổng đó (có thể dùng công thức tính tổng của cấp số cộng hoặc cấp số nhân) hoặc biến đổi đại số để giảm bớt những hạng tử trong tổng,…

- Dùng các quy tắc tính giới hạn của dãy số để tính giới hạn của tổng đã cho sau khi đã thu gọn.

 Ví dụ minh họa

Ví dụ 1: Cho dãy số (u_n) với 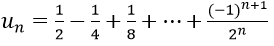. Tính lim u_n

Hướng dẫn:

u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 1/2 và q = (-1)/2.

Do đó

Ví dụ 2: Tính lim 

Hướng dẫn:

Vậy 

Ví dụ 3: Tính 

Hướng dẫn:

Ta có

Mà

Vậy 

Ví dụ 4: Tính 

Hướng dẫn:

Ví dụ 5: Tính 

Hướng dẫn:

Ví dụ 6: Cho dãy số (u_n). Biết 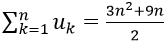 với mọi n ≥ 1. Tìm 

Hướng dẫn:

Ví dụ 7: Tính 

Hướng dẫn:

Khi đó 

Bài tập vận dụng (có đáp án)

Bài 1: Tìm giá trị đúng của 

A. √2 + 1.             B. 2.             C. 2√2.             D. 1/2.

Lời giải:

Đáp án: C

Ta có:

là tổng của cấp số nhân lùi vô hạn với số hạng đầu là 1 và công bội là 1/2. Khi đó:

Vậy S = 2√2.

Chọn đáp án C.

Bài 2: Tính giới hạn: 

A. 0            B. 1/3            C. 2/3            D. 1

Lời giải:

Đáp án: B

Ta có:

Đáp án B.

Bài 3: Tính giới hạn: 

A. 0             B. 1            C. 3/2              D. Không có giới hạn

Lời giải:

Đáp án: B

Ta có:

Khi đó 

Đáp án B

Bài 4: Tính giới hạn: 

A. 1            B. 0            C. 2/3            D. 2

Lời giải:

Đáp án: D

Ta có:

Khi đó

Chọn đáp án D.

Bài 5: Tính giới hạn: 

A. 1/2            B. 1            C. 0            D. 2/3

Lời giải:

Đáp án: A

Ta có:

Đáp án A

Bài 6: Tính giới hạn: 

A. 11/18            B. 2            C. 1            D. 3/2

Lời giải:

Đáp án: A

Bài 7: Tính giới hạn: 

A. 1            B. 1/2            C. 1/4            D. 3/2

Lời giải:

Đáp án: A

Ta có:

Đáp án A

Bài 8: Cho dãy số (u_n) với 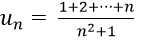. Mệnh đề nào sau đây là mệnh đề đúng?

A. lim⁡u_n = 0

B. lim⁡u_n = 1/2

C. lim⁡u_n = 1

D. Dãy số (u_n) không có giới hạn khi n → +∞

Lời giải:

Đáp án: B

Ta có:

Do đó 

Đáp án B

Bài 9: 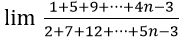 bằng:

Lời giải:

Đáp án: A

Chọn A.

Từ thức là tổng của n số hạng đầu tiên của cấp số cộng (u_n) với n = 1, u_n = 4n-3 và công bội d = 4

Do đó 

Tương tự ta có

Vậy 

Bài 10: 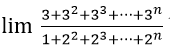 bằng:

+∞            B. 3            C. 3/2            D. 2/3

Lời giải:

Đáp án: A

Chọn A

Ta có từ thức là tổng n số hạng đầu tiên của cấp số nhân (u_n) với u_{i = 3} và q = 3

Do đó 3 + 3² + 3³ + ⋯ + 3ⁿ = 

Mẫu thức là tổng của n+1 số hạng đầu tiên của cấp số nhân (v_n) với v_n = 1 và q = 2.

Do đó 

Vậy

Xem thêm các dạng bài tập liên quan khác:

70 Bài tập về giới hạn của hàm số (có đáp án năm 2024)

30 Bài tập Tìm giới hạn của dãy số bằng định nghĩa (2024) cực hay, có đáp án

20 Bài tập Cách tính giới hạn của hàm số có chứa trị tuyệt đối (2024) cực hay, có đáp án chi tiết

20 Bài tập Cách tính giới hạn của dãy số có chứa căn thức (2024) cực hay, có đáp án chi tiết

500 Bài tập Toán 11 chương 4: Giới hạn (có đáp án năm 2024)