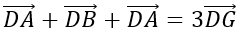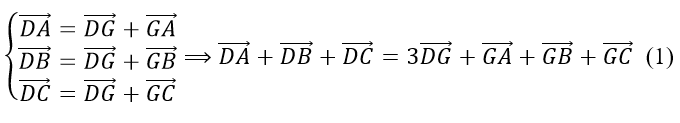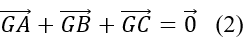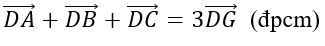Tính chất trọng tâm tứ diện
I. Lý thuyết
Khái niệm trọng tâm của tứ diện
Trọng tâm của tứ diện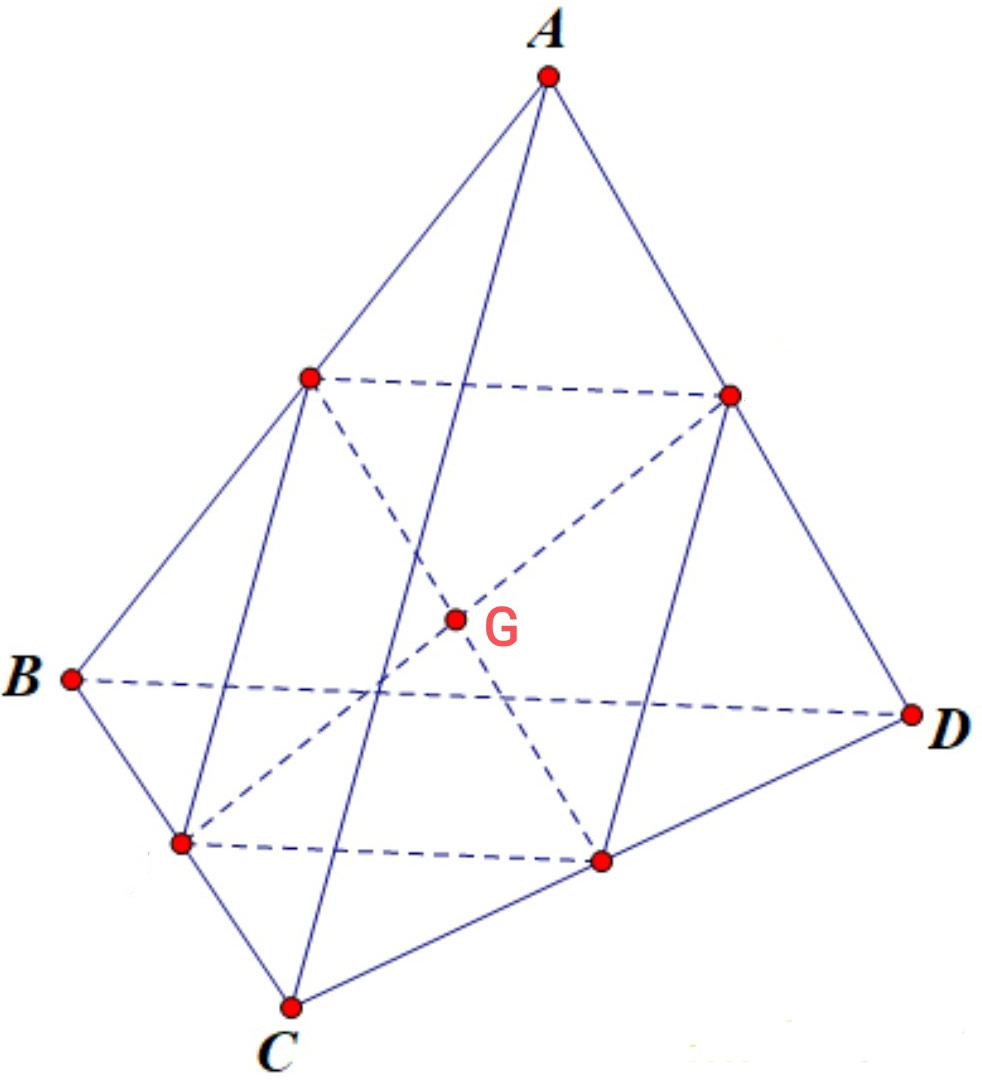
Trước hết ta xét bài toán sau đây.
Bài toán
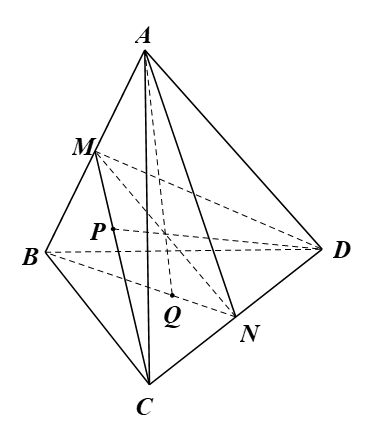
Cho tứ diện ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các đoạn thẳng AC, BD, AB, CD, AD, BC. Chứng minh rằng các đoạn thẳng MN, PQ, RS đồng quy tại trung điểm G của mỗi đoạn.

Khái niệm trọng tâm của tứ diện
Điểm G trong bài toán trên được gọi là trọng tâm của tứ diện ABCD.
Ta có thể nói: Trọng tâm của một tứ diện là trung điểm của đoạn nối các trung điểm của cặp cạnh đối diện.
Tính chất trọng tâm tứ diện
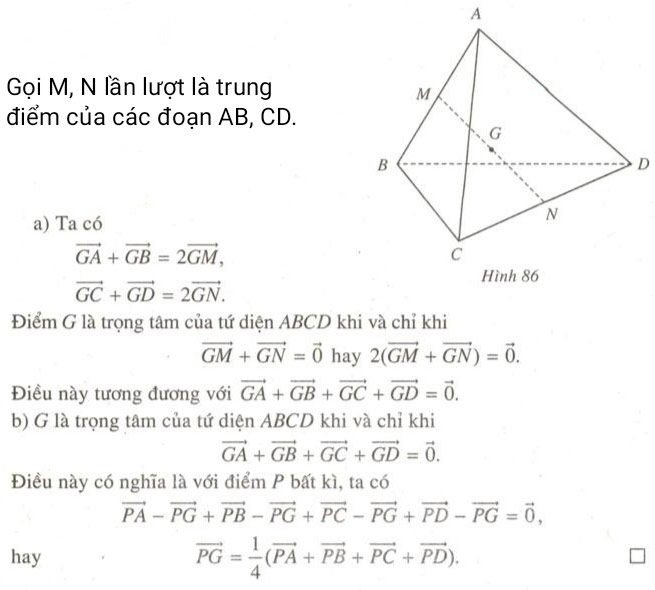
Một số sách dùng đẳng thức vectơ ở mục a) sau đây để định nghĩa trọng tâm của tứ diện.

Chứng minh
II.Bài tập
Bài 1:

Giải
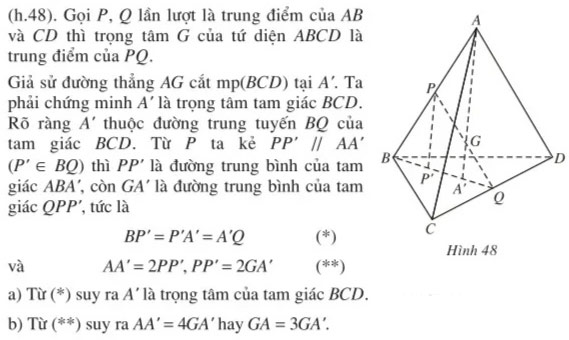
Qua bài tập trên ta có thêm một cách để xác định trọng tâm của tứ diện.
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng:
Trả lời
Theo quy tắc 3 điểm ta có :
Mà G là trọng tâm của tam giác ABC nên:
Từ (1) và (2) ta có:
Bài 2: Cho tứ diện ABCD có P, Q lần lượt là trọng tâm của tam giác ABC và BCD. Giao tuyến của mặt phẳng (ABQ) và mặt phẳng (DCP) là đường thẳng d. Khẳng định nào dưới đây đúng?
A. d đi qua trung điểm hai cạnh AB và CD.
B. d đi qua trung điểm hai cạnh AB và AD.
C. d là đường thẳng PQ.
D. d là đường thẳng QA.
Lời giải:
Đáp án đúng là: A
Gọi M, N lần lượt là trung điểm của AB, CD.
Ta có M ∈ AB mà AB ⊂ (ABQ), nên M ∈ (ABQ) (1)
Khi đó đường trung tuyến CM đi qua trọng tâm P của của ∆ABC.
Do đó mặt phẳng (DCP) chính là mặt phẳng (DCM), nên M ∈ (DCP) (2)
Từ (1) và (2) suy ra M ∈ (ABQ) ∩ (DCP).
Tương tự ta cũng có N ∈ (ABQ) ∩ (DCP).
Suy ra (ABQ) ∩ (DCP) = MN.
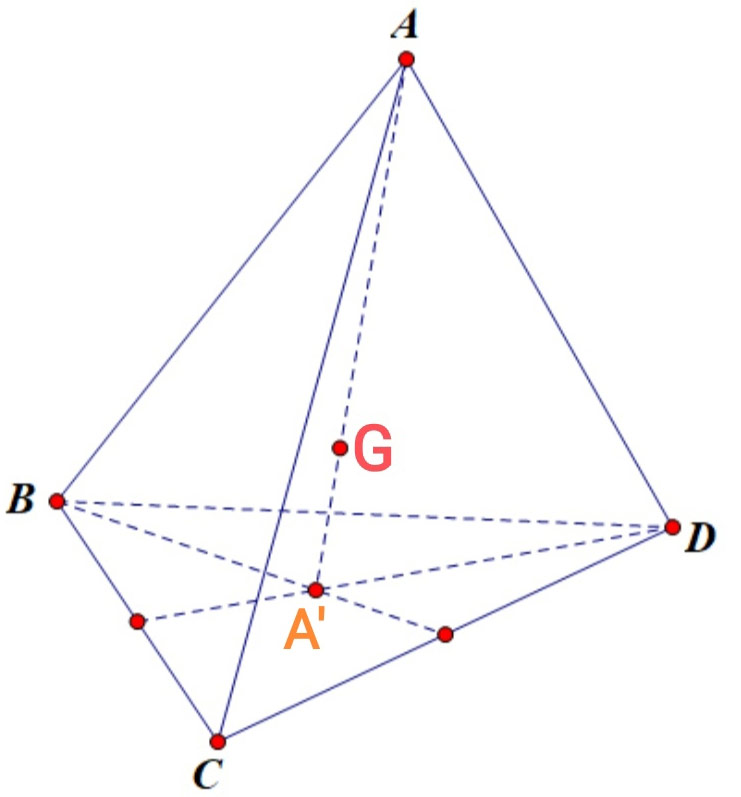
Bài 2: Gọi G là trọng tâm của tứ diện ABCD. A’ là trọng tâm của tam giác BCD. Tính tỉ số GA/GA’ là:
A. 1/2
B. 2
C. 3
D. 1/3
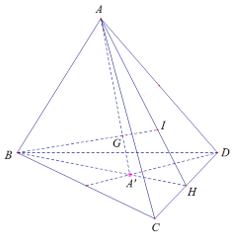
Gọi I là trọng tâm tam giác ACD
H là trung điểm CD
Nối BI cắt AA’, ta được trọng tâm G của tứ diện
Xét mặt phẳng (ABH)
Ta có:
( A’ và I lần lượt là trọng tâm các tam giác BCD và ACD)
A’I // AB
Ta lại có: ( áp dụng định lý ta lét)
GA = 3GA’
Đáp án: D
Giải thích:
Hướng dẫn giải:
Vì I là trọng tâm tam giác ABC nên
→SA+→SB+→SC=3→SI
⇔→SI=13→SA+13→SB+13→SC
Bài 5: Trong không gian Oxyz, cho bốn điểm A(1,0,0);B(0,1,0);C(0,0,1);D(1,1,1). Xác định tọa độ trọng tâm G của tứ diện ABCD.
- A. G(12,12,12)
- B. G(13,13,13)
- C. G(23,23,23)
- D. G(14,14,14)
-
Đáp án đúng: A
- Xem thêm các dạng bài tập hay, có đáp án:
50 Bài tập về chu vi và diện tích của một số hình tứ giác đã học (có đáp án năm 2024) - Toán 6
Cách xác định mặt cầu ngoại tiếp của tứ diện mới nhất 2024
Cách tính bán kính mặt cầu ngoại tiếp tứ diện 2024
50 Bài tập Một số hệ thức về cạnh và góc trong tam giác vuông (có đáp án năm 2024) - Toán 9
50 Bài tập Một số hệ thức về cạnh và đường cao trong tam giác vuông (có đáp án năm 2024) - Toán 9
-