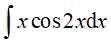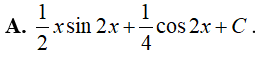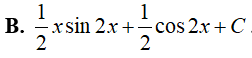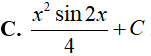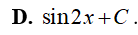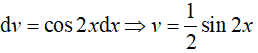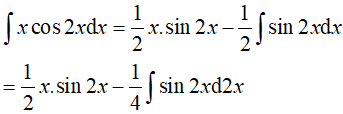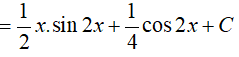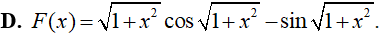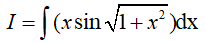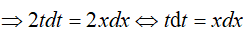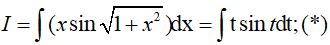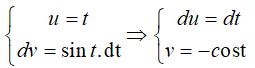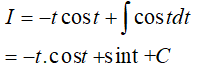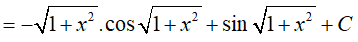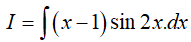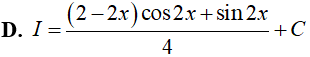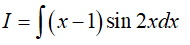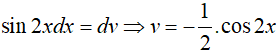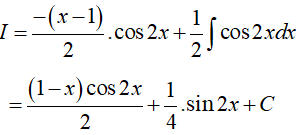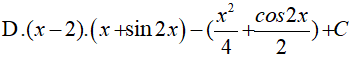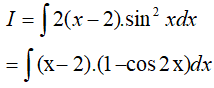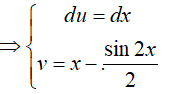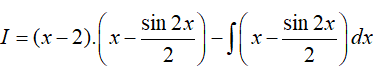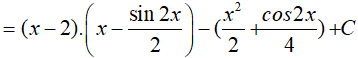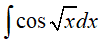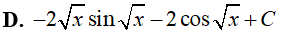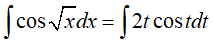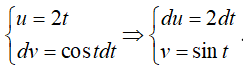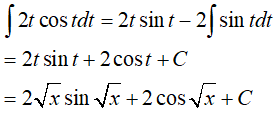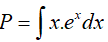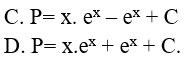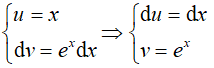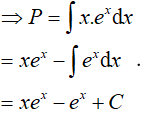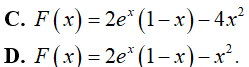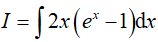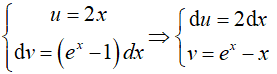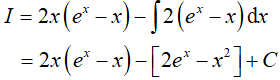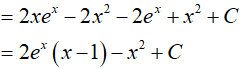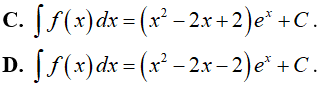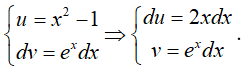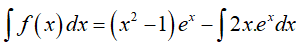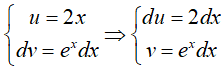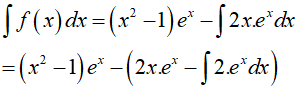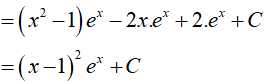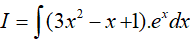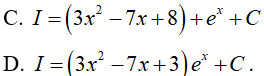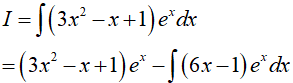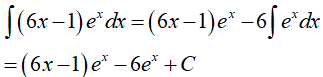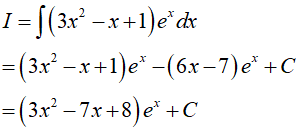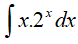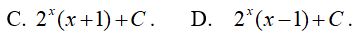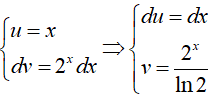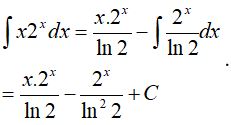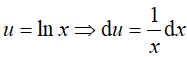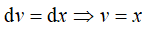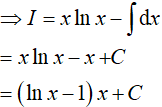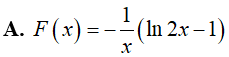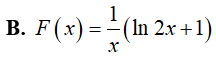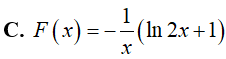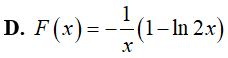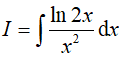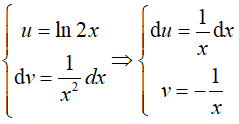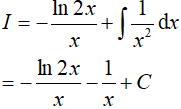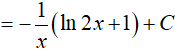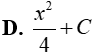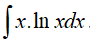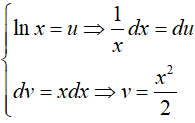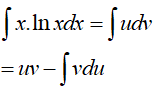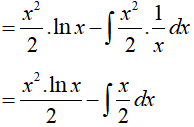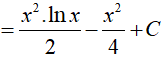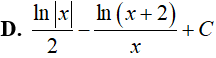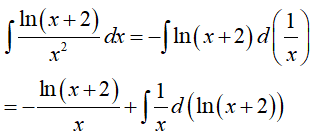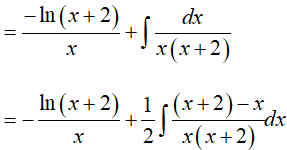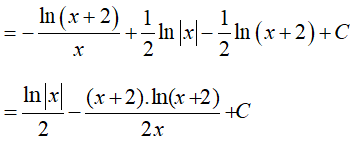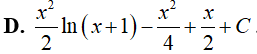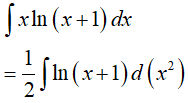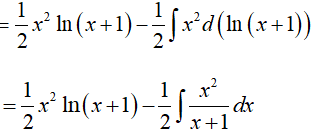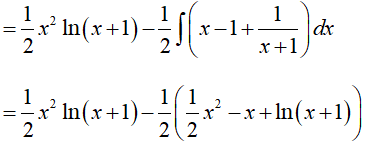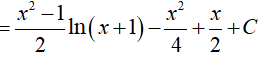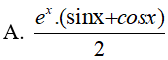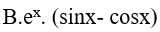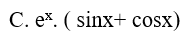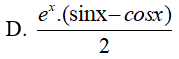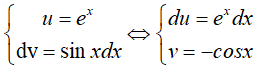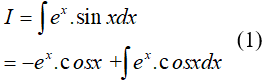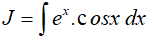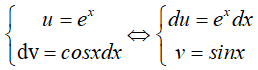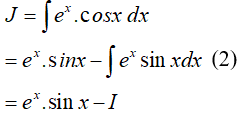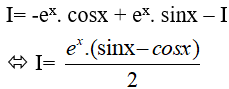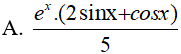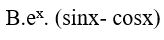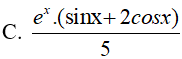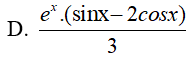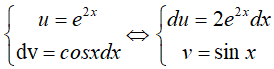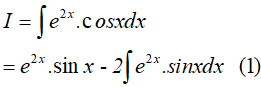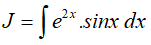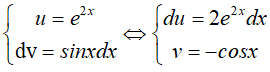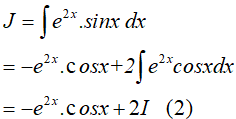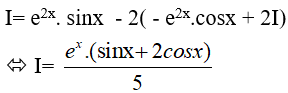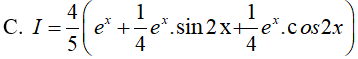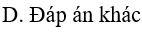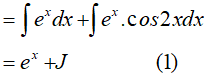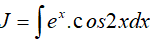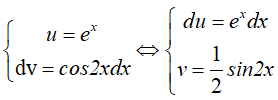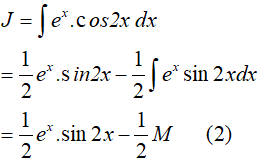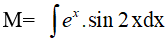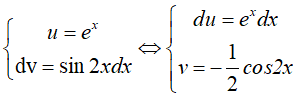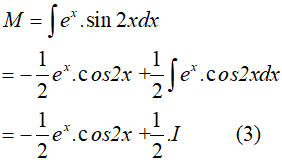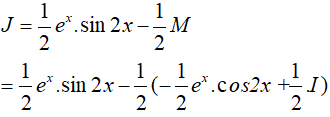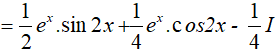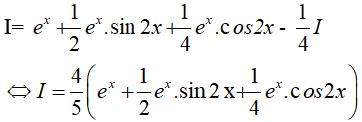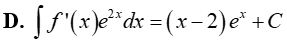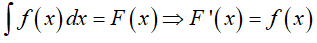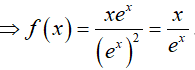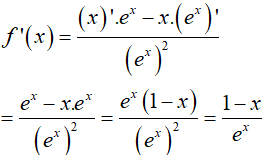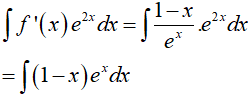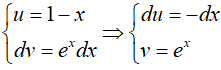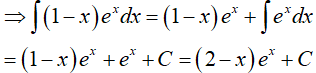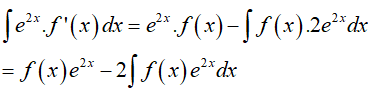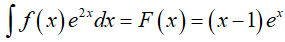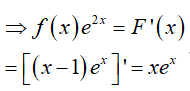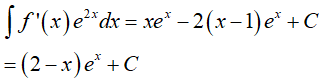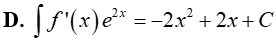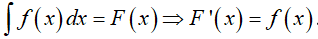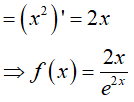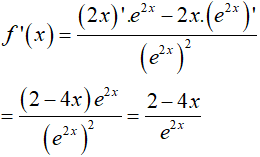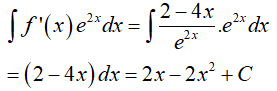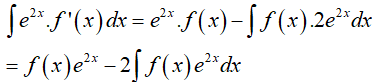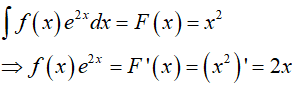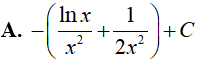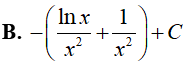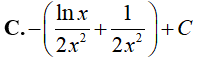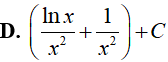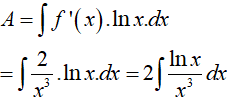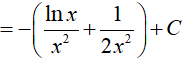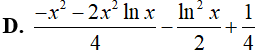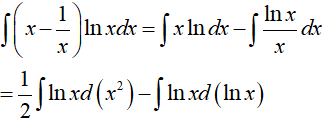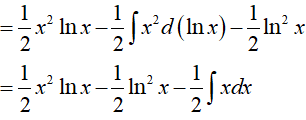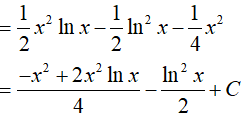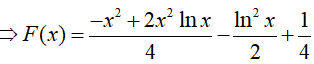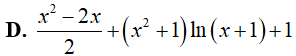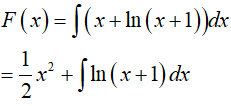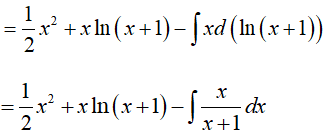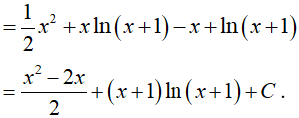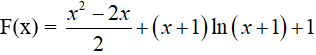Lý thuyết Nguyên hàm từng phần và các dạng bài tập (có đáp án) chi tiết nhất 2024

Công thức nguyên hàm từng phần đầy đủ, chi tiết nhất - Toán lớp 12

1. Lý thuyết

Định lí: Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì:

$$\begin{gathered} \int u\left(x\right)v\text{'}\left(x\right)d\text{x} \\ =u\left(x\right)v\left(x\right)-\int u\text{'}\left(x\right)v\left(x\right)d\text{x} \end{gathered}$$

Hay $\int u\text{d}v=uv-\int v\text{d}u$

Phương pháp:

Cách 1: Sử dụng định lý trên

Bước 1. Chọn u, v sao cho f(x)dx = udv (chú ý dv = v'(x)dx).

Sau đó tính $v=\int \text{d}v$ và du = u'.dx.

Bước 2. Thay vào công thức và tính $v=\int v\text{du}$

Chú ý. Cần phải lựa chọn u và dv hợp lí sao cho ta dễ dàng tìm được v và tích phân $\int v\text{d}u$ dễ tính hơn $\int u\text{d}v$. Ta thường gặp các dạng sau

Dạng 1. $I=\int P\left(x\right)\left[\begin{array}{l}\sin x\\ \cos x\end{array}\right]\text{d}x$, trong đó P(x) là đa thức. Ta đặt $\left\{\begin{array}{l}u=P\left(x\right)\\ \text{d}v=\left[\begin{array}{l}\sin x\\ \cos x\end{array}\right]\text{d}x\end{array}\right.$.

Dạng 2. $I=\int P\left(x\right)e^{ax+b}\text{d}x$, trong đó P(x) là đa thức. Ta đặt $\left\{\begin{array}{l}u=P\left(x\right)\\ \text{d}v=e^{ax+b}\text{d}x\end{array}\right.$.

Dạng 3. $I=\int P\left(x\right)\ln \left(mx+n\right)\text{d}x$, trong đó P(x) là đa thức. Ta đặt $\left\{\begin{array}{l}u=\ln \left(mx+n\right)\\ \text{d}v=P\left(x\right)\text{d}x\end{array}\right.$.

Dạng 4. $I=\int \left[\begin{array}{l}\sin x\\ \cos x\end{array}\right]e^x\text{d}x$. Ta đặt $\left\{\begin{array}{l}u=\left[\begin{array}{l}\sin x\\ \cos x\end{array}\right]\\ \text{d}v=e^x\text{d}x\end{array}\right.$.

Thứ tự ưu tiên đặt u: “Nhất log, nhì đa, tam lượng, tứ mũ” và dv phần còn lại. Nghĩa là nếu có ln hay log_ax thì chọn u=lnx hay $u={\log }_{a}x=\frac{1}{\ln a}.\ln x$ và dv = còn lại. Nếu không có ln; log thì chọn u = đa thức và dv = còn lại. Nếu không có log, đa thức, ta chọn u = lượng giác,….

Cách 2: Sử dụng bảng

Loại 1: Ví dụ: $\int x^3{e}^{x}dx$

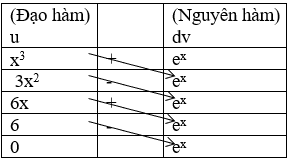
Vậy :

$\int x^3{e}^{x}dx=x^3{e}^x-3x^2{e}^x+6x{e}^x-6e^x+C$

Loại 2: Nguyên hàm lặp. Ví dụ: $\int \cos x{e}^{x}dx$

Vậy

$$\begin{gathered} \int \cos x{e}^{x}dx \\ =\cos x{e}^x-\left(-\sin x\right)e^x+\int -\cos x{e}^{x}dx \\ \Rightarrow \int \cos x{e}^{x}dx=\frac{1}{2}\left(\cos x+\sin x\right)e^x \end{gathered}$$

2. Ví dụ minh họa 

Ví dụ 1: Tính các nguyên hàm

a) $I=\int x{e}^x\text{d}x$

b) $I=\int x\ln xdx$

Lời giải

a) $I=\int x{e}^x\text{d}x$

Đặt $\left\{\begin{array}{l}u=x\\ dv=e^{x}dx\end{array}\right.\Rightarrow \left\{\begin{array}{l}du=dx\\ v=e^x\end{array}\right.$

Theo công thức tính nguyên hàm từng phần, ta có

$$\begin{gathered} I=\int x{e}^{x}dx=x{e}^x-\int e^{x}dx \\ =x{e}^x-e^x+C \end{gathered}$$

b) $I=\int x\ln xdx$

Đặt $\left\{\begin{array}{l}u=\ln x\\ dv=xdx\end{array}\right.\Rightarrow \left\{\begin{array}{l}du=\frac{dx}{x}\\ v=\frac{x^2}{2}\end{array}\right.$

Theo công thức tính nguyên hàm từng phần, ta có:

$$\begin{gathered} I=\int x\ln xdx=\frac{1}{2}{x}^2\ln x-\frac{1}{2}\int xdx \\ =\frac{1}{2}{x}^2\ln x-\frac{1}{4}{x}^2+C \end{gathered}$$

Ví dụ 2: Tính các nguyên hàm sau:

a) $I=\int x^2\cos xdx$

b) $I=\int \sin x.e^x\text{d}x$

Lời giải

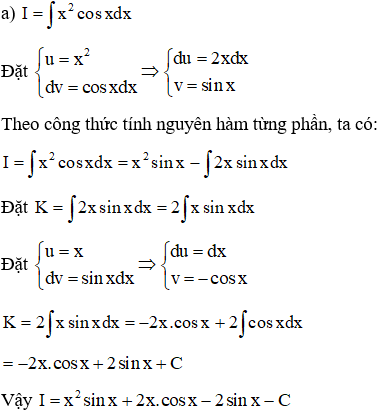
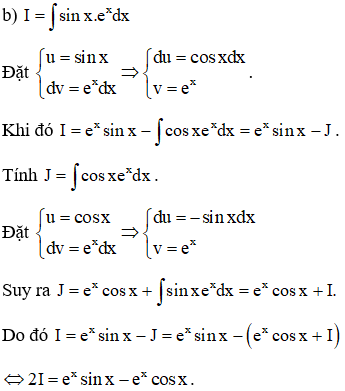
Ví dụ 3. Tìm 

Lời giải

Đáp án: A

Đặt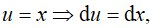  

Ví dụ 4. Một nguyên hàm của hàm số: f(x) = xsin√(1 + x²) là:

   

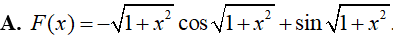
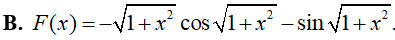
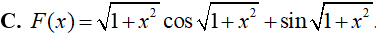
Lời giải

Đáp án: A

* Xét: 

Dùng phương pháp đổi biến: đặt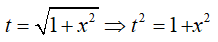  

ta được 

* Dùng phương pháp nguyên hàm từng phần để tính (*):

Đặt 

Ta được

Ví dụ 5. Tìm nguyên hàm 

   

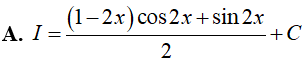
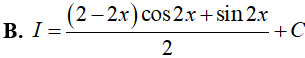
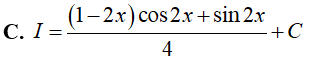
Lời giải

Đáp án: D

Đặt x − 1 = u => dx = du.

Khi đó

Ví dụ 6. Tìm nguyên hàm của hàm số: y = 2(x − 2) .sin²x

   

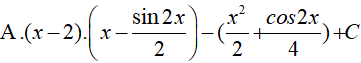
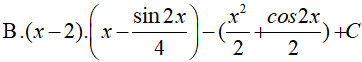
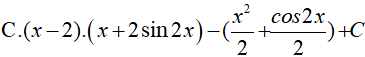
Lời giải

Đáp án: A

Ta có: 2(x − 2).sin²x = (x − 2).(1 − cos2x) vì (cos2x= 1 − 2sin²x)

Do đó,

Đặt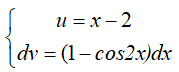  

Suy ra,

Ví dụ 7. Tính 

   

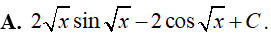
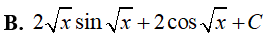
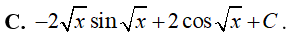
Lời giải

Đáp án: D

Đặt t = √x => t² = x => 2tdt = dx. Ta được 

Đặt 

Do đó,

3. Bài tập vận dụng (có đáp án)

Câu 1. Tính 

 

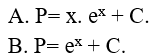
Lời giải

Đáp án: C

Dùng phương pháp từng phần:

Đặt:

Câu 2. Một nguyên hàm của hàm số y = 2x.(e^x − 1) là:

 

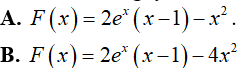
Lời giải

Đáp án: A

Ta có:

Đặt 

Câu 3. Tìm nguyên hàm của hàm số f(x) = (x² − 1)e^x

 

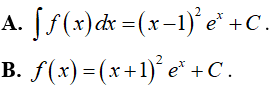
Lời giải

Đáp án: A

Đặt

Suy ra

Đặt

Suy ra

Câu 4. Tìm

 

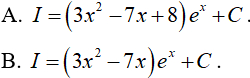
Lời giải

Đáp án: A

Sử dụng phương pháp tính nguyên hàm từng phần, ta có:

Đặt u = 3x² − x + 1 và dv = e^xdx

=> du = (6x − 1)dx và v = e^x. Do đó:

Đặt u₁ = 6x − 1 và dv₁ = e^xdx ta có du₁ = 6dx và v₁ = e^x. Do đó:

Từ đó suy ra:

Câu 5. Tìm

 

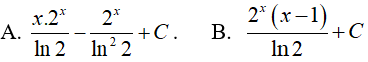
Lời giải

Đáp án: A

Đặt

Ta có:

Câu 6. Chọn câu khẳng định sai?

 

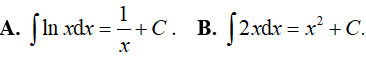
Lời giải

Đáp án: A

* Xét phương án A:

Đặt 

Do đó phương án A sai .

Câu 7. Một nguyên hàm của hàm số 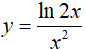 là:

Lời giải

Đáp án: C

Ta có: 

Đặt 

Câu 8. Nguyên hàm của hàm số y= x.lnx là

   

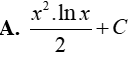
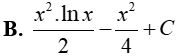
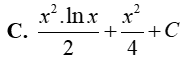
Lời giải

Đáp án: B

Ta có: 

Đặt 

Theo phương pháp nguyên hàm từng phần ta có

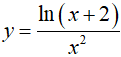
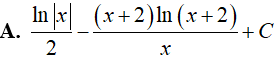
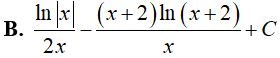
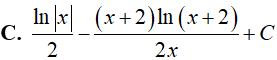
Câu 9. Nguyên hàm của hàm số  là

   

Lời giải

Đáp án: C

Ta có:

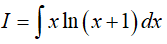
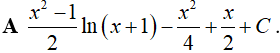
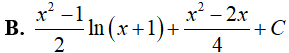
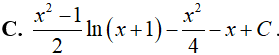
Câu 10. Nguyên hàm  là

   

Lời giải

Đáp án: A

Ta có:

Câu 11. Tìm 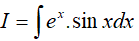 là

Lời giải

Đáp án: A

Đặt 

Ta có: 

* Ta tính 

Đặt 

Suy ra,

Thay (2) vào (1) ta được:

Câu 12. Tìm 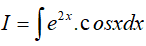 là

Lời giải

Đáp án: C

Đặt 

Ta có: 

* Ta tính 

Đặt 

Suy ra,

Thay (2) vào (1) ta được:

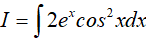
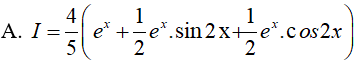
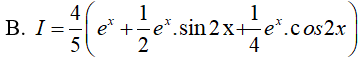
Câu 13. Tính  là

  

Lời giải

Đáp án: B

Ta có: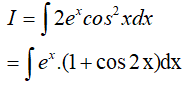  

* Ta tìm 

Đặt 

Suy ra,

Trong đó, 

Đặt 

Ta có: 

Thay (3) vào (2) ta được:

Thay vào (1) ta được:

Câu 14. Cho F(x) = (x − 1).e^x là một nguyên hàm của hàm số f(x). e^2x. Tìm nguyên hàm của hàm số f’(x). e^2x.

   

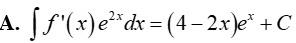
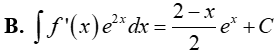
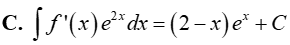
Lời giải

Đáp án: C

Cách 1: Sử dụng tính chất của nguyên hàm 

Từ giả thiết, ta có:

 

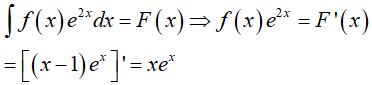
Suy ra

Vậy

Đặt 

Cách 2: Sử dụng công thức nguyên hàm từng phần.

Ta có:

Từ giả thiết: 

Vậy

Câu 15. Cho F(x)= x² là một nguyên hàm của hàm số f(x).e^2x. Tìm nguyên hàm của hàm số f’(x). e^2x?

   

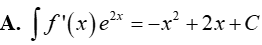
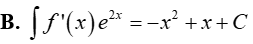
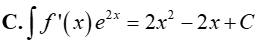
Lời giải

Đáp án: D

Cách 1: Sử dụng tính chất của nguyên hàm 

Từ giả thiết, ta có

 

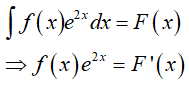
Suy ra

Vậy

Cách 2: Sử dụng công thức nguyên hàm từng phần.

Ta có

Từ giả thiết:

Vậy 

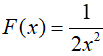
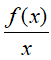
Câu 16. Cho  là một nguyên hàm của hàm số . Tìm nguyên hàm của hàm số f’(x). lnx

Lời giải

Đáp án: A

Từ giả thiết

 

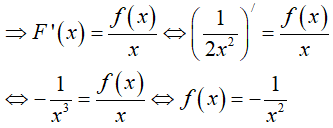
Đặt

Đặt

  

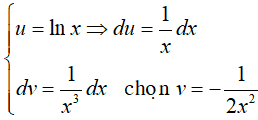
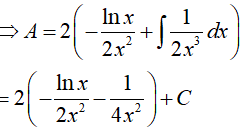
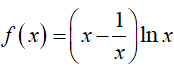
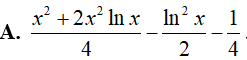
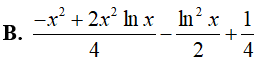
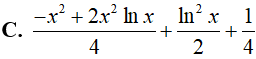
Câu 17. Giả sử F(x) là một nguyên hàm của hàm số  . Biết F(1) = 0. Vậy F(x) bằng:

   

Lời giải

Đáp án: B

Ta có

Mà F(1)= 0 nên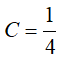  

Câu 18. Gọi F(x) là một nguyên hàm của hàm số f(x) = x + ln(x + 1) . Biết F(0) = 1, vậy F(x) bằng:

   

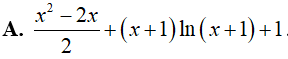
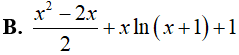
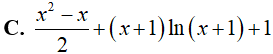
Lời giải

Đáp án: A

Ta có

Lại có F(0) = 1 => C = 1

Vậy

4. Bài tập tự luyện 

Câu 1. Nguyên hàm $I=\frac{1}{5}\int x\cdot {\ln }^{2}xd(5x)=F(x)+C$. Giá trị của F(e) bằng :

A. $\frac{e^2}{2}$

B. $-\frac{e^2}{4}$

C. $\frac{e^2}{4}$

D. $-\frac{e^2}{2}$

Câu 2. Nguyên hàm $I=\int x\cdot \sin x{\cos }^{2}xdx=F(x)+C$. Giá trị của $F(\pi )$ bằng :

A. $-\frac{\pi }{3}$

B. $\frac{\pi }{3}$

C. $\pi$

D. $-\pi$

Câu 3. Nguyên hàm $I=\int e^x\cdot \cos (2x)dx=F(x)+C$. Giá trị của F(0) bằng :

A. $-\frac{1}{5}$

B. $\frac{2}{5}$

C. $-\frac{2}{5}$

D. $\frac{1}{5}$

Câu 4. Nguyên hàm $\int (x-2)\sin 3xdx=-\frac{(x-a)\cos 3x}{b}+\frac{\sin 3x}{c}+2017$ thì tổng S=a b+c bằng

A. S=14.

B. S=15.

C. S=3.

D.S=10

Câu 5. Nguyên hàm $\int x^2\cdot e^{x}dx=\left(x^2+mx+n\right)\cdot e^x+C$thì giá trị mn là:

A. 6

B. 4

C. 0

D. -4

Câu 6. Biết $I={\int }_0^{1}x\cdot \ln \left(\frac{4-x}{4+x}\right)dx=-\frac{15}{2}\ln \frac{a}{b}-c$, với $a,b,c\in \mathbb{N}$ và phân số $\frac{a}{b}$ tối giản

Tìm khẳng định đúng :

A. a+b=2c.

B. b+b=3c.

C. a+b=c

D. a+b=4 c

Câu 7. Biết $I={\int }_1^2\left(x^2+x\right)\cdot \ln xdx=\frac{a}{3}\ln 2-\frac{b}{c}$, với $a,b,c\in \mathbb{N}$ và phân số $\frac{b}{c}$ tối giản

Tính tổng S=a b+c bằng :

A. 806

B. 559

C. 1445

D. 1994

Câu 8. Biết $I={\int }_0^{\frac{\pi }{2}}{e}^{2x}\cdot \sin (3x)dx=\frac{a-b\cdot e^{\pi }}{c}$, chọn khẳng định đúng :

A. a, b, c là số nguyên tố

B. a, c là số nguyên tố

C. b, c là số nguyên tố

D. a, b là số nguyên tố

Câu 9. Hàm số $f(x)=\left(a{x}^2+bx+c\right)e^{-x}$ là một nguyên hàm của $g(x)=x(1-x)e^{-x}$.

Tính tổng a+b+c :

A. 4

B. $-2$

C. 3

D. 1

Câu 10. Nguyên hàm $I=-\int \left(x^2-3x+2\right)\left(4{\cos }^{3}x-3\cos x\right)d(\cos x)=F(x)+C$.

Giá trị của F(0) bằng:

A. $-\frac{3}{64}$

B. $\frac{9}{64}$

C. $\frac{9}{32}$

D. Đáp án khác

Xem thêm các dạng bài tập liên quan khác:

60 Bài tập về Nguyên hàm ( có đáp án năm 2023 )

60 Bài tập về Tích phân (có đáp án năm 2024)

60 Bài tập về ứng dụng hình học của tích phân (có đáp án năm 2023)

60 Bài tập về số phức (có đáp án năm 2023)

60 Bài tập về phép chia số phức (có đáp án năm 2023)