Trắc nghiệm Toán 7 Ôn tập chương 4 có đáp án
-
297 lượt thi
-
30 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Góc ngoài của tam giác là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Góc ngoài của tam giác là góc kề bù với một góc trong của tam giác và bằng tổng hai góc trong không kề với nó.
Câu 2:
Trường hợp bằng nhau cạnh – cạnh – cạnh của hai tam giác là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Trường hợp bằng nhau cạnh – cạnh – cạnh của hai tam giác là:
Nếu 3 cạnh của tam giác này bằng 3 cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Câu 3:
Tổng ba góc ngoài (mỗi đỉnh của tam giác ta chỉ lấy một góc) của một tam giác bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Góc ngoài bằng tổng hai góc trong không kề với nó.
Do đó tổng 3 góc ngoài tam giác bằng 2 lần tổng 3 góc trong tam giác.
Mà tổng 3 góc trong tam giác là 180°
Nên tổng ba góc ngoài của một tam giác bằng 360°.
Câu 4:
Cho \(\Delta ABC\) (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) bằng một tam giác có ba đỉnh là H, I, K. Viết kí hiệu về sự bằng nhau của hai tam giác, biết rằng AB = IK, BC = KH.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có:
AB = IK ⇒ đỉnh tương ứng của B là I hoặc K. (1)
BC = KH ⇒ đỉnh tương ứng của B là K hoặc H. (2)
Từ (1) và (2) ⇒ đỉnh tương ứng của B là K.
Do đó đỉnh tương ứng của A là I, đỉnh tương ứng của C là H.
⇒ \[\Delta ABC = \Delta IKH\].
Câu 5:
Cho \[\Delta ABC = \Delta MNP\]. Trong các khẳng định sau đây khẳng định nào sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì \[\Delta ABC = \Delta MNP\] nên
\(\widehat B = \widehat N\); \(\widehat P = \widehat C\) (các góc tương ứng bằng nhau).
BC = NP (2 cạnh tương ứng bằng nhau)
Vậy BC = MP là khẳng định sai.
Câu 6:
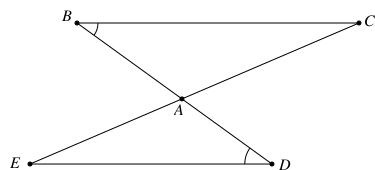
Cho hình dưới đây, số đo góc DCx là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét tam giác ABC có AB = AC ⇒ Tam giác ABC cân tại A ⇒ \(\widehat {ABC} = \widehat {ACB}\) (tính chất tam giác cân)
Mà: \(\widehat {ABC} + \widehat {ACB} + \widehat A = 180^\circ \) (tổng 3 góc trong tam giác)
⇒ \(\widehat {ABC} = \widehat {ACB} = \frac{{180^\circ - \widehat A}}{2} = \frac{{180^\circ - 90^\circ }}{2} = 45^\circ \)
Góc BCx là góc ngoài của tam giác ABC tại đỉnh C
⇒ \(\widehat {BCx} = \widehat {ABC} + \widehat A = 45^\circ + 90^\circ = 135^\circ \)
Xét tam giác DBC có BC = BD = DC ⇒ tam giác DBC là tam giác đều
⇒ \(\widehat {BCD} = 60^\circ \) (tính chất tam giác đều)
Có: \(\widehat {BCD} + \widehat {DCx} = \widehat {BDx}\)
⇒ \(60^\circ + \widehat {DCx} = 135^\circ \)
⇒ \(\widehat {DCx} = 75^\circ \)
Câu 7:
Cho tam giác ABC bằng tam giác DEF, góc tương ứng với góc C là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Tam giác ABC bằng tam giác DEF nên
Góc A tương ứng với góc D
Góc B tương ứng với góc E
Góc C tương ứng với góc F
Câu 8:
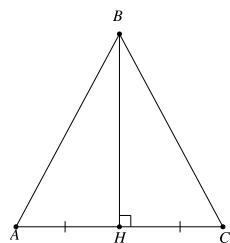
Cho hình vẽ. Với các kí hiệu trên hình vẽ, cần thêm yếu tố nào để \(\Delta ABC = \Delta ADE\) (g.c.g)
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xét tam giác ABC và tam giác ADE có:
\(\widehat B = \widehat D\)
\(\widehat {BAC} = \widehat {DAE}\) (2 góc đối đỉnh)
Mà \(\widehat B\) và \(\widehat {BAC}\) là hai góc kề của cạnh AB; \(\widehat D\) và \(\widehat {DAE}\) là hai góc kề của cạnh AD
Vậy để 2 tam giác bằng nhau theo trường hợp g.c.g cần có thêm điều kiện AB = AD.
Câu 9:
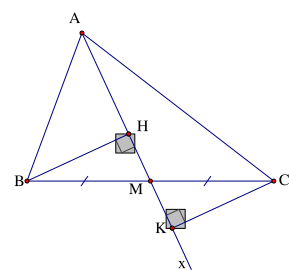
Hình vẽ dưới đây có tam giác bằng nhau là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Xét tam giác ABH vuông tại H và tam giác CBH vuông tại H có:
AH = CH
BH là cạnh chung
Nên \(\Delta ABH = \Delta CBH\) (2 cạnh góc vuông)
(đỉnh A tương ứng với đỉnh X; đỉnh B của tam giác này tương ứng với đỉnh B của tam giác kia; đỉnh H của tam giác này tương ứng với đỉnh H của tam giác kia).
Câu 10:
Cho hình sau, cần bổ sung thêm điều kiện gì để tam giác ACP bằng tam giác ABN theo trường hợp cạnh- góc- cạnh

 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xét tam giác ACP và tam giác ABN có
\(\widehat {APC} = \widehat {ANB}\)
Mà góc APC là góc xen giữa hai cạnh AP và CP; góc ANB là góc xen giữa hai cạnh AN và BN.
Tam giác ACP và tam giác ABN thì cạnh AN = AP và CP = BN (các cạnh tương ứng)
Vậy cần thêm điều kiện AN = AP và CP = BN thì tam giác ACP bằng tam giác ABN theo trường hợp cạnh- góc- cạnh.
Câu 11:
Cho \[\Delta ABC = \Delta MNP\] trong đó \(\widehat A = 30^\circ \), \(\widehat P = 60^\circ \). So sánh các góc N, M, P.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì \[\Delta ABC = \Delta MNP\] nên \(\widehat M = \widehat A = 30^\circ \) (hai góc tương ứng bằng nhau)
Xét \(\Delta MNP\) ta có \(\widehat M + \widehat N + \widehat P = 180^\circ \) (tổng ba góc của một tam giác)
⇒ \(\widehat N = 180^\circ - \left( {\widehat M + \widehat P} \right)\)
⇒ \(\widehat N = 180^\circ - \left( {30^\circ + 60^\circ } \right) = 90^\circ \)
Do \(90^\circ > 60^\circ > 30^\circ \,\,{\rm{hay}}\,\,\widehat N > \widehat P > \widehat M\).
Câu 12:
Cho \(\Delta DEF = \Delta MNP\). Biết EF + FD = 10 cm, NP – MP = 2 cm. Tính độ dài cạnh FD.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vì \(\Delta DEF = \Delta MNP\) nên MN = DE, EF = NP, DF = MP (các cạnh tương ứng bằng nhau).
Theo bài ra ta có NP – MP = 2 cm ⇒ EF – DF = 2 cm (1)
Lại có EF + DF = 10 cm (2)
Từ (1) và (2) \(DF = \frac{{10 - 2}}{2} = 4\,\left( {{\mathop{\rm cm}\nolimits} } \right)\)
Vậy DF = 4 cm.
Câu 13:
Cho tam giác ABC có M là trung điểm cạnh BC. Kẻ tia Ax đi qua M. Qua B, C lần lượt kẻ các đường thẳng vuông góc với Ax, cắt Ax tại H, K. So sánh BH và CK.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xét \[\Delta BHM\] và \[\Delta CKM\] có:
\[\widehat {BHM} = \widehat {CKM}\,( = {90^{\rm{o}}})\]
BM = CM (Vì M là trung điểm cạnh BC)
\[\widehat {BMH} = \widehat {CMK}\] (hai góc đối đỉnh)
⇒ \[\Delta BHM = \Delta CKM\] (cạnh huyền – góc nhọn)
Suy ra BH = CK (hai cạnh tương ứng)
Câu 14:
Cho tam giác ABC vuông tại A, BD là tia phân giác của góc ABC và BA = BE (E thuộc BC). Số đo góc BED là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét tam giác ABD và tam giác EBD có:
BA = BE (theo giả thiết)
\(\widehat {ABD} = \widehat {EBD}\) (BD là tia phân giác của \(\widehat {ABC}\))
BD là cạnh chung
⇒ \(\Delta ABD = \Delta EBD\) (c.g.c)
⇒ \(\widehat {BAD} = \widehat {BED}\) (hai góc tương ứng)
Mà \(\widehat {BAD} = 90^\circ \)(theo giả thiết) ⇒ \(\widehat {BED} = 90^\circ \)
Câu 15:
Cho M, N là hai điểm phân biệt nằm trên đường trung trực của cạnh AB sao cho AM = BN. O là giao điểm của MN và AB. Khẳng định sai là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
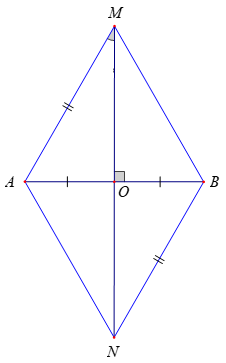
MN là đường trung trực của AB
⇒ MN ⊥ AB tại O và OA = OB
+) Xét hai tam giác vuông AMO và BNO có:
AM = BN (theo giả thiết)
OA = OB
⇒ \(\Delta AMO = \Delta BNO\) (cạnh huyền – cạnh góc vuông)
+) Ta có: AN = BN (vì N thuộc đường trung trực của AB) ⇒ \(\Delta ANB\) cân tại N.
Mà AM = BN (theo giả thiết)
⇒ AN = AM
⇒ \(\Delta AMN\) cân tại A (đpcm)
+) Có: MA = MB (vì M thuộc đường trung trực của AB)
⇒ \(\Delta AMB\) là tam giác cân tại M.
Câu 16:
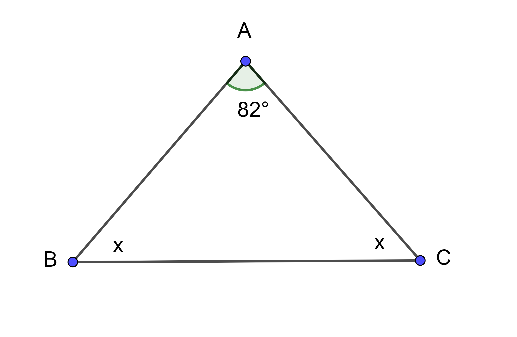
Cho hình vẽ sau, số đo x là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Xét tam giác ABC có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng 3 góc trong tam giác)
⇒ \(82^\circ + x + x = 180^\circ \)
⇒ \(2x = 180^\circ - 82^\circ \)
⇒ \(2x = 98^\circ \)
⇒ \(x = 49^\circ \)
Câu 17:
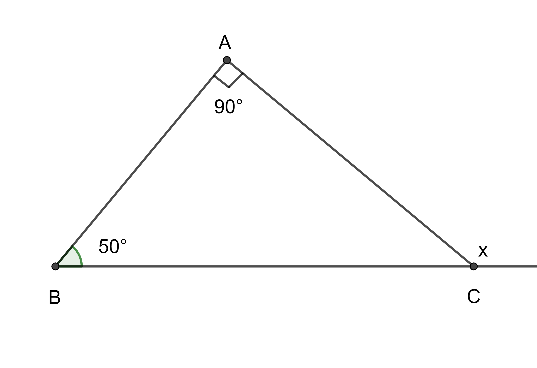
Cho hình vẽ sau. Số đo x bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: \(x = \widehat A + \widehat B\) (góc ngoài của tam giác)
⇒ \(x = 90^\circ + 50^\circ \)
⇒ \(x = 140^\circ \)
Câu 18:
Cho hình vẽ dưới đây, biết JG = JL, GK = LK, \(\widehat {KJL} = 60^\circ \), \(\widehat {JGK} = 90^\circ \).
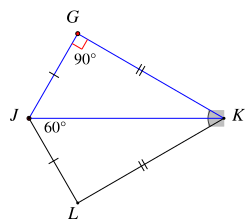
Số đo góc GKL là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét hai tam giác JGK và JLK có:
JG = JL (theo giả thiết)
GK = LK (theo giả thiết)
JK là cạnh chung
Vậy \(\Delta JGK = \Delta JLK\) (c.c.c)
⇒ \(\widehat {KJG} = \widehat {KJL}\)(hai góc tương ứng)
⇒ \(\widehat {KJG} = 60^\circ \)
Xét tam giác JGK có: \(\widehat {KJG} + \widehat {JGK} + \widehat {GKJ} = 180^\circ \) (tổng 3 góc trong tam giác)
⇒ \(60^\circ + 90^\circ + \widehat {GKJ} = 180^\circ \)
⇒ \(\widehat {GKJ} = 180^\circ - 60^\circ - 90^\circ = 30^\circ \)
Vì\(\Delta JGK = \Delta JLK\) (theo câu a)
⇒ \(\widehat {GKJ} = \widehat {LKJ}\)(hai góc tương ứng)
⇒ \(\widehat {GKL} = \widehat {GKJ} + \widehat {LKJ} = \widehat {GKJ} + \widehat {GKJ} = 2\widehat {GKJ} = 2 \cdot 30^\circ = 60^\circ \)
Vậy \(\widehat {GKL} = 60^\circ \).
Câu 19:
Cho \[\Delta DEF\] có \(\widehat E = \widehat F\). Tia phân giác của góc D cắt EF tại I. Ta có
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
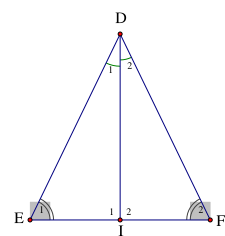
+ Xét \[\Delta DEI\] có:
\[\widehat {{D_1}} + \widehat {{E_1}} + \widehat {{I_1}} = {180^{\rm{o}}}\] (ĐL tổng ba góc của tam giác)
+ Xét \[\Delta DFI\] có:
\[\widehat {{D_2}} + \widehat {{F_2}} + \widehat {{I_2}} = {180^{\rm{o}}}\] (ĐL tổng ba góc của tam giác)
Mà: \(\widehat {{E_1}} = \widehat {{F_2}}\) (gt) và \(\widehat {{D_1}} = \widehat {{D_2}}\) (Vì DI là tia phân giác của góc \[D\])
Nên: \(\widehat {{I_1}} = \widehat {{I_2}}\) (Hay \[\widehat {DIE} = \widehat {DIF}\]) (A và D sai)
+ Xét \[\Delta DEI\] và \[\Delta DFI\], có:
\(\widehat {{D_1}} = \widehat {{D_2}}\) (cmt)
DI là cạnh chung
\(\widehat {{I_1}} = \widehat {{I_2}}\) (cmt)
\[ \Rightarrow \Delta DIE = \Delta DIF\] (g.c.g) (B sai)
Suy ra IE = IF; DE = DF (2 cạnh tương ứng)
Vậy C đúng.
Câu 20:
Cho hình vẽ sau, trong đó \(AB{\rm{//}}CD\), AB = CD. Khẳng định đúng là
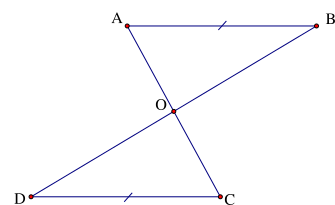
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xét \[\Delta AOB\] và \[\Delta COD\] có:
\(\widehat {OAB} = \widehat {OCD}\) (2 góc so le trong do \(AB{\rm{//}}CD\))
AB = CD (gt)
\(\widehat {OBA} = \widehat {ODC}\) (2 góc so le trong do \(AB{\rm{//}}CD\))
\[ \Rightarrow \Delta AOB = \Delta COD\] (g.c.g)
Suy ra OA = OC (hai cạnh tương ứng)
Câu 21:
Cho hình vẽ dưới đây, biết AE = CE, DE = BE. Khẳng định đúng là
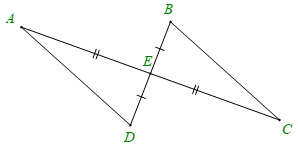
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Hai tam giác AED và CEB có:
AE = CE
\(\widehat {AED} = \widehat {CEB}\) (hai góc đối đỉnh)
DE = BE
Do đó \(\Delta AED = \Delta CEB\) (c.g.c)
Câu 22:
Cho \[\Delta ABC = \Delta MNP\] biết AC = 5 cm. Cạnh nào của \[\Delta MNP\]có độ dài bằng 5 cm?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì \[\Delta ABC = \Delta MNP\] nên
AC = MP (hai cạnh tương ứng bằng nhau)
Mà AC = 5 cm
Nên MP = 5 cm
Câu 23:
Cho \(\Delta ABC\) (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) bằng một tam giác có ba đỉnh là T, S, R. Viết kí hiệu về sự bằng nhau của hai tam giác, biết rằng \(\widehat A = \widehat T\), AC = TS.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có:
\(\widehat A = \widehat T\) ⇒ A, T là hai đỉnh tương ứng.
AC = TS ⇒ C, S là hai đỉnh tương ứng.
Do đó B, R là hai đỉnh tương ứng.
\( \Rightarrow \)\[\Delta ABC = \Delta TRS\].
Câu 24:
Cho tam giác ABC có AB = AC . Trên cạnh AB và AC lấy các điểm D, E sao cho AD = AE. Gọi K là giao điểm của BE và CD. Chọn câu sai.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
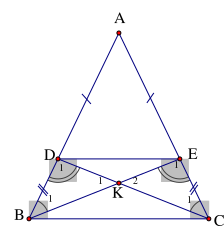
+ Có: AB = AC, AD = AE (gt)
AB = AD + DB, AC = AE + EC
Suy ra: DB = EC (A đúng)
+ Xét \[\Delta ABE\] và \[\Delta ACD\] có:
AB = AC (gt)
\[\widehat {BAC}\] là góc chung
AE = AD (gt)
\[\Delta ABE = \Delta ACD\] (c.g.c)
⇒ BE = CD (2 cạnh tương ứng) (B đúng)
và \(\widehat {{B_1}} = \widehat {{C_1}}\); \(\widehat {AEB} = \widehat {ADC}\) (2 góc tương ứng)
+ Có \[\widehat {ADC} + \widehat {{D_1}} = {180^{\rm{o}}}\] (2 góc kề bù)
\[\widehat {AEB} + \widehat {{E_1}} = {180^{\rm{o}}}\] (2 góc kề bù)
Mà \(\widehat {AEB} = \widehat {ADC}\) (cmt) ⇒ \(\widehat {{D_1}} = \widehat {{E_1}}\)
Xét \[\Delta BDK\] và \[\Delta CEK\] có:
\(\widehat {{B_1}} = \widehat {{C_1}}\) (cmt)
DB = EC (cmt)
\(\widehat {{D_1}} = \widehat {{E_1}}\) (cmt)
\[ \Rightarrow \Delta BDK = \Delta CEK\] (g.c.g)
Suy ra \[BK = KC\] (C đúng; D sai)
Câu 25:
Cho hình vẽ dưới đây. Khẳng định đúng là
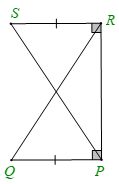
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Hai tam giác SRP (vuông tại R) và tam giác QPR (vuông tại P) có:
RP là cạnh chung
SR = QP
Nên \(\Delta SRP = \Delta QPR\) (hai cạnh góc vuông).
(Đỉnh S tương ứng với đỉnh Q; đỉnh R của tam giác này tương ứng với đỉnh P của tam giác kia và ngược lại).
Câu 26:
Cho tam giác ABC vuông tại A và tam giác POI vuông tại I có BC = OP, \(\widehat C = \widehat P\). Khẳng định đúng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xét tam giác ABC vuông tại A và tam giác IOP vuông tại I có
BC = OP
\(\widehat C = \widehat P\)
Nên \(\Delta ABC = \Delta IOP\) (cạnh huyền – góc nhọn)
⇒ AB = IO (hai cạnh tương ứng)
\(\widehat B = \widehat O\) (hai góc tương ứng)
Vậy khẳng định D đúng.
Câu 27:
Cho hình vẽ dưới đây, biết AB vuông góc với BC, AD vuông góc với CD và cạnh AB = AD. Khẳng định sai là

 Xem đáp án
Xem đáp án
Đáp án đúng là: D
a) Xét tam giác BAC (vuông tại B) và tam giác DAC (vuông tại D) có:
AC là cạnh chung
AB = AD (theo giả thiết)
⇒ \(\Delta BAC = \Delta DAC\) (cạnh huyền – cạnh góc vuông) (A đúng)
b) Vì \(\Delta BAC = \Delta DAC\) (theo câu a) ⇒ \(\widehat {BAC} = \widehat {DAC}\) (hai góc tương ứng) hay \(\widehat {BAH} = \widehat {DAH}\)
Xét tam giác BAH và tam giác DAH có:
AB = AD (theo giả thiết)
\(\widehat {BAH} = \widehat {DAH}\) (chứng minh trên)
AH là cạnh chung
⇒ \(\Delta BAH = \Delta DAH\) (c.g.c) (B đúng)
⇒ \(\widehat {AHB} = \widehat {AHD}\) (hai góc tương ứng)
Mà \(\widehat {AHB} + \widehat {AHD} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {AHB} = \widehat {AHD} = 90^\circ \)
⇒ AC ⊥ BD (đpcm). (C đúng)
Khẳng định D sai.
Câu 28:
Cho tam giác MNP cân tại M có \(\widehat P = 50^\circ \). Số đo góc M là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Tam giác MNP cân tại M nên \(\widehat N = \widehat P\) ⇒ \(\widehat N = \widehat P = 50^\circ \)
Có \(\widehat N + \widehat P + \widehat M = 180^\circ \) (tổng 3 góc trong tam giác)
⇒ \(50^\circ + 50^\circ + \widehat M = 180^\circ \)
⇒ \(\widehat M = 80^\circ \)
Câu 29:
Cho điểm M thuộc đường trung trực của đoạn thẳng AB sao cho góc MAB bằng 60°. Khẳng định đúng nhất là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
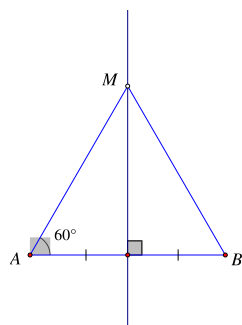
M thuộc đường trung trực của đoạn thẳng AB nên MA = MB (tính chất đường trung trực)
Do đó tam giác MAB cân tại M
Mà \(\widehat {MAB} = 60^\circ \) nên tam giác MAB đều.
Câu 30:
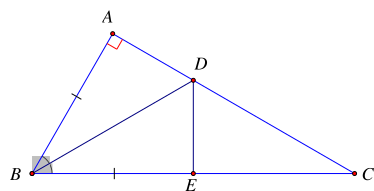
Cho hình vẽ dưới đây. Tam giác ABC cân tại B, D là trung điểm của AC. Biết \(\widehat {AEC} = 110^\circ \), tổng \(\widehat {ABE} + \widehat {BAE}\) là
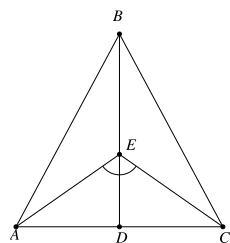
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét tam giác BAD và tam giác BCD có:
BA = BC (\(\Delta ABC\) cân tại B)
AD là cạnh chung
AD = CD (D là trung điểm của AC)
⇒ \(\Delta BAD = \Delta BCD\) (c.c.c)
⇒ \(\widehat {BDA} = \widehat {BDC}\) (hai góc tương ứng)
Mà \(\widehat {BDA} + \widehat {BDC} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {BDA} = \widehat {BDC} = 90^\circ \)
Xét tam giác ADE vuông tại D và tam giác CDE vuông tại D có:
AD = CD
DE là cạnh chung
⇒ \(\Delta ADE = \Delta CDE\) (hai cạnh góc vuông)
⇒ \(\widehat {AED} = \widehat {CED}\) (hai góc tương ứng)
Mà \(\widehat {AEC} = 110^\circ \)
⇒ \(\widehat {AED} = \widehat {CED} = \frac{{\widehat {AEC}}}{2} = 55^\circ \)
Ta có góc AED là góc ngoài tại đỉnh E của tam giác ABE nên
\(\widehat {ABE} + \widehat {BAE} = \widehat {AED} = 55^\circ \)