Trắc nghiệm Toán 7 Bài 16. Tam giác cân. Đường trung trực của đoạn thẳng có đáp án
Trắc nghiệm Toán 7 Bài 16. Tam giác cân. Đường trung trực của đoạn thẳng có đáp án
-
345 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC cân tại A. Khẳng định đúng là
Xem đáp án
Đáp án đúng là: A
Tam giác ABC cân tại A thì AB = AC; \(\widehat B\) = \(\widehat C\).
Câu 2:
Khẳng định nào sau đây sai?
Xem đáp án
Đáp án đúng là: D
Tam giác cân có:
- Hai cạnh bằng nhau;
- Hai góc ở đáy bằng nhau.
Tam giác đều có:
- Ba cạnh bằng nhau.
- Ba góc bằng nhau và bằng 60°
Giải sử tam giác ABC cân tại A ⇒ \(\widehat B\) = \(\widehat C\)
Mà tổng 3 góc trong tam giác là 180°
⇒ \(\widehat B\) = \(\widehat C\) = \(\frac{{180^\circ - \widehat A}}{2}\) < \(90^\circ - \frac{{\widehat A}}{2}\) < 90°
Vậy trong tam giác cân có hai góc ở đáy luôn là góc nhọn, do đó không thể có hai góc tù.
Câu 3:
Đường trung trực của một đoạn thẳng là
Xem đáp án
Đáp án đúng là: C
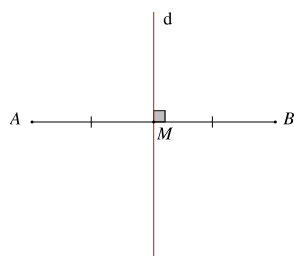
Đường thẳng vuông góc với đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.
Ví dụ: Đường thẳng d vuông góc với đoạn AB tại M và M là trung điểm của AB. Khi đó d được gọi là đường trung trực của đoạn thẳng AB.
Câu 4:
Cho điểm D nằm trên đường trung trực của đoạn thẳng AB. Khẳng định đúng là
Xem đáp án
Đáp án đúng là: B
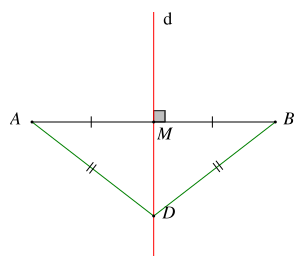
Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Đường thẳng d là đường trung trực của đoạn thẳng AB và D ∈ d.
Khi đó DA = DB.
Câu 5:
Cho tam giác ABC có \(\widehat A = \widehat B\). Khẳng định đúng là
Xem đáp án
Đáp án đúng là: D
Tam giác ABC có \(\widehat A = \widehat B\) nên tam giác ABC là tam giác cân tại C.
Câu 6:
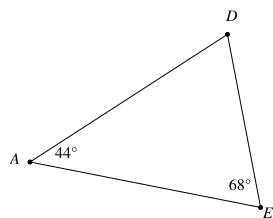
Cần thêm điều kiện gì để tam giác EAD trong hình vẽ dưới đây là tam giác cân:
Xem đáp án
Đáp án đúng là: A
Xét tam giác EDA có: \(\widehat E + \widehat A + \widehat D = 180^\circ \) (tổng 3 góc trong tam giác)
⇒ \(68^\circ + 44^\circ + \widehat D = 180^\circ \)
⇒ \(\widehat D = 68^\circ \)
⇒ \(\widehat D = \widehat E\,\,\left( { = 68^\circ } \right)\)
⇒ Tam giác EDA cân tại A.
Vậy không cần thêm điều kiện gì.
Câu 7:
Cho tam giác MNP cân tại M có MN = 6 cm; NP = 7 cm. Chu vi tam giác MNP là
Xem đáp án
Đáp án đúng là: B
Tam giác MNP cân tại M nên MN = MP ⇒ MP = MN = 6 cm
Chu vi tam giác MNP là: MN + NP + MP = 6 + 7 + 6 = 19 (cm)
Câu 8:
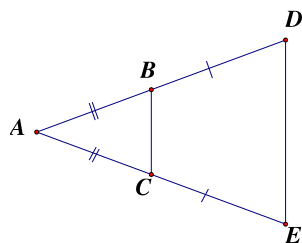
Hình dưới đây có các tam giác cân là
Xem đáp án
Đáp án đúng là: C
Xét tam giác CAB có: AB = AC
⇒ tam giác CAB cân tại A.
Có: AB = AC và BD = CE
Mà: AD = AB + BD; AE = AC + CE
Nên AD = AE
⇒ tam giác EAD cân tại A.
Câu 9:
Cho tam giác MNP cân tại M có \(\widehat P = 50^\circ \). Số đo góc M là
Xem đáp án
Đáp án đúng là: B
Tam giác MNP cân tại M nên \(\widehat N = \widehat P\) ⇒ \(\widehat N = \widehat P = 50^\circ \)
Có \(\widehat N + \widehat P + \widehat M = 180^\circ \) (tổng 3 góc trong tam giác)
⇒ \(50^\circ + 50^\circ + \widehat M = 180^\circ \)
⇒ \(\widehat M = 80^\circ \)
Câu 10:
Cho điểm M thuộc đường trung trực của đoạn thẳng AB sao cho góc MAB bằng 60°. Khẳng định đúng nhất là
Xem đáp án
Đáp án đúng là: B
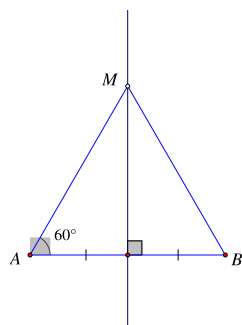
M thuộc đường trung trực của đoạn thẳng AB nên MA = MB (tính chất đường trung trực)
Do đó tam giác MAB cân tại M
Mà \(\widehat {MAB} = 60^\circ \) nên tam giác MAB đều.
Câu 11:
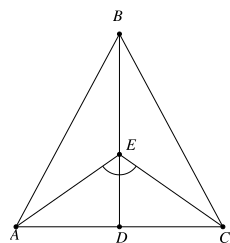
Cho hình vẽ dưới đây. Tam giác ABC cân tại B, D là trung điểm của AC. Biết \(\widehat {AEC} = 110^\circ \), tổng \(\widehat {ABE} + \widehat {BAE}\) là
Xem đáp án
Đáp án đúng là: C
Xét tam giác BAD và tam giác BCD có:
BA = BC (\(\Delta ABC\) cân tại B)
AD là cạnh chung
AD = CD (D là trung điểm của AC)
⇒ \(\Delta BAD = \Delta BCD\) (c.c.c)
⇒ \(\widehat {BDA} = \widehat {BDC}\) (hai góc tương ứng)
Mà \(\widehat {BDA} + \widehat {BDC} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {BDA} = \widehat {BDC} = 90^\circ \)
Xét tam giác ADE vuông tại D và tam giác CDE vuông tại D có:
AD = CD
DE là cạnh chung
⇒ \(\Delta ADE = \Delta CDE\) (hai cạnh góc vuông)
⇒ \(\widehat {AED} = \widehat {CED}\) (hai góc tương ứng)
Mà \(\widehat {AEC} = 110^\circ \)
⇒ \(\widehat {AED} = \widehat {CED} = \frac{{\widehat {AEC}}}{2} = 55^\circ \)
Ta có góc AED là góc ngoài tại đỉnh E của tam giác ABE nên
\(\widehat {ABE} + \widehat {BAE} = \widehat {AED} = 55^\circ \)
Câu 12:
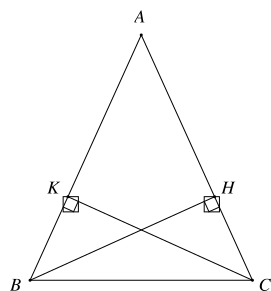
Cho hình vẽ dưới đây, biết tam giác ABC cân tại A. Khẳng định sai là
Xem đáp án
Đáp án đúng là: A
Tam giác ABC cân tại A ⇒ AB = AC và \(\widehat {ABC} = \widehat {ACB}\) (tính chất tam giác cân)
Xét tam giác BHA (vuông tại H) và tam giác CKA (vuông tại K) có:
AB = AC (\(\Delta ABC\) cân tại A)
\(\widehat A\) là góc chung
⇒ \(\Delta BHA = \Delta CKA\) (cạnh huyền – góc nhọn)
⇒ BH = CK (hai cạnh tương ứng)
Vậy khẳng định A sai.
Câu 13:
Cho tam giác ABC cân tại A. I là trung điểm của đoạn thẳng BC.
Khẳng định đúng nhất là
Xem đáp án
Đáp án đúng là: D
Xét tam giác AIB và tam giác AIC có:
AB = AC (\(\Delta ABC\) cân tại A)
BI = CI (theo giả thiết)
AI là cạnh chung
⇒ \(\Delta AIB = \Delta AIC\) (c.c.c)
⇒ \(\widehat {AIB} = \widehat {AIC}\) (hai góc tương ứng)
Mà \(\widehat {AIB} + \widehat {AIC} = 180^\circ \)
⇒ \(\widehat {AIB} = \widehat {AIC} = 90^\circ \)
⇒ AI ⊥ BC
Vì \(\Delta AIB = \Delta AIC\) (chứng minh trên)
⇒ \(\widehat {IAB} = \widehat {IAC}\) (hai góc tương ứng)
⇒ AI là tia phân giác của góc BAC
Câu 14:
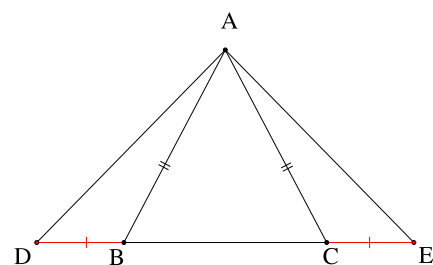
Cho hình vẽ dưới đây, biết tam giác ABC cân tại A và BD = CE. Khẳng định đúng là
Xem đáp án
Đáp án đúng là: C
\(\Delta ABC\) cân tại A ⇒ \(\widehat {ABC} = \widehat {ACB}\) (tính chất)
Mà: \(\widehat {ABC} + \widehat {ABD} = 180^\circ \) (hai góc kề bù
\(\widehat {ACB} + \widehat {ACE} = 180^\circ \) (hai góc kề bù)
⇒ \(\widehat {ABD} = \widehat {ACE}\)
Xét tam giác ADB và tam giác AEC có:
AB = AC (\(\Delta ABC\) cân tại A)
\(\widehat {ABD} = \widehat {ACE}\) (chứng minh trên)
BD = CE (theo giả thiết)
⇒ \(\Delta ADB = \Delta AEC\) (c.g.c)
⇒ AD = AE (hai cạnh tương ứng)
⇒ \(\Delta ADE\) cân tại A
Câu 15:
Cho tam giác ABC cân tại A có AH là đường phân giác của góc BAC (H ∈ BC). Khẳng định sai là
Xem đáp án
Đáp án đúng là: D
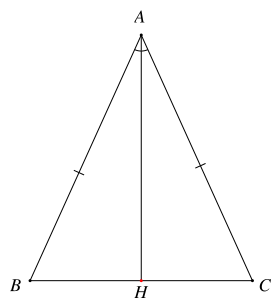
Xét tam giác ABH và tam giác ACH có:
AB = AC (\(\Delta ABC\) cân tại A)
\(\widehat {BAH} = \widehat {CAH}\) (AH là đường phân giác của \(\widehat {BAC}\))
AH là cạnh chung
⇒ \(\Delta ABH = \Delta ACH\) (c.g.c)
⇒ HB = HC (hai cạnh tương ứng) (1)
Và \(\widehat {AHB} = \widehat {AHC}\) (hai góc tương ứng)
Mà \(\widehat {AHB} + \widehat {AHC} = 180^\circ \) (hai góc kề bù)
⇒ \(\widehat {AHB} = \widehat {AHC} = 90^\circ \) ⇒ AH ⊥ BC (2)
Từ (1) và (2) ⇒ AH là đường trung trực của đoạn thẳng BC