Trắc nghiệm Toán 7 CTST Bài 8. Tính chất ba đường cao của tam giác có đáp án (Phần 2)
Trắc nghiệm Toán 7 CTST Bài 8. Tính chất ba đường cao của tam giác có đáp án (Phần 2) (Thông hiểu)
-
276 lượt thi
-
7 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác MNP có ˆM=63∘,ˆN=48∘. Vẽ trực tâm O của tam giác MNP. Số đo góc MON là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Gọi giao điểm của NO và PM là A, giao điểm của MO và PN là B
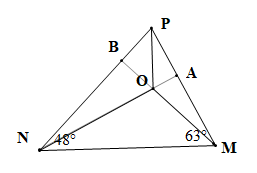
Vì O là trực tâm tam giác MNP nên NA ⊥ PM, MB ⊥ PN.
Vì DMNA vuông tại A nên ^ANM+^AMN=90∘ (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Suy ra ^ANM=90∘−^AMN=90∘−63∘=27∘.
Vì DMNB vuông tại B nên ^BNM+^BMN=90∘ (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Suy ra ^BMN=90∘−^BNM=90∘−48∘=42∘.
Xét DOMN có ^ONM+^OMN+^MON=180∘ (tổng ba góc trong một tam giác)
Suy ra ^MON=180∘−^ONM−^OMN=180∘−27∘−42∘=111∘.
Vậy ta chọn phương án A.
Câu 2:
Cho tam giác ABC nhọn có đường cao AI. Trên AI lấy E sao cho ^BAI=^BCE. Gọi F là giao điểm của AB và CE, H là giao điểm của BE và AC. Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
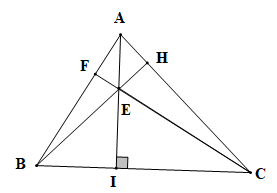
Vì DABI vuông tại I nên ^BAI+^ABI=90∘(trong tam giác vuông tổng hai góc nhọn bằng 90°)
Xét DBCF có ^BCF+^BFC+^FBC=180∘ (tổng ba góc trong một tam giác)
Mà ^BAI=^BCF nên ^BAI+^BFC+^ABI=180∘
Suy ra ^BFC=180∘−(^BAI+^ABI)=180∘−90∘=90∘.
Do đó phương án A là đúng.
Vì ^BFC=90∘ nên CF ⊥ AB.
Xét DABC có AI, CF là hai đường cao cắt nhau tại E nên E là trực tâm tam giác ABC.
Do đó BH ⊥ AC. Do đó B và C là đúng.
Vậy ta chọn phương án D.
Câu 3:
Cho tam giác ABC có ˆB=50∘,ˆC=30∘. Vẽ đường cao AH, phân giác AE. Trên cạnh AC lấy D sao cho ^CBD=10∘. Gọi I là giao điểm của AE và BD. Số đo góc AID là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
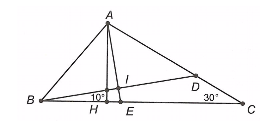
Xét DBCD có ^BCD+^BDC+^CBD=180∘ (tổng ba góc trong một tam giác)
Suy ra ^BDC=180∘−^BCD−^CBD=180∘−30∘−10∘=140∘.
Ta có ^ADB+^BDC=180∘(hai góc kề bù)
Nên ^ADB=180∘−^BDC=180∘−140∘=40∘.
Ta có ^ABD+^DBC=^ABC (hai góc kề nhau)
Suy ra ^ABD=^ABC−^DBC=50∘−10∘=40∘.
Xét DABD có ^ABD=^ADB(=40∘) nên tam giác ABD cân tại A.
Mà AI là tia phân giác của góc BAD nên đồng thời là đường cao.
Hay AI ⊥ BD
Do đó ^AID=90∘
Vậy ta chọn phương án D.
Câu 4:
Cho tam giác XYZ nhọn, đường cao XA. Lấy B thuộc đoạn AZ, vẽ BC vuông góc XZ. Giao điểm của XA và BC là I. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
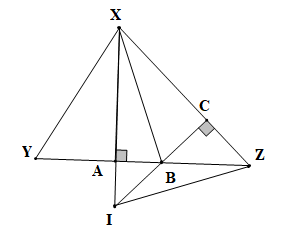
Vì DXYZ nhọn nên ^YXZ<90∘, do đó B là khẳng định sai.
Vì CB ⊥ XZ, ^YXZ<90∘nên XY và IC không song song với nhau.
Do đó A là khẳng định sai.
Xét DIXZ có IC, ZA là hai đường cao cắt nhau tại B nên B là trực tâm tam giác XIZ.
Do đó XB ⊥ IZ, nên C là khẳng định đúng.
Vậy ta chọn phương án C.
Câu 5:
Cho tam giác ABC vuông tại A, trên tia BA lấy M sao cho BM = BC. Tia phân giác góc B cắt AC tại H. Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
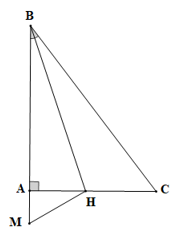
• Xét ΔBHM và ∆BHC có:
BH là cạnh chung,
^ABH=^CBH (do BH là tia phân giác của góc ABC),
BM = BC (giả thiết)
Do đó ΔBHM = ∆BHC (c.g.c)
Suy ra MH = HC (hai cạnh tương ứng), nên C là khẳng định đúng.
• Vì BM = BC và HM = HC nên BH là đường trung trực của MC.
Do đó BH ⊥ MC hay BH là đường cao của tam giác MBC.
Khi đó A là khẳng định đúng.
• Xét DBMC có hai đường cao BH và CA cắt nhau tại H nên H là trực tâm tam giác BMC.
Do đó MH ⊥ BC nên khẳng định B là đúng.
Vậy ta chọn phương án D.
Câu 6:
Cho tam giác IHK đều có G là trọng tâm. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
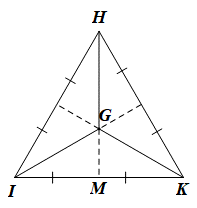
Gọi M là trung điểm của IK.
• Xét DHIM và DHKM có:
HI = HK (do DIHK đều),
HM và cạnh chung,
IM = KM (do M là trung điểm của IK).
Do đó DHIM = DHKM (c.c.c).
Suy ra ^HMI=^HMK (hai góc tương ứng).
Mà ^HMI+^HMK=180∘ (hai góc kề bù)
Nên ^HMI=^HMK=180∘2=90∘ hay HG ⊥ IK.
Chứng minh tương tự ta cũng có IG ⊥ HK và KG ⊥ IH.
• Xét DHIG có HK ⊥ IG, IK ⊥ HG, KG ⊥ HI.
Nên HK, IK, KG là ba đường cao của tam giác HIG.
Mà HK, IK, KG cắt nhau tại K.
Suy ra K là trực tâm tam giác GIH.
Vậy ta chọn phương án C.
Câu 7:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
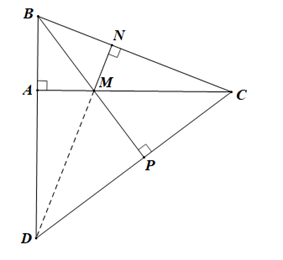
• Xét ∆DBC có CA, BP là hai đường cao cắt nhau tại M nên M là trực tâm của ∆DBC.
Do đó phương án A đúng.
• Vì M là trực tâm của ∆DBC nên DM ⊥ BC.
Do đó phương án B đúng.
• Ta có DM ⊥ BC (chứng minh trên).
Mà MN ⊥ BC (giả thiết).
Suy ra D, M, N thẳng hàng.
Do đó phương án C đúng.
• Ta có:
+) D ∈ MN (do D, M, N thẳng hàng);
+) D ∈ AB (giả thiết);
+) D ∈ CP (giả thiết).
Suy ra AB, MN, CP cùng đồng quy tại điểm D.
Do đó phương án D sai.
Vậy ta chọn phương án D.
