7 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 7 CD Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc

Trắc nghiệm Toán 7 Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh có đáp án

Trắc nghiệm Toán 7 CD Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (Thông hiểu) có đáp án

217 lượt thi
7 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho tam giác ABC và tam giác DEF có AB = DE, AC = DF, $\hat{A} = \hat{D}$ . Biết $\hat{B} = 60 °$ . Số đo góc E là

A. 90°;

B. 30°;

C. 60°;

D. 120°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Xét ∆ABC và ∆DEF có:

AB = DE

$\hat{A} = \hat{D}$

AC = DF

Do đó, ∆ABC = ∆DEF (c.g.c)

Suy ra: $\hat{B} = \hat{E}$ (hai góc tương ứng)

Mà $\hat{B} = 60 ° \Rightarrow \hat{E} = 60 °$ .

Câu 2:

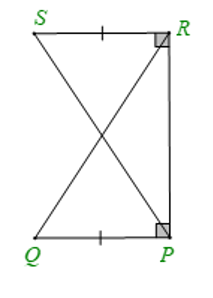
Cho hình vẽ dưới đây. Khẳng định đúng là

A. $Δ S R P = Δ Q P R$ ;

B. $Δ S R P = Δ Q R P$ ;

C. $Δ S R P = Δ P R Q$ ;

Δ S R P = Δ P Q R

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Hai tam giác SRP (vuông tại R) và tam giác QPR (vuông tại P) có:

RP là cạnh chung

SR = QP

Nên $Δ S R P = Δ Q P R$ (hai cạnh góc vuông).

(Đỉnh S tương ứng với đỉnh Q; đỉnh R của tam giác này tương ứng với đỉnh P của tam giác kia và ngược lại).

Câu 3:

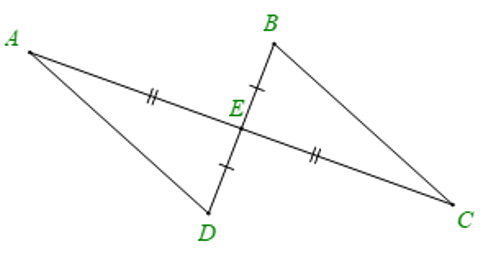
Cho hình vẽ dưới đây, biết AE = CE, DE = BE. Khẳng định đúng là

A. $Δ A E D = Δ C B E$ ;

B. $Δ A E D = ∆ B E C$ ;

C. $Δ A E D = Δ E B C$ ;

Δ A E D = Δ C E B

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Hai tam giác AED và CEB có:

AE = CE

$\hat{A E D} = \hat{C E B}$ (hai góc đối đỉnh)

DE = BE

Do đó $Δ A E D = Δ C E B$ (c.g.c).

Câu 4:

Cho tam giác ABC vuông tại A và tam giác PMN vuông tại P có AB = PM, AC = PN. Biết $\hat{B} = 60 °$ . Số đo góc N là

A. 60°;

B. 90°;

C. 30°;

D. 50°.

Xem đáp án

Cho tam giác ABC vuông tại A và tam giác PMN vuông tại P có AB = PM, AC = PN. (ảnh 1)

Câu 5:

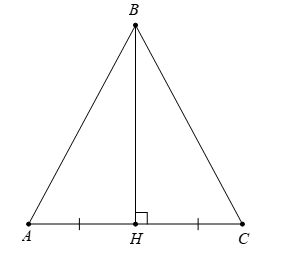
Cho hình vẽ dưới đây. Khẳng định sai là

A. BA = BC;

B. BH là tia phân giác góc ABC;

C. ∆ABH = ∆HBC;

\hat{A} = \hat{C}

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Xét tam giác ABH vuông tại H và tam giác CBH vuông tại H có:

AH = CH

BH là cạnh chung

Nên ∆ABH = ∆CBH (2 cạnh góc vuông) (C sai)

Suy ra BA = BC (hai cạnh tương ứng) (A đúng)

$\hat{A} = \hat{C}$ (hai góc tương ứng) (D đúng)

$\hat{A B H} = \hat{C B H}$ (hai góc tương ứng) nên BH là tia phân giác góc ABC. (B đúng)

Câu 6:

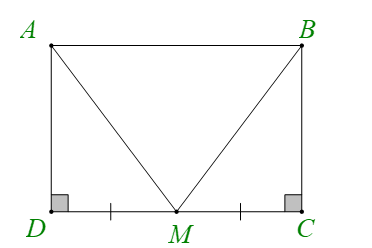
Cho hình chữ nhật ABCD, M là trung điểm của cạnh CD. Khẳng định sai là

A. $Δ A D M = Δ B C M$ ;

B. AD = BM;

C. AD = BC;

\hat{A M D} = \hat{B M C}

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

ABCD là hình chữ nhật ⇒ AD = BC và $\hat{A D M} = \hat{B C M} = 90 °$ .

Xét hai tam giác vuông ADM và BCM có:

AD = BC (chứng minh trên)

DM = CM (giả thiết)

⇒ $Δ A D M = Δ B C M$ (hai cạnh góc vuông)

⇒ AD = BC; AM = BM (các cạnh tương ứng)

$\hat{A M D} = \hat{B M C}$ (hai góc tương ứng)

Vậy khẳng định B sai.

Câu 7:

Cho hình vẽ dưới đây, biết CE = DE và $\hat{C E A} = \hat{D E A}$ .

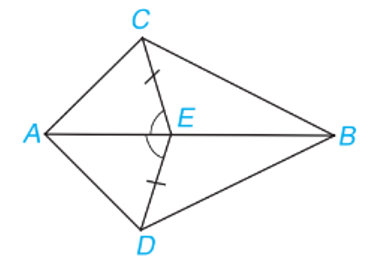
Cho hình vẽ dưới đây, biết CE = DE và góc CEA= góc DEA. (ảnh 1)

Khẳng định sai là

A. ∆AEC = ∆AED ;

B. AC = AD;

C. AE là tia phân giác của góc CAD;

\hat{A C B} = \hat{A B D}

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Xét ∆AEC và ∆AED có:

CE = DE (theo giả thiết)

$\hat{C E A} = \hat{D E A}$ (theo giả thiết)

AE là cạnh chung

Do đó ∆AEC = ∆AED (c.g.c)

⇒ AC = AD (2 cạnh tương ứng)

và $\hat{C A E} = \hat{D A E}$ (2 góc tương ứng) nên AE là tia phân giác của góc CAD.

Xét $Δ A B C$ và $Δ A B D$ có:

AC = AD (chứng minh trên)

$\hat{C A E} = \hat{D A E}$ (chứng minh trên)

AB là cạnh chung

Do đó ∆ABC = ∆ABD (c.g.c)

⇒ $\hat{A C B} = \hat{A D B}$ (2 góc tương ứng)

Vậy khẳng định D sai.

Bắt đầu thi ngay

Trắc nghiệm Toán 7 Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh có đáp án

Trắc nghiệm Toán 7 CD Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (Thông hiểu) có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương