Dạng 2. Chứng minh các bất đẳng thức về độ dài cạnh của tam giác
-
208 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác HKQ có QH < QK < HK. Bất đẳng thức nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
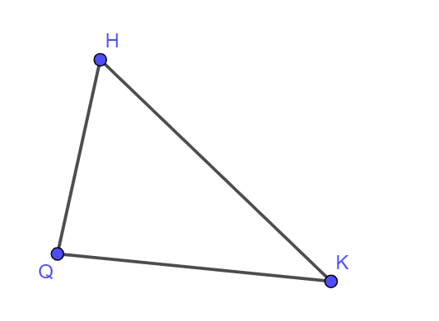
Áp dụng bất đẳng thức tam giác cho ∆HKQ, ta có:
⦁ QK – QH < HK < QK + QH;
⦁ HK – QH < QK < HK + QH;
Vậy bất đẳng thức QK < HK + QH là đúng.
Câu 2:
Chọn đáp án đúng. Trong một tam giác
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là:A
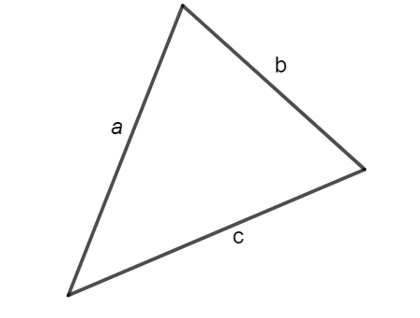
Xét tam giác có độ dài ba cạnh lần lượt là a, b, c (a, b, c > 0).
Áp dụng bất đẳng thức tam giác, ta có: a < b + c.
Do đó a + a < b + c + a (chu vi của tam giác)
Suy ra 2a < a + b + c
Hay a < (a + b + c) : 2 (nửa chu vi của tam giác)
Tương tự với cạnh b và c.
Vậy phương án đúng là A
Câu 3:
Cho tam giác DEF có DE < EF < DF. Bất đẳng thức nào dưới đây là sai?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
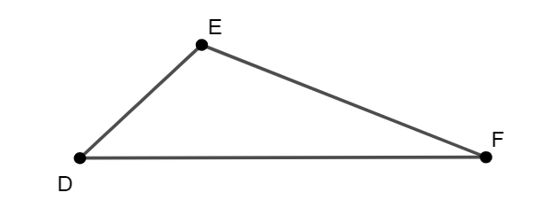
Bất đẳng thức ở phương án D sai do trong tam giác, độ dài cạnh bất kì luôn lớn hơn hiệu độ dài hai cạnh còn lại. Vì vậy DF – EF < DE.
Câu 4:
Cho tam giác MNP có MP > MN > NP. Bất đẳng thức nào dưới đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
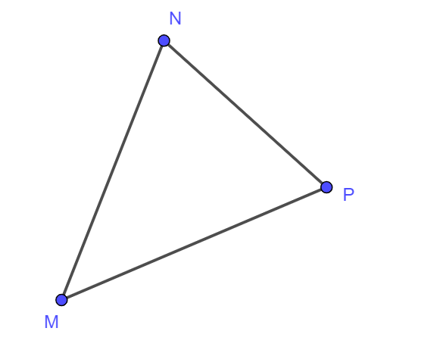
Áp dụng bất đẳng thức cho ∆MNP ta có:
⦁ MP – MN < NP. Do đó A sai.
⦁ MP – NP < MN < MP + NP. Do đó B đúng.
⦁ MN – NP < MP < MN + NN. Do đó C sai.
Vậy ta chọn phương án B.
Câu 5:
Cho ∆ABC có M là trung điểm của BC. Bất đẳng thức nào dưới đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
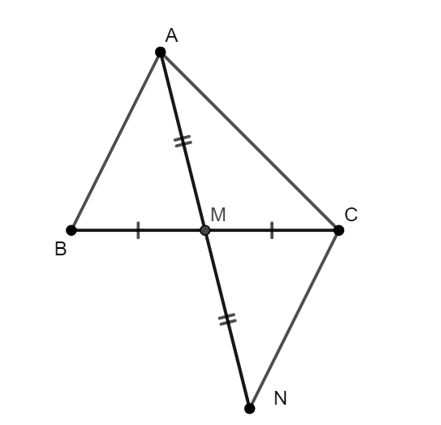
Trên tia đối của tia AM lấy N sao cho MN = MA.
Xét ∆MAB và ∆MNC có:
MA = MN (theo cách vẽ);
( hai góc đối đỉnh)
MB = MC (do M là trung điểm của BC)
Do đó ∆MAB = ∆MNC (c.g.c)
Suy ra AB = NC (hai cạnh tương ứng) (1)
Xét ∆ACN có: AC + CN > AN (bất đẳng thức tam giác) (2)
Từ (1) và (2) ta có AC + AB > AN
Mặt khác MN = MA, suy ra AN = 2AM
Do đó AC + AB > 2AM.
C có M là trung điểm của BC. Bất đẳng thức nào dưới đây là đúng?
Câu 6:
Cho tam giác ABC có đường cao AH (H ∈ BC). Bất đẳng thức nào dưới đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
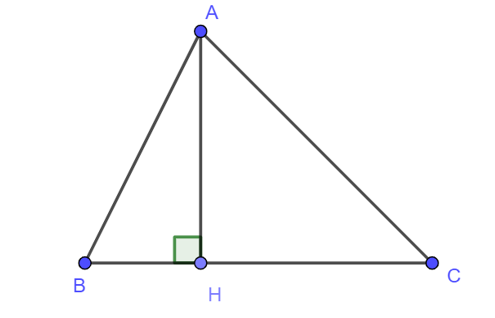
Xét ∆AHB có AH + HB > AB (bất đẳng thức tam giác) (1)
Xét ∆AHC có AH + HC > AC (bất đẳng thức tam giác) (2)
Cộng vế theo vế của (1) với (2) ta được AH + HB + AH + HC > AB + AC
Suy ra 2AH + HB + HC > AB + AC
Mà HB + HC = BC (do H ∈ BC)
Suy ra 2AH + BC > AB + AC.
Câu 7:
Cho tam giác OBC cân ở O. Trên tia đối của tia OC lấy điểm A (A khác O). Bất đẳng thức nào dưới đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
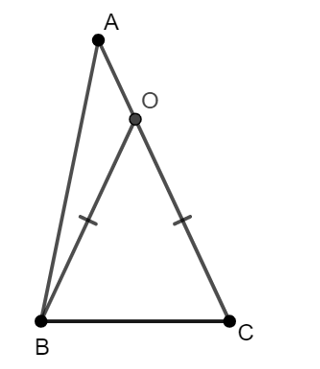
Xét ∆ABO có AB < BO + OA (bất đẳng thức tam giác)
Mà ∆BOC cân tại O nên OB = OC
Suy ra AB < OC + OA
Lại có OC + OA = AC nên AB < AC.
Câu 8:
Cho tam giác OBC cân ở O. Trên tia đối của tia CO lấy điểm A (A khác O). Bất đẳng thức nào dưới đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
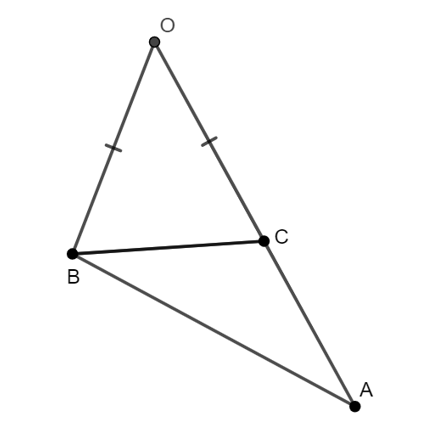
Xét ∆ABO có AB > OA – OB (bất đẳng thức tam giác)
Mà ∆BOC cân tại O nên OB = OC
Suy ra AB < OA – OC
Lại có OA – OC = AC nên AB > AC.
Câu 9:
Cho hình vẽ dưới đây
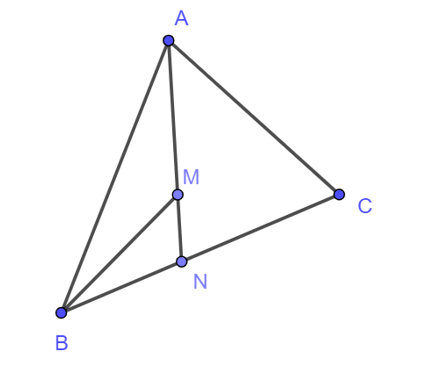
Bất đẳng thức nào dưới đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Xét ∆MNB có: MB < MN + NB (bất đẳng thức tam giác)
Do đó MA + MB < MA + MN + NB.
Mà MA + MN = NA nên ta có MA + MB < NA + NB (1)
Xét ∆NAC có: NA < AC + CN (bất đẳng thức tam giác)
Do đó NA + NB < AC + CN + NB.
Mà NB + NC = BC nên ta có NA + NB < AC + BC (2)
Từ (1) và (2) ta có MA + MB < NA + NB < AC + BC.
Do đó MA + MB < AC + BC.
Câu 10:
Cho tam giác ABC nhọn có AB < AC. Trên đường phân giác AD lấy điểm E (E thuộc cạnh AD). Khẳng định nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là:B
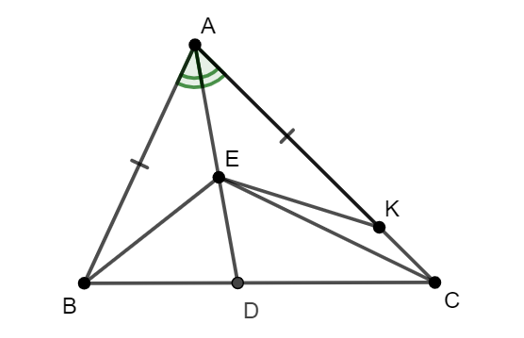
Trên cạnh AC lấy điểm K sao cho AB = AK.
Xét ∆BAE và ∆KAE có:
AB = AK;
(do AD là tia phân giác của
Cạnh AE chung
Do đó ∆BAE = ∆KAE (c.g.c).
Suy ra EB = EK (hai cạnh tương ứng).
Xét ∆CEK có: EC – EK < CK (bất đẳng thức tam giác)
Suy ra EC – EB < CK (1)
Mặt khác CK = AC – AK = AC – AB (do AB = AK theo cách dựng) (2)
Từ (1) và (2) ta có EC – EB < AC – AB.