Trắc nghiệm Toán 7 Bài 3. Hai đường thẳng song song có đáp án (Vận dụng)
-
256 lượt thi
-
3 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho hình vẽ
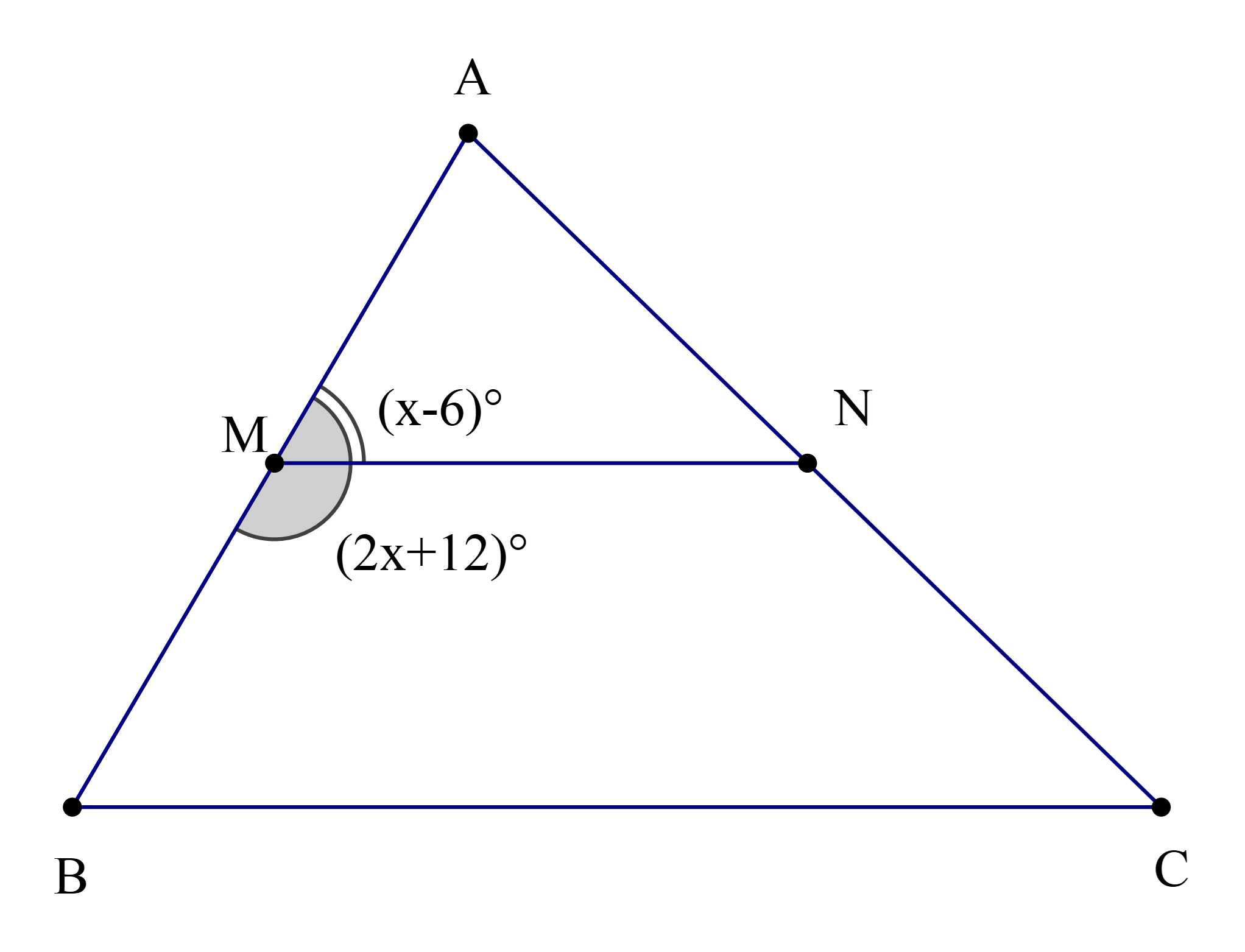
Biết rằng MN // BC. Số đó của ^ABC là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có ^AMN+^NMB=180∘ (hai góc kề bù)
Nên (x – 6)° + (2x + 12)° = 180°
Do đó (x – 6 + 2x + 12)° = 180°
Suy ra x – 6 + 2x + 12 = 180
Hay 3x = 180 + 6 – 12 = 174
Suy x = 58
Do đó ^AMN=(x−6)∘=(58−6)∘=52∘
Vì MN // BC nên ^AMN=^MBC=52∘ (hai góc đồng vị)
Hay ^ABC=52∘
Vậy ta chọn phương án A.
Câu 2:
Cho hình vẽ
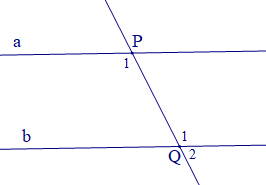
Biết rằng a // b và 2ˆQ2−ˆP1=12∘. Số đo của ˆQ2 là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có a // b nên ˆP1=ˆQ1 (hai góc so le trong)
Mà ˆQ1+ˆQ2=180∘ (hai góc kề bù)
Suy ra ˆQ2=180∘−ˆQ1
Ta lại có: 2ˆQ2−ˆP1=12∘
Suy ra 2(180∘−ˆQ1)−ˆQ1=12∘
Hay 360∘−2ˆQ1−ˆQ1=12∘
Do đó 3ˆQ1=348∘
Suy ra ˆQ1=348∘3=116∘
Khi đó ˆQ2=180∘−ˆQ1=180∘−116∘=64∘.
Vậy ta chọn phương án D.
Câu 3:
Cho hình vẽ:
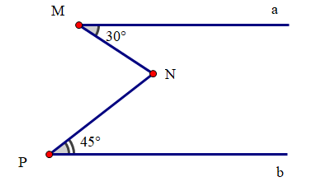
Biết Ma // Pb. Số đo ^MNP là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
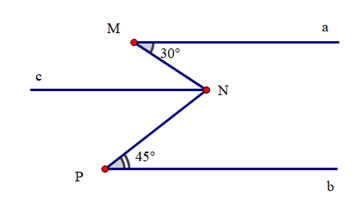
Kẻ Nc // Ma.
Suy ra ^aMN=^MNc=30∘(hai góc so le trong)
Ta có Nc // Ma, mà Ma // Pb
Suy ra Pb // Nc (vì cùng song song với Ma)
Suy ra ^NPb=^cNP=45∘ (hai góc so le trong)
Ta có ^MNP=^MNc+^cNP (hai góc kề bù)
Do đó ^MNP = 30° + 45° = 75°.
Vậy ta chọn phương án C.