Câu hỏi:
01/02/2024 67Cho hình vẽ
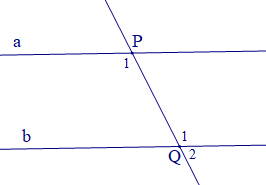
Biết rằng a // b và 2ˆQ2−ˆP1=12∘. Số đo của ˆQ2 là:
A. 61°;
B. 62°;
C. 63°;
D. 64°.
Đáp án chính xác
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Ta có a // b nên ˆP1=ˆQ1 (hai góc so le trong)
Mà ˆQ1+ˆQ2=180∘ (hai góc kề bù)
Suy ra ˆQ2=180∘−ˆQ1
Ta lại có: 2ˆQ2−ˆP1=12∘
Suy ra 2(180∘−ˆQ1)−ˆQ1=12∘
Hay 360∘−2ˆQ1−ˆQ1=12∘
Do đó 3ˆQ1=348∘
Suy ra ˆQ1=348∘3=116∘
Khi đó ˆQ2=180∘−ˆQ1=180∘−116∘=64∘.
Vậy ta chọn phương án D.
Hướng dẫn giải
Đáp án đúng là: D
Ta có a // b nên ˆP1=ˆQ1 (hai góc so le trong)
Mà ˆQ1+ˆQ2=180∘ (hai góc kề bù)
Suy ra ˆQ2=180∘−ˆQ1
Ta lại có: 2ˆQ2−ˆP1=12∘
Suy ra 2(180∘−ˆQ1)−ˆQ1=12∘
Hay 360∘−2ˆQ1−ˆQ1=12∘
Do đó 3ˆQ1=348∘
Suy ra ˆQ1=348∘3=116∘
Khi đó ˆQ2=180∘−ˆQ1=180∘−116∘=64∘.
Vậy ta chọn phương án D.