Trắc nghiệm Toán 7 Bài 12. Tổng các góc trong một tam giác có đáp án
Trắc nghiệm Toán 7 Bài 12. Tổng các góc trong một tam giác có đáp án
-
105 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Tổng ba góc trong một tam giác bằng
Xem đáp án
Đáp án đúng là: D
Tổng ba góc trong một tam giác bằng 180°.
Câu 2:
Cho tam giác ABC, khi đó \(\widehat A + \widehat B + \widehat C\) bằng
Xem đáp án
Đáp án đúng là: D
Tổng ba góc trong một tam giác bằng 180°.
Mà các góc A, B, C là ba góc trong cùng một tam giác ABC nên \(\widehat A + \widehat B + \widehat C = 180^\circ \)
Câu 3:
Cho \[\Delta ABC\] vuông tại A. Khi đó
Xem đáp án
Đáp án đúng là: A
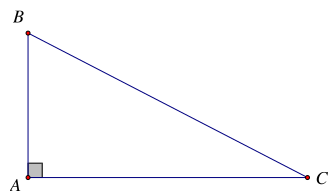
Tam giác ABC vuông tại A thì \(\widehat A = 90^\circ \)
Mà \(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng 3 góc trong tam giác)
⇒ \(90^\circ + \widehat B + \widehat C = 180^\circ \)
⇒ \(\widehat B + \widehat C = 90^\circ \)
Câu 4:
Cho \[\Delta ABC\] có \[\widehat A + \widehat C = 90^\circ \]. Khi đó \[\Delta ABC\] là
Xem đáp án
Đáp án đúng là: B
Xét tam giác ABC có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng 3 góc trong tam giác)
Mà \[\widehat A + \widehat C = 90^\circ \] ⇒ \(\widehat B = 90^\circ \)
⇒ Tam giác ABC vuông tại B.
Câu 5:
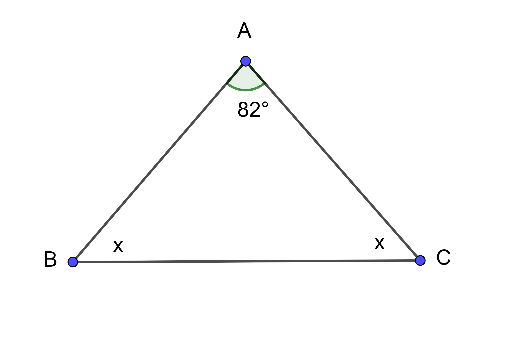
Cho hình vẽ sau, số đo x là
Xem đáp án
Đáp án đúng là: B
Xét tam giác ABC có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng 3 góc trong tam giác)
⇒ \(82^\circ + x + x = 180^\circ \)
⇒ \(2x = 180^\circ - 82^\circ \)
⇒ \(2x = 98^\circ \)
⇒ \(x = 49^\circ \)
Câu 6:
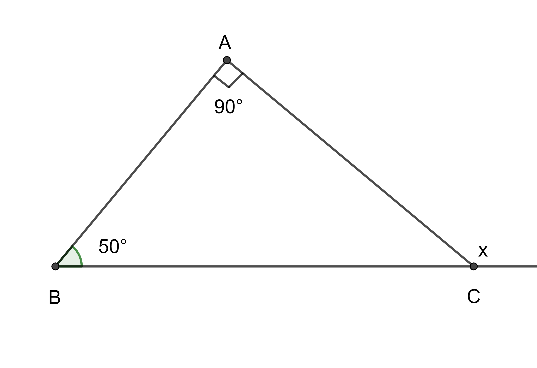
Cho hình vẽ sau. Số đo x bằng
Xem đáp án
Đáp án đúng là: D
Ta có: \(x = \widehat A + \widehat B\) (góc ngoài của tam giác)
⇒ \(x = 90^\circ + 50^\circ \)
⇒ \(x = 140^\circ \)
Câu 7:
Cho \[\Delta ABC\] có 3 góc bằng nhau. Số đo mỗi góc là
Xem đáp án
Đáp án đúng là: D
Xét tam giác ABC có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng 3 góc trong tam giác)
Mà \(\widehat A = \widehat B = \widehat C\)
⇒ \(\widehat A = \widehat B = \widehat C = \frac{{180^\circ }}{3} = 60^\circ \)
Câu 8:
Cho \[\Delta ABC\] có \[\widehat A = 100^\circ \], \[\widehat B - \widehat C = 40^\circ \]. Số đo góc B và C lần lượt là
Xem đáp án
Đáp án đúng là: A
Xét tam giác ABC có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng 3 góc trong tam giác)
Mà \[\widehat A = 100^\circ \]
⇒ \(100^\circ + \widehat B + \widehat C = 180^\circ \)
⇒ \(\widehat B + \widehat C = 80^\circ \)
Lại có: \[\widehat B - \widehat C = 40^\circ \]
⇒ \(\widehat B = \left( {80^\circ + 40^\circ } \right):2 = 60^\circ \)
⇒ \(\widehat C = 80^\circ - 60^\circ = 20^\circ \)
Câu 9:
Cho \[\Delta ABC\] có \[\widehat A = 60^\circ \], \[\widehat B = \frac{1}{3}\widehat C\]. Số đo góc B là
Xem đáp án
Đáp án đúng là: D
Xét tam giác ABC có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng 3 góc trong tam giác)
Mà \[\widehat A = 60^\circ \].
⇒ \(60^\circ + \widehat B + \widehat C = 180^\circ \)
⇒ \(\widehat B + \widehat C = 120^\circ \)
Lại có: \[\widehat B = \frac{1}{3}\widehat C\]
⇒ \(\widehat B = 120^\circ :\left( {1 + 3} \right) \cdot 1 = 30^\circ \)
Câu 10:
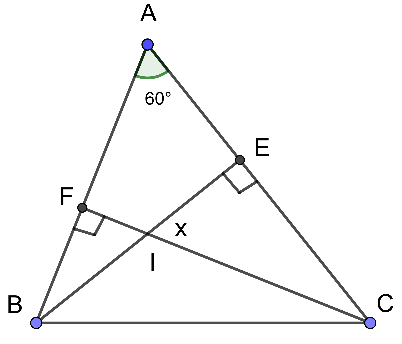
Cho hình vẽ sau. Số đo góc x bằng
Xem đáp án
Đáp án đúng là: C
Xét \[\Delta ACF\]có:
\[\widehat A + \widehat {ACF} + \widehat {AFC} = 180^\circ \] (tổng ba góc trong một tam giác)
⇒ \[60^\circ + \widehat {ACF} + 90^\circ = 180^\circ \]
⇒ \[\widehat {ACF} = 180^\circ - 60^\circ - 90^\circ \]
⇒ \[\widehat {ACF} = 30^\circ \]
Xét \[\Delta IEC\] ta có:
\[\widehat {IEC} + \widehat {ECI} + \widehat {EIC} = 180^\circ \]. (tổng ba góc trong một tam giác)
⇒ \[30^\circ + x + 90^\circ = 180^\circ \]
⇒ \[x = 180^\circ - 90^\circ - 30^\circ \]
⇒ \[x = 60^\circ \]
Câu 11:
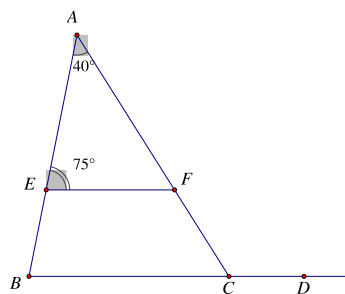
Cho hình vẽ dưới đây, biết \(FE{\rm{//}}BD\). Số đo góc FCD là
Xem đáp án
Đáp án đúng là: A
Vì \(FE{\rm{//}}BD\) ⇒ \(\widehat {ABC} = \widehat {AEF}\) (hai góc đồng vị)
Mà \(\widehat {AEF} = 75^\circ \) ⇒ \(\widehat {ABC} = 75^\circ \)
Ta có: \(\widehat {FCD}\) là góc ngoài tại đỉnh C của tam giác ABC nên
\(\widehat {FCD} = \widehat A + \widehat {ABC}\)
\(\widehat {FCD} = 40^\circ + 75^\circ \)
\(\widehat {FCD} = 115^\circ \)
Câu 12:
Cho \[\Delta ABC\] có \[\widehat A = 30^\circ \], \[\widehat B - \widehat C = 30^\circ \]. Tam giác ABC là
Xem đáp án
Đáp án đúng là: A
Xét tam giác ABC có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng 3 góc trong tam giác)
Mà \[\widehat A = 30^\circ \]
⇒ \(30^\circ + \widehat B + \widehat C = 180^\circ \)
⇒ \(\widehat B + \widehat C = 150^\circ \)
Lại có: \[\widehat B - \widehat C = 30^\circ \]
⇒ \(\widehat B = \left( {150^\circ + 30^\circ } \right):2 = 90^\circ \)
Tam giác ABC có góc B bằng 90° nên tam giác ABC vuông tại B.
Câu 13:
Cho tam giác ABC vuông tại A, tia phân giác góc B cắt AC tại D. Biết \(\widehat {ABC} = 60^\circ \). Số đo góc BDC là
Xem đáp án
Đáp án đúng là: B
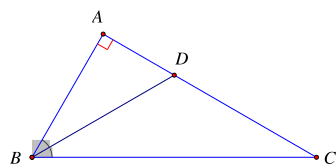
Cho tam giác ABC vuông tại A nên \(\widehat A = 90^\circ \)
Vì BD là tia phân giác góc ABC nên
\[\widehat {ABD} = \frac{{\widehat {ABC}}}{2} = \frac{{60^\circ }}{2} = 30^\circ \]
\[\widehat {BDC}\] là góc ngoài của đỉnh D của \[\Delta ABD\] nên
\[\widehat {BDC}\] = \[\widehat {ABD} + \widehat A = 30^\circ + 90^\circ = 120^\circ \]
Câu 14:
Cho \[\Delta ABC\] vuông tại A. Tia phân giác của góc B cắt AC tại E. Hãy chọn đáp án đúng.
Xem đáp án
Đáp án đúng là: C
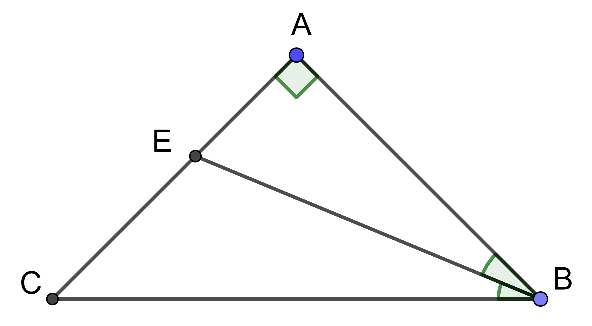
\[\widehat {BEC}\] là góc ngoài của đỉnh E của \[\Delta AEB\] nên
\[\widehat {BEC} = \widehat A + \widehat {ABE} = 90^\circ + \widehat {EBA}\]
⇒ \[\widehat {BEC} > \widehat {EBA}\] Do đó, D sai
Và \[\widehat {BEC} > 90^\circ \]
⇒ Tam giác BEC là tam giác tù. (C đúng; A, B sai)
Câu 15:
Cho \[\Delta ABC\] có \[\widehat A = 50^\circ \], \[\widehat B = 70^\circ \]. Tia phân giác của góc C cắt cạnh AB tại M. Tính số đo các góc AMC, BMC.
Xem đáp án
Đáp án đúng là: D
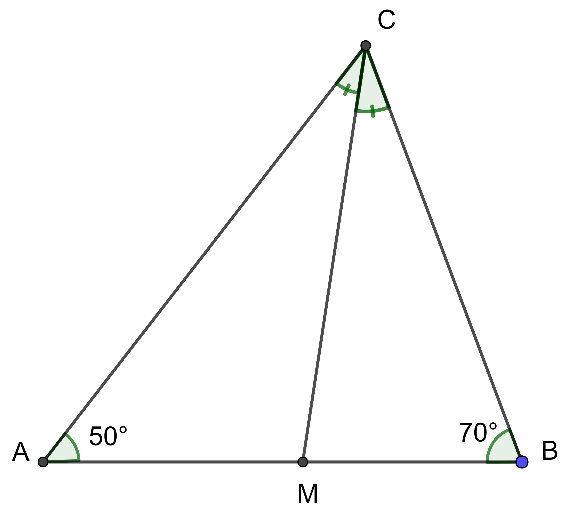
Xét
\[\Delta ABC\] có \[\widehat A + \widehat B + \widehat {BCA} = 180^\circ \] (tổng ba góc trong tam giác)
⇒ \[\widehat {BCA} = 180^\circ - \widehat A - \widehat B\]
⇒ \[\widehat {BCA} = 180^\circ - 50^\circ - 70^\circ \]
⇒ \[\widehat {BCA} = 60^\circ \]
Vì CM là tia phân giác góc BCA nên
\[\widehat {BCM} = \widehat {MCA} = \frac{{\widehat {BCA}}}{2} = \frac{{60^\circ }}{2} = 30^\circ \]
Ta có \[\widehat {AMC}\] là góc ngoài tại đỉnh M của \[\Delta MBC\] nên ta có:
\[\widehat {AMC} = \widehat B + \widehat {BCM} = 70^\circ + 30^\circ = 100^\circ \]
Lại có \[\widehat {AMC} + \widehat {BMC} = 180^\circ \] (hai góc kề bù)
⇒ \[\widehat {BMC} = 180^\circ - \widehat {AMC} = 180^\circ - 100^\circ = 80^\circ \]
Vậy \[\widehat {AMC} = 100^\circ \]; \[\widehat {BMC} = 80^\circ \].