Câu hỏi:
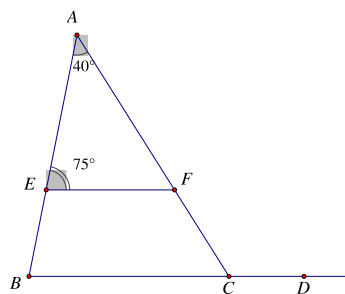
25/01/2024 57Cho hình vẽ dưới đây, biết \(FE{\rm{//}}BD\). Số đo góc FCD là
A. 115°;
B. 75°;
C. 65°;
D. 120°.
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
Vì \(FE{\rm{//}}BD\) ⇒ \(\widehat {ABC} = \widehat {AEF}\) (hai góc đồng vị)
Mà \(\widehat {AEF} = 75^\circ \) ⇒ \(\widehat {ABC} = 75^\circ \)
Ta có: \(\widehat {FCD}\) là góc ngoài tại đỉnh C của tam giác ABC nên
\(\widehat {FCD} = \widehat A + \widehat {ABC}\)
\(\widehat {FCD} = 40^\circ + 75^\circ \)
\(\widehat {FCD} = 115^\circ \)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Cho \[\Delta ABC\] có \[\widehat A = 30^\circ \], \[\widehat B - \widehat C = 30^\circ \]. Tam giác ABC là
Câu 5:
Cho \[\Delta ABC\] có \[\widehat A = 60^\circ \], \[\widehat B = \frac{1}{3}\widehat C\]. Số đo góc B là
Câu 6:
Cho \[\Delta ABC\] có \[\widehat A = 50^\circ \], \[\widehat B = 70^\circ \]. Tia phân giác của góc C cắt cạnh AB tại M. Tính số đo các góc AMC, BMC.
Câu 7:
Cho tam giác ABC, khi đó \(\widehat A + \widehat B + \widehat C\) bằng
Câu 10:
Cho \[\Delta ABC\] vuông tại A. Tia phân giác của góc B cắt AC tại E. Hãy chọn đáp án đúng.
Câu 12:
Cho tam giác ABC vuông tại A, tia phân giác góc B cắt AC tại D. Biết \(\widehat {ABC} = 60^\circ \). Số đo góc BDC là
Câu 13:
Cho \[\Delta ABC\] có \[\widehat A = 100^\circ \], \[\widehat B - \widehat C = 40^\circ \]. Số đo góc B và C lần lượt là
Câu 14:
Cho \[\Delta ABC\] có \[\widehat A + \widehat C = 90^\circ \]. Khi đó \[\Delta ABC\] là
