Trắc nghiệm Toán 6 KNTT Phép nhân số nguyên, phép chia hết bội và ước của một số nguyên có đáp án (Phần 2)
Trắc nghiệm Toán 6 KNTT Bài 22. Các dạng toán phép nhân, chia số nguyên, bội và ước của một số nguyên có đáp án
-
151 lượt thi
-
24 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Chọn câu sai
 Xem đáp án
Xem đáp án
Trả lời:
Đáp án A: \[( - 5).25 = - 125\] nên A đúng
Đáp án B: \[6.( - 15) = - 90\] nên B đúng
Đáp án C: \[125.\left( { - 20} \right) = - 2500 \ne - 250\] nên C sai
Đáp án D: \[225.( - 18) = - 4050\] nên D đúng.
Đáp án cần chọn là: C
Câu 2:
 Xem đáp án
Xem đáp án
Trả lời:
Áp dụng quy tắc nhân hai số nguyên cùng dấu ta có:
\[( - 42).( - 5) = 42.5 = 210\]
Đáp án cần chọn là: B
Câu 3:
Chọn câu trả lời đúng
 Xem đáp án
Xem đáp án
Trả lời:
Áp dụng quy tắc nhân hai số nguyên khác dấu ta có:
\[ - 365.366 < 0 < 1\] nên \[ - 365.366 \ne - 1\]
Đáp án cần chọn là: A
Câu 4:
Chọn câu đúng
 Xem đáp án
Xem đáp án
Trả lời:
Đáp án A: \[( - 20).( - 5) = 100\] nên A sai.
Đáp án B: \[\left( { - 50} \right).\left( { - 12} \right) = 600\] nên B đúng.
Đáp án C:\[( - 18).25 = - 450 \ne - 400\] nên C sai.
Đáp án D: \[11.( - 11) = - 121 \ne - 1111\] nên D sai.
Đáp án cần chọn là: BCâu 5:
Chọn câu sai
 Xem đáp án
Xem đáp án
Trả lời:
Đáp án A: \[( - 19).( - 7) > 0\] đúng vì tích hai số nguyên cùng dấu là một số nguyên dương.
Đáp án B: \[3.\left( { - 121} \right) < 0\] đúng vì tích hai số nguyên khác dấu là một số nguyên âm.
Đáp án C: \[45.( - 11) = - 495 > - 500\] nên C sai.
Đáp án D: \[46.\left( { - 11} \right) = - 506 < - 500\] nên D đúng.
Đáp án cần chọn là: C
Câu 6:
Khi \(x = - 12\) , giá trị của biểu thức \[(x - 8).(x + 7)\] là số nào trong bốn số sau:
 Xem đáp án
Xem đáp án
Trả lời:
Thay \(x = - 12\) vào biểu thức \[(x - 8).(x + 7)\] ta được
\[\begin{array}{l}( - 12 - 8).( - 12 + 7)\\ = ( - 20).( - 5)\\ = 20.5\\ = 100\end{array}\]
Đáp án cần chọn là: B
Câu 7:
 Xem đáp án
Xem đáp án
Trả lời:
Ta có
\[\begin{array}{l}( - 3).( - 3).( - 3).( - 3).( - 3).( - 3).( - 3)\\ = {( - 3)^7} = - {3^7}\end{array}\]
Đáp án cần chọn là: B
Câu 8:
Tính giá trị của biểu thức \[P = {\left( { - 13} \right)^2}.\left( { - 9} \right)\] ta có
 Xem đáp án
Xem đáp án
Trả lời:
\[P = {\left( { - 13} \right)^2}.\left( { - 9} \right) = 169.\left( { - 9} \right) = - 1521\]
Đáp án cần chọn là: D
Câu 9:
Chọn câu đúng
 Xem đáp án
Xem đáp án
Trả lời:
Đáp án A: \[\left( { - 23} \right).\left( { - 16} \right) > 23.\left( { - 16} \right)\] đúng vì \[VT > 0,VP < 0\]
Đáp án B: \[\left( { - 23} \right).\left( { - 16} \right) = 23.\left( { - 16} \right)\] sai vì \[VT > 0,VP < 0\] nên \[VT \ne VP\]
Đáp án C: \[\left( { - 23} \right).\left( { - 16} \right) < 23.\left( { - 16} \right)\] sai vì \[VT > 0,VP < 0\] nên \[VT > VP\]
Đáp án D: \[\left( { - 23} \right).16 > 23.\left( { - 6} \right)\] sai vì:
\[23.\left( { - 6} \right) = - 138\]và \[23.\left( { - 6} \right) = - 138\] mà \[ - 368 < - 138\] nên \[\left( { - 23} \right).16 < 23.\left( { - 6} \right)\]
Đáp án cần chọn là: A
Câu 10:
 Xem đáp án
Xem đáp án
Trả lời:
Thay \[x = 5\] vào PP ta được:
\[\begin{array}{*{20}{l}}{P = \left( {5 - 3} \right).3 - 20.5}\\{ = 2.3 - 100 = 6 - 100 = - 94}\end{array}\]
Đáp án cần chọn là: A
Câu 11:
Cho \[B = \left( { - 8} \right).25.{\left( { - 3} \right)^2}\] và \[C = \left( { - 30} \right).{\left( { - 2} \right)^3}.\left( {{5^3}} \right)\] . Chọn câu đúng
 Xem đáp án
Xem đáp án
Trả lời:
\[B = \left( { - 8} \right).25.{\left( { - 3} \right)^2} = - 200.9 = - 1800\]
\[\begin{array}{*{20}{l}}{C = \left( { - 30} \right).{{\left( { - 2} \right)}^3}.\left( {{5^3}} \right)}\\{ = \left( { - 30} \right).\left( { - 8} \right).125}\\{ = \left( { - 30} \right).\left( { - 1000} \right)}\\{ = 30000}\end{array}\]
Khi đó \[B.50 = - 1800.50 = - 90000;C.( - 3) = 30000.( - 3) = - 90000\]
Vậy \[B.50 = C.( - 3)\]
Đáp án cần chọn là: B
Câu 12:
Có bao nhiêu giá trị x nguyên dương thỏa mãn \[(x - 3).(x + 2) = 0\;\] là:
 Xem đáp án
Xem đáp án
Trả lời:
\[(x - 3).(x + 2) = 0\]
\[\begin{array}{*{20}{l}}{TH1:x - 3 = 0}\\{x = 0 + 3}\\{x = 3\left( {TM} \right)}\end{array}\]
\[\begin{array}{*{20}{l}}{TH2:x + 2 = 0}\\{x = 0 - 2}\\{x = - 2\left( L \right)}\end{array}\]
Vậy có duy nhất 1 giá trị nguyên dương của x thỏa mãn là \[x = 3\]
Đáp án cần chọn là: D
Câu 13:
 Xem đáp án
Xem đáp án
Trả lời:
\[\begin{array}{*{20}{l}}{2\left( {x - 5} \right) - 3\left( {x - 7} \right) = - 2}\\{2x - 10 - 3.x + 3.7 = - 2}\\{2x - 10 - 3x + 21 = - 2}\\{\left( {2x - 3x} \right) + \left( {21 - 10} \right) = - 2}\\{\left( {2 - 3} \right)x + 11 = - 2}\\{ - x + 11 = - 2}\\{ - x = - 2 - 11}\\{ - x = - 13}\\{x = 13}\end{array}\]
Đáp án cần chọn là: A
Câu 14:
Có bao nhiêu giá trị x thỏa mãn \[\left( {x - 6} \right)\left( {{x^2} + 2} \right) = 0\] ?
 Xem đáp án
Xem đáp án
Trả lời:
\[\left( {x - 6} \right)\left( {{x^2} + 2} \right) = 0\]
Vì \[{x^2} \ge 0\] với mọi x nên \[{x^2} + 2 \ge 0 + 2 = 2\] hay \[{x^2} + 2 > 0\] với mọi x
Suy ra
\[\begin{array}{l}x - 6 = 0\\x = 0 + 6\\x = 6\end{array}\]
Vậy chỉ có 1 giá trị của x thỏa mãn là \[x = 6\]
Đáp án cần chọn là: D
Câu 15:
 Xem đáp án
Xem đáp án
Trả lời:
Vì \[\left( { - 4} \right).\left( { - 5} \right) = 4.5 = 20\] nên để \[\left( { - 4} \right).\left( {x - 3} \right) = 20\] thì \[x - 3 = - 5\]
Khi đó ta có:
\[\begin{array}{l}x - 3 = - 5\\x = - 5 + 3\\x = - 2\end{array}\]
Vậy \[x = - 2\]
Đáp án cần chọn là: C
Câu 16:
Số giá trị \[x \in {\rm Z}\;\] để \[\left( {{x^2} - 5} \right)\left( {{x^2} - 25} \right) < 0\] là:
 Xem đáp án
Xem đáp án
Trả lời:
\[\left( {{x^2} - 5} \right)\left( {{x^2} - 25} \right) < 0\] nên \[{x^2} - 5\] và \[{x^2} - 25\] khác dấu
Mà \[{x^2} - 5 > {x^2} - 25\] nên \[{x^2} - 5 > 0\] và \[{x^2} - 25 < 0\]
Suy ra \[{x^2} > 5\] và \[{x^2} < 25\]
Do đó \[{x^2} = 9\] hoặc \[{x^2} = 16\]
Từ đó \[x \in \left\{ { \pm 3; \pm 4} \right\}\]
Vậy có 44 giá trị nguyên của xx thỏa mãn bài toán.
Đáp án cần chọn là: D
Câu 17:
 Xem đáp án
Xem đáp án
Trả lời:
\[\begin{array}{*{20}{l}}{{{\left( {1 - 3x} \right)}^3} = - 8}\\{{{\left( {1 - 3x} \right)}^3} = {{\left( { - 2} \right)}^3}}\\{1 - 3x = - 2}\\{3x = 1 - \left( { - 2} \right)}\\{3x = 3}\\{x = 3:3}\\{x = 1}\end{array}\]
Vậy \[x = 1\]
Đáp án cần chọn là: A
Câu 18:
Số cặp số nguyên (x;y) thỏa mãn \[x.y = - 28\;\] là:
 Xem đáp án
Xem đáp án
Trả lời:
Vì \[ - 28 = - 1.28 = 1.\left( { - 28} \right) = - 2.14 = 2.\left( { - 14} \right) = - 4.7 = 4.( - 7)\]
Nên ta có các bộ (x;y) thỏa mãn bài toán là:
\[\begin{array}{l}\left( { - 1;28} \right),\left( {28; - 1} \right),\left( {1; - 28} \right),\left( { - 28;1} \right),\left( { - 2;14} \right),\left( {14; - 2} \right),\\(2; - 14),( - 14;2),\left( { - 4;7} \right),\left( {7; - 4} \right),(4; - 7),( - 7;4).\end{array}\]
Có tất cả 12 bộ số (x;y) thỏa mãn bài toán.
Đáp án cần chọn là: D
Câu 19:
Giá trị nhỏ nhất của biểu thức \[3{(x + 1)^2} + 7\] là
 Xem đáp án
Xem đáp án
Trả lời:
Ta có:
\[{\left( {x + 1} \right)^2} \ge 0\] với mọi x
\[ \Rightarrow 3.{\left( {x + 1} \right)^2} \ge 0\] với mọi x
\[\begin{array}{l} \Rightarrow 3{\left( {x + 1} \right)^2} + 7 \ge 0 + 7\\ \Rightarrow 3{\left( {x + 1} \right)^2} + 7 \ge 7\end{array}\]
Vậy GTNN của biểu thức là 7 đạt được khi \[x = - 1.\] .
Đáp án cần chọn là: B
Câu 20:
Có bao nhiêu cặp số \[x;y \in Z\;\] thỏa mãn \[xy + 3x - 7y = 23\] ?
 Xem đáp án
Xem đáp án
Trả lời:
\[\begin{array}{l}xy + 3x - 7y - 23 = 0\\xy + 3x - 7y - 21 - 2 = 0\\x(y + 3) - 7(y + 3) = 2\\(x - 7)(y + 3) = 2\end{array}\]
Ta có các trường hợp:

Vậy các cặp số (x,y) là \[\left\{ {\left( {8; - 1} \right);\left( {9; - 2} \right);\left( {6; - 5} \right);\left( { - 5; - 4} \right)} \right\}\]
Vậy có 4 cặp số thỏa mãn bài toán.
Đáp án cần chọn là: D
Câu 21:
Ba bạn An, Bình, Cường chơi ném tiêu với bia gồm năm vòng như hình 3.19. Kết quả được ghi lại trong bảng sau:
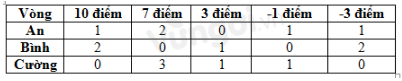
Sắp xếp tên các bạn theo thứ tự từ thấp đến cao là?
 Xem đáp án
Xem đáp án
Trả lời:
Số điểm của An là: \[10.1{\rm{ }} + {\rm{ }}2.7{\rm{ }} + {\rm{ }}1.\left( { - 1} \right){\rm{ }} + {\rm{ }}1.\left( { - 3} \right){\rm{ }} = {\rm{ }}20\]
Số điểm của Bình là: \[2.10{\rm{ }} + {\rm{ }}1.3{\rm{ }} + {\rm{ }}2.\left( { - 3} \right){\rm{ }} = {\rm{ }}17\]
Số điểm của Cường là: \[3.7{\rm{ }} + {\rm{ }}1.3{\rm{ }} + {\rm{ }}1.\left( { - 1} \right){\rm{ }} = {\rm{ }}23\]
Sắp xếp tên các bạn theo thứ tự từ thấp đến cao: Bình, An, Cường.
Đáp án cần chọn là: B
Câu 22:
Công ty Ánh Dương có lợi nhuận ở mỗi tháng trong Quý I là – 30 triệu đồng. Trong Quý II, lợi nhuận mỗi tháng của công ty là 70 triệu đồng. Sau 6 tháng đầu năm, lợi nhuận của công ty Ánh Dương là?
 Xem đáp án
Xem đáp án
Trả lời:
* Lợi nhuận Quý I là \[( - 30).3 = - 90\] triệu đồng.
* Lợi nhuận Quý II là \[70.3 = 210\] triệu đồng.
Sau 6 tháng đầu năm, lợi nhuận của công ty Ánh Dương là: \[( - 90) + 210 = 120\] triệu đồng.
Đáp án cần chọn là: A
Câu 23:
Có bao nhiêu số nguyên xx thỏa mãn \[(x - 7)(x + 5) < 0\] ?
 Xem đáp án
Xem đáp án
Trả lời:
\[\left( {x - 7} \right)\left( {x + 5} \right) < 0\] nên \[x - 7\] và \[x + 5\] khác dấu
Mà \[x + 5 > x - 7\] nên \[x + 5 > 0\] và \(x - 7 < 0\)
Suy ra \(x > - 5\) và \(x < 7\)
Do đó \[x \in \left\{ { - 4, - 3, - 2, - 1,0,1,2,3,4,5,6} \right\}\]
Vậy có 11 giá trị nguyên của x thỏa mãn bài toán.
Đáp án cần chọn là: B
Câu 24:
+) Tích của một số chẵn các số nguyên âm là một số nguyên ..(1)..
+) Tích của một số lẻ các số nguyên âm là một số nguyên ..(2)..
Từ thích hợp để điền vào hai chỗ chấm trên lần lượt là:
 Xem đáp án
Xem đáp án
Trả lời:
+) Tích của một số chẵn các số nguyên âm là một số nguyên dương
+) Tích của một số lẻ các số nguyên âm là một số nguyên âm
Đáp án cần chọn là: B
