Trắc nghiệm Toán 6 KNTT Mở rộng phân số. Phân số bằng nhau có đáp án (Phần 2)
Trắc nghiệm Toán 6 KNTT Bài 2. Các dạng toán về mở rộng khái niệm phân số, phân số bằng nhau có đáp án
-
321 lượt thi
-
16 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Hãy viết phép chia sau dưới dạng phân số: (- 58) : 73
Xem đáp án
Trả lời:
Phép chia (−58):73 được viết dưới dạng phân số là \[\frac{{ - 58}}{{73}}\]
Đáp án cần chọn là: ACâu 2:
Phần tô màu trong hình sau biểu diễn phân số nào?
Xem đáp án
Trả lời:
Trong hình có 2 ô vuông tô màu và tổng tất cả 8 ô vuông nên phân số biểu thị là \[\frac{2}{8} = \frac{1}{4}\]
Đáp án cần chọn là: B
Câu 3:
Chọn câu sai?
Xem đáp án
Trả lời:
Đáp án A: Vì \[1.135 = 3.45\] nên \[\frac{1}{3} = \frac{{45}}{{135}}\]
→ A đúng
Đáp án B: Vì \[\left( { - 13} \right).\left( { - 40} \right) = 20.26\] nên \[\frac{{ - 13}}{{20}} = \frac{{26}}{{ - 40}}\]
→ B đúng
Đáp án C: Vì \[\left( { - 4} \right).\left( { - 60} \right) \ne 15.\left( { - 16} \right)\] nên \[\frac{{ - 4}}{{15}} = \frac{{ - 16}}{{ - 60}}\]
→ C sai
Đáp án D: Vì \[6.\left( { - 49} \right) = 7.\left( { - 42} \right)\] nên \[\frac{6}{7} = \frac{{ - 42}}{{ - 49}}\]
→ D đúng
Đáp án cần chọn là: C
Câu 4:
Tìm số nguyên x biết \[\frac{{35}}{{15}} = \frac{x}{3}\]
Xem đáp án
Trả lời:
\[\frac{{35}}{{15}} = \frac{x}{3}\]
\[35.3 = 15.x\]
\[x = \frac{{35.3}}{{15}}\]
\[x = 7\]
Vậy x = 7
Đáp án cần chọn là: A
Câu 5:
Viết 20 dm2 dưới dạng phân số với đơn vị là mét vuông
Xem đáp án
Trả lời:
Ta có: \[20d{m^2} = \frac{{20}}{{100}}\left( {{m^2}} \right)\]
Đáp án cần chọn là: B
Câu 6:
Cho biểu thức \[C = \frac{{11}}{{2n + 1}}\]. Tìm tất cả các giá trị của n nguyên để giá trị của C là một số tự nhiên.
Xem đáp án
Trả lời:
Vì C ∈ N nên C ∈ Z. Do đó ta tìm n ∈ Z để C ∈ Z
Vì n ∈ Z nên để C ∈ Z thì 2n + 1 ∈ U(11) = {±1 ;±11}
Ta có bảng:
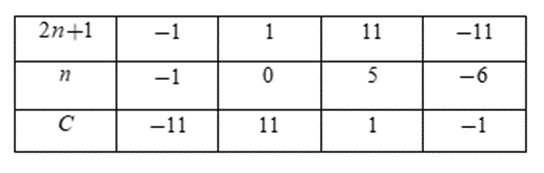
Vì C ∈ N nên ta chỉ nhận các giá trị n = 0; n = 5
Đáp án cần chọn là: C
Câu 7:
Có bao nhiêu giá trị nguyên dương của n để \[\frac{9}{{4n + 1}}\] đạt giá trị nguyên.
Xem đáp án
Trả lời:
Vì n nguyên dương nên để \[\frac{9}{{4n + 1}}\]nguyên thì 4n + 1 ∈ U(9) = {±1; ±3; ±9}
Ta có bảng:
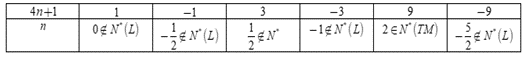
Vậy có duy nhất một giá trị của nn thỏa mãn là n=2
Đáp án cần chọn là: A
Câu 8:
Cho các phân số: \[\frac{{15}}{{60}};\frac{{ - 7}}{5};\frac{6}{{15}};\frac{{28}}{{ - 20}};\frac{3}{{12}}\]
Số cặp phân số bằng nhau trong những phân số trên là:
Xem đáp án
Trả lời:
- Các phân số dương: \[\frac{{15}}{{60}};\frac{6}{{15}};\frac{3}{{12}}\]
+ Vì: \[15.15 \ne 60.6\] Nên \[\frac{{15}}{{60}} \ne \frac{6}{{15}}\]
+ Vì: \[6.12 \ne 15.3\] Nên \[\frac{6}{{15}} \ne \frac{3}{{12}}\]
+ Vì: \[15.12 = 60.3\] Nên \[\frac{{15}}{{60}} = \frac{3}{{12}}\]
- Các phân số âm: \[\frac{{ - 7}}{5};\frac{{28}}{{ - 20}}\]
Vì \[\left( { - 7} \right).\left( { - 20} \right) = 5.28\]
Nên \[\frac{{ - 7}}{5} = \frac{{28}}{{ - 20}}\]
Vậy có hai cặp phân số bằng nhau trong các phân số đã cho.
Đáp án cần chọn là: D
Câu 9:
Tính tổng các giá trị \[x \in Z\]biết rằng \[ - \frac{{111}}{{37}} < x < \frac{{91}}{{13}}\]
Xem đáp án
Trả lời:
Ta có:
\[ - \frac{{111}}{{37}} < x < \frac{{91}}{{13}}\]
\[ \Rightarrow - 3 < x < 7\]
\[ \Rightarrow x \in \left\{ { - 2; - 1;0;1;2;3;4;5;6} \right\}\]
Vậy tổng các giá trị của x thỏa mãn là: (−2) + (−1) + ... + 5 + 6 = 18
Đáp án cần chọn là: C
Câu 10:
Tìm tập hợp các số nguyên n để \[A = \frac{{3n - 5}}{{n + 4}}\] có giá trị là số nguyên.
Xem đáp án
Trả lời:
Ta có:
\[A = \frac{{3n - 5}}{{n + 4}} = \frac{{3n + 12 - 12 - 5}}{{n + 4}} = \frac{{3\left( {n + 4} \right) + \left( { - 17} \right)}}{{n + 4}}\]
\[ = \frac{{3\left( {n + 4} \right)}}{{n + 4}} + \frac{{ - 17}}{{n + 4}} = 3 + \frac{{ - 17}}{{n + 4}}\]
Vì \[n \in Z\]nên để \[A \in Z\] thì \[n + 4 \in U\left( { - 17} \right) = \left\{ { \pm 1; \pm 17} \right\}\]
Ta có bảng:
Vậy \[n \in \left\{ { - 21; - 5; - 3;13} \right\}\]
Đáp án cần chọn là: B
Câu 11:
Có bao nhiêu cặp số nguyên (x; y) thỏa mãn \[\frac{x}{5} = \frac{3}{y}\] và x > y
Xem đáp án
Ta có:
\[\frac{x}{5} = \frac{3}{y} \Rightarrow x.y = 5.3 = 15\]
Mà \[15 = 5.3 = 15.1 = \left( { - 3} \right).\left( { - 5} \right) = \left( { - 1} \right).\left( { - 15} \right)\]
Và \[x,y \in Z,x < y\]
Nên \[\left( {x;y} \right) \in \left\{ {\left( {5;3} \right),\left( {15;1} \right),\left( { - 3; - 5} \right),\left( { - 1; - 15} \right)} \right\}\]
Đáp án cần chọn là: A
Câu 12:
Tìm x; y biết \[\frac{{x - 4}}{{y - 3}} = \frac{4}{3}\] và x – y = 5
Xem đáp án
Trả lời:
Ta có:
\[x - y = 5 \Rightarrow x = y + 5\]
Thay vào \[\frac{{x - 4}}{{y - 3}} = \frac{4}{3}\]
ta được:
\[\frac{{y + 5 - 4}}{{y - 3}} = \frac{4}{3}\]
\[\frac{{y + 1}}{{y - 3}} = \frac{4}{3}\]
\[3\left( {y + 1} \right) = 4\left( {y - 3} \right)\]
\[3y + 3 = 4y - 12\]
\[3y - 4y = - 12 - 3\]
\[ - y = - 15\]
\[ \Rightarrow x = 15 + 5 = 20\]
Vậy x = 20; y = 15
Đáp án cần chọn là: C
Câu 13:
Tìm số nguyên x biết rằng \[\frac{x}{3} = \frac{{27}}{x}\] và x < 0.
Xem đáp án
Trả lời:
\[\frac{x}{3} = \frac{{27}}{x}\]
x.x = 81
x2 = 81
Ta có: x = 9 hoặc x = −9
Kết hợp điều kiện x < 0 nên có một giá trị x thỏa mãn là: x = −9
Đáp án cần chọn là: C
Câu 14:
Viết số nguyên a dưới dạng phân số ta được:
Xem đáp án
Trả lời:
Viết số nguyên a dưới dạng phân số ta được: \[\frac{a}{1}\]
Đáp án cần chọn là: C
Câu 15:
Cách viết nào sau đây cho ta một phân số:
Xem đáp án
Trả lời:
+ \[\frac{4}{0}\] có mẫu bằng 0 nên không là phân số
+ \[\frac{{1,5}}{3}\]có \[1,5 \notin Z\]nên không là phân số
+ \[\frac{0}{7}\] là phân số
+ \[\frac{{ - 5}}{{3,5}}\]có \[3,5 \notin Z\]nên không là phân số
Đáp án cần chọn là: C
Câu 16:
Phân số \[\frac{{ - 9}}{7}\]được đọc là:
Xem đáp án
Trả lời:
Phân số \[\frac{{ - 9}}{7}\]được đọc là: Âm chín phần bảy
Đáp án cần chọn là: D