52 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 6 CD Bài 1: Phân số với tử và mẫu là số nguyên có đáp án

Câu 1:

Viết phân số năm phần tám

A.

\frac{5}{8}

B.

\frac{8}{- 5}

C.

\frac{- 5}{8}

D. – 5,8

Xem đáp án

Phân số âm năm phần tám được viết là $\frac{- 5}{8}$

Đáp án cần chọn là: C

Câu 2:

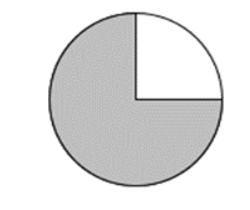
Phần tô màu trong hình sau biểu diễn phân số nào?

A.

\frac{1}{2}

B.

\frac{1}{4}

C.

\frac{3}{4}

D.

\frac{5}{8}

Xem đáp án

Quan sát hình vẽ ta thấy nếu chia hình tròn làm 4 phần thì phần tô màu chiếm 3 phần.

Vậy phân số biểu diễn phần tô màu là $\frac{3}{4}$

Đáp án cần chọn là: C

Câu 3:

Hãy viết phép chia sau dưới dạng phân số: (-58) : 73

A.

\frac{- 58}{73}

B.

\frac{58}{73}

C.

\frac{73}{- 58}

D.

\frac{- 73}{58}

Xem đáp án

Phép chia (-58) : 73 được viết dưới dạng phân số là $\frac{- 58}{73}$

Đáp án cần chọn là: A

Câu 4:

Phân số nào dưới đây bằng với phân số $\frac{- 2}{5}$

A.

\frac{4}{10}

B.

\frac{- 6}{15}

C.

\frac{6}{15}

D.

\frac{- 4}{10}

Xem đáp án

Đáp án A: Vì −2.10 ≠ 4.5nên $\frac{- 2}{5} \neq \frac{4}{10}$

⇒ A sai.

Đáp án B: Vì (−2).15 = (−6).5=−30 nên −25 = −615

⇒ B đúng.

Đáp án C: (−2).15 ≠ 6.5 nên −25 ≠ 615

⇒ C sai.

Đáp án D: Vì (−2).(−10) ≠ (−4).5 nên −25 ≠ −4 − 10

⇒ D sai.

Đáp án cần chọn là: B

Câu 5:

Tìm số nguyên x biết $\frac{35}{15} = \frac{x}{3}$

A. x = 7

B. x = 5

C. x = 15

D. x = 6

Xem đáp án

$\frac{35}{15} = \frac{x}{3}$

35.3 = 15.x

$x = \frac{35.3}{15}$

x = 7

Vậy x = 7

Đáp án cần chọn là: A

Câu 6:

Cho tập A={1; −2; 3; 4}. Có bao nhiêu phân số có tử số và mẫu số thuộc A mà có tử số khác mẫu số và tử số trái dấu với mẫu số?

A. 9

B. 6

C. 3

D. 12

Xem đáp án

Các phân số thỏa mãn bài toán là:

$\frac{1}{- 2}; \frac{3}{- 2}; \frac{4}{- 2}; \frac{- 2}{1}; \frac{- 2}{3}; \frac{- 2}{4}$

Vậy có tất cả 6 phân số.

Đáp án cần chọn là: B

Câu 7:

Viết 20 dm² dưới dạng phân số với đơn vị là mét vuông

A.

\frac{100}{20} (m^{2})

B. $\frac{20}{100} (m^{2})$

C.

\frac{20}{10} (m^{2})

D.

\frac{20}{1000} (m^{2})

Xem đáp án

Ta có: $20 d m^{2} = \frac{20}{100} (m^{2})$

Đáp án cần chọn là: B

Câu 8:

Nhận xét nào sau đây là đúng khi nói về phân số?

A. Phân số nhỏ hơn số 0 gọi là phân số âm.

B. Phân số lớn hơn số 0 gọi là phân số dương.

C. Phân số âm nhỏ hơn phân số dương.

D. Cả A, B và C đều đúng.

Xem đáp án

Những nhận xét đúng là:

- Phân số nhỏ hơn số 0 gọi là phân số âm.

- Phân số lớn hơn số 0 gọi là phân số dương.

- Phân số âm nhỏ hơn phân số dương.

Đáp án cần chọn là: D

Câu 9:

Tìm số nguyên x biết rằng $\frac{x}{3} = \frac{27}{x}$ và x < 0.

A. x = 81

B. x = −81

C. x = −9

D. x = 9

Xem đáp án

$\frac{x}{3} = \frac{27}{x}$

x.x = 81

x² = 81

Ta có: x = 9 hoặc x = −9

Kết hợp điều kiện x < 0 nên có một giá trị x thỏa mãn là: x = −9

Đáp án cần chọn là: C

Câu 10:

Viết số nguyên a dướu dạng phân số ta được:

A.

\frac{a}{0}

B.

\frac{0}{a}

C.

\frac{a}{1}

D.

\frac{1}{a}

Xem đáp án

Viết số nguyên aa dưới dạng phân số ta được: $\frac{a}{1}$

Đáp án cần chọn là: C

Câu 11:

Phân số $\frac{- 9}{7}$ được đọc là:

A. Chín phần bảy

B. Âm bảy phần chín

C. Bảy phần chín

D. Âm chín phần bảy

Xem đáp án

Phân số $\frac{- 9}{7}$ được đọc là: Âm chín phần bảy

Đáp án cần chọn là: D

Câu 12:

Phân số có tử bằng – 4; mẫu bằng 5 được viết là:

A.

\frac{- 5}{4}

B.

\frac{4}{5}

C.

\frac{- 4}{5}

D.

\frac{5}{4}

Xem đáp án

Phân số có tử bằng −4, mẫu bằng 5 được viết là: $\frac{- 4}{5}$

Đáp án cần chọn là: C

Câu 13:

Trong các cách viết sau đây, cách viết nào cho ta phân số:

A.

\frac{12}{0}

B. $\frac{- 4}{5}$

C.

\frac{3}{0, 25}

D.

\frac{4, 4}{11, 5}

Xem đáp án

+) $\frac{12}{0}$ không là phân số vì mẫu số bằng 0.

+) $\frac{3}{0, 25}$ không là phân số vì mẫu số là số thập phân.

+) $\frac{4, 4}{11, 5}$ không là phân số vì tử số và mẫu số là số thập phân.

+) $\frac{- 4}{5}$ là phân số vì −4;5∈Z và mẫu số là 5 khác 0.

Đáp án cần chọn là: B

Câu 14:

Phần tô màu trong hình sau biểu diễn phân số nào?

A.

\frac{1}{2}

B.

\frac{1}{4}

C.

\frac{3}{4}

D.

\frac{5}{8}

Xem đáp án

Trong hình có 2 ô vuông tô màu và tổng tất cả 8 ô vuông nên phân số biểu thị là $\frac{2}{8} = \frac{1}{4}$

Đáp án cần chọn là: B

Câu 15:

Chọn câu sai?

A.

\frac{1}{3} = \frac{45}{135}

B.

\frac{- 13}{20} = \frac{26}{- 40}

C.

\frac{- 4}{15} = \frac{- 16}{- 60}

D.

\frac{6}{7} = \frac{- 42}{- 49}

Xem đáp án

Đáp án A: Vì 1.135 = 3.45 nên $\frac{1}{3} = \frac{45}{135}$

⇒A đúng.

Đáp án B: Vì (−13).(−40) = 20.26 nên $\frac{- 13}{20} = \frac{26}{- 40}$

⇒B đúng.

Đáp án C: Vì (−4).(−60) ≠ 15.(−16) nên $\frac{- 4}{15} \neq \frac{- 16}{- 60}$

⇒C sai.

Đáp án D: Vì 6.(−49) = 7.(−42) nên $\frac{6}{7} = \frac{- 42}{- 49}$

⇒D đúng.

Đáp án cần chọn là: C

Câu 16:

Điền số thích hợp vào chỗ chấm $\frac{15}{90} = \frac{5}{....}$

A. 20

B. -60

C. 60

D. 30

Xem đáp án

$\frac{15}{90} = \frac{5}{x}$

15.x = 90.5

$x = \frac{90.5}{15}$

x = 30

Vậy số cần điền là: 30

Đáp án cần chọn là: D

Câu 17:

Cho biểu thức $C = \frac{11}{2 n + 1}$ . Tìm tất cả các giá trị của n nguyên để giá trị của C là một số tự nhiên.

A.

n \in \{- 6; - 1; 0; 5\}

B.

n \in \{- 1; 5\}

C.

n \in \{0; 5\}

D.

n \in \{1; 11\}

Xem đáp án

Vì $C \in N \Rightarrow C \in Z$ . Do đó ta tìm $n \in Z$ để $C \in Z$

Vì $n \in Z$ nên để $C \in Z$ thì $2 n + 1 \in U (11) = \{\pm 1; \pm 11\}$

Ta có bảng:

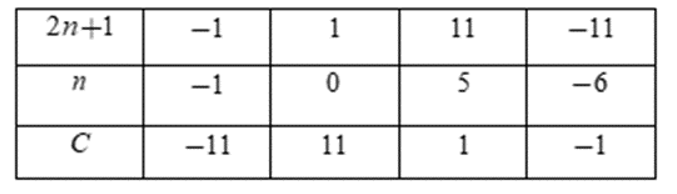
Cho biểu thức C= 11/ 2n+1. Tìm tất cả các giá trị của n nguyên để giá trị của C là một số tự nhiên. (ảnh 1)

Vì $C \in Z$ nên ta chỉ nhận các giá trị n = 0; n = 5

Đáp án cần chọn là: C

Câu 18:

Có bao nhiêu giá trị nguyên dương của n để $\frac{9}{4 n + 1}$ đạt giá trị nguyên.

A. 1

B. 0

C. 2

D. 3

Xem đáp án

Vì n nguyên dương nên để $\frac{9}{4 n + 1}$ nguyên thì 4n+1∈U(9) = {±1; ±3; ±9}

Ta có bảng:

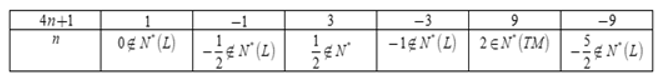
Có bao nhiêu giá trị nguyên dương của n để 9/4n+1 đạt giá trị nguyên. (ảnh 1)

Vậy có duy nhất một giá trị của nn thỏa mãn là n = 2

Đáp án cần chọn là: A

Câu 19:

Tổng các số a, b, c thỏa mãn $\frac{6}{9} = \frac{12}{a} = \frac{b}{- 54} = \frac{- 738}{c}$ là:

A. 1161

B. – 1125

C. – 1053

D. 1089

Xem đáp án

Ta có: $\frac{6}{9} = \frac{12}{a} \Rightarrow 6. a = 9.12 \Rightarrow a = \frac{9.12}{6} = 18$

$\frac{6}{9} = \frac{b}{- 54} \Rightarrow 6. (- 54) = 9. b \Rightarrow b = \frac{6. (- 54)}{9} = - 36$

$\frac{6}{9} = \frac{- 738}{c} \Rightarrow 6. c = 9. (- 738) \Rightarrow c = \frac{9. (- 738)}{6} = - 1107$

Vậy a + b + c = 18 + (−36) + (−1107) = −1125

Đáp án cần chọn là: B

Câu 20:

Cho các phân số: $\frac{15}{60}; \frac{- 7}{5}; \frac{6}{15}; \frac{28}{- 20}; \frac{3}{12}$

Số cặp phân số bằng nhau trong những phân số trên là:

A. 4

B. 2

C. 3

D. 2

Xem đáp án

- Các phân số dương: $\frac{15}{60}; \frac{6}{15}; \frac{3}{12}$

+ Vì 15.15 ≠ 60.6 nên $\frac{15}{60} \neq \frac{6}{15}$

+ Vì 6.12 ≠ 15.3 nên $\frac{6}{15} \neq \frac{3}{12}$

+ Vì 15.12 = 60.3 nên $\frac{15}{60} \neq \frac{3}{12}$

- Các phân số âm: $\frac{- 7}{5}; \frac{28}{- 20}$

Vì (−7).(−20) = 5.28 nên $\frac{- 7}{5} = \frac{28}{- 20}$

Vậy có hai cặp phân số bằng nhau trong các phân số đã cho.

Đáp án cần chọn là: D

Câu 21:

Tính tổng các giá trị x∈Z biết rằng $- \frac{111}{37} < x < \frac{91}{13}$

A. 2

B. 20

C. 18

D. 15

Xem đáp án

Ta có:

$- \frac{111}{37} < x < \frac{91}{13}$ ⇒−3<x<7

⇒ x ∈ {−2; −1; 0; 1; 2; 3; 4; 5; 6}

Vậy tổng các giá trị của x thỏa mãn là: (−2) + (−1) +...+ 5 + 6 = 18

Đáp án cần chọn là: C

Câu 22:

Tìm tập hợp các số nguyên nn để $A = \frac{3 n - 5}{n + 4}$ có giá trị là số nguyên.

A. n∈{13}

B. n∈{−21; −5; −3; 13}

C. n∈{−17; −1; 1; 17}

D. n∈{−13; −3; 3; 13}

Xem đáp án

Ta có:

$A = \frac{3 n - 5}{n + 4} = \frac{3 n + 12 - 12 - 5}{n + 4} = \frac{3 (n + 4) + (- 17)}{n + 4}$

$= \frac{3 (n + 4)}{n + 4} + \frac{- 17}{n + 4} = 3 + \frac{- 17}{n + 4}$

Vì $n \in Z$ nên để $A \in Z$ thì $n + 4 \in U (- 17) = \{\pm 1; \pm 17\}$

Ta có bảng:

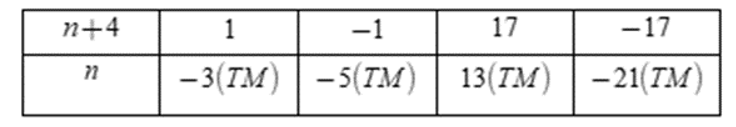
Tìm tập hợp các số nguyên nn để A= 3n-5/ n+4 có giá trị là số nguyên. (ảnh 1)

Vậy $n \in \{- 21; - 5; - 3; 13\}$

Đáp án cần chọn là: B

Câu 23:

Có bao nhiêu cặp số nguyên (x; y) thỏa mãn $\frac{x}{5} = \frac{3}{y}$ và x > y?

A. 4

B. 3

C. 2

D. 1

Xem đáp án

Ta có: $\frac{x}{5} = \frac{3}{y}$ ⇒ x.y = 5.3 = 15

Mà 15 = 5.3 = 15.1 = (−3).(−5) = (−1).(−15)

và x,y∈Z, x > y nên (x;y)∈{(5; 3), (15; 1), (−3; −5), (−1; −15)}

Đáp án cần chọn là: A

Câu 24:

Tìm x; y biết $\frac{x - 4}{y - 3} = \frac{4}{3}$ và x – y = 5.

A. x = 15; y = 5

B. x = 5; y = 15

C. x = 20; y = 15

D. x = 25; y = 10

Xem đáp án

Ta có:

Xx – y = 5 ⇒ x = y + 5 thay vào $\frac{x - 4}{y - 3} = \frac{4}{3}$ ta được:

$\frac{y + 5 - 4}{y - 3} = \frac{4}{3}$

$\frac{y + 1}{y - 3} = \frac{4}{3}$

3(y + 1) = 4(y − 3)

3y + 3 = 4y − 12

3y − 4y = −12 − 3

−y = −15

y = 15

⇒ x = 15 + 5 = 20

Vậy x = 20; y = 15

Đáp án cần chọn là: C

Câu 25:

Viết số nguyên −16 dưới dạng phân số ta được:

A.

\frac{- 16}{0}

B.

\frac{16}{1}

C.

\frac{- 16}{0}

D.

\frac{16}{0}

Xem đáp án

Viết số nguyên −16 dưới dạng phân số ta được: $\frac{- 16}{1}$

Đáp án cần chọn là: C

Câu 26:

Cách viết nào sau đây cho ta một phân số:

A. $\frac{4}{0}$

B. $\frac{1, 5}{3}$

C. $\frac{0}{7}$

D. $\frac{- 5}{3, 5}$

Xem đáp án

+ $\frac{4}{0}$ có mẫu bằng 0 nên không là phân số

+ $\frac{1, 5}{3}$ có 1,5∉Z nên không là phân số

+ $\frac{0}{7}$ là phân số

+ $\frac{- 5}{3, 5}$ có 3,5∉Z nên không là phân số

Chọn đáp án C

Câu 27:

Chọn câu sai. Với $a, b, m \in Z; b, m \neq 0$ thì:

A.

\frac{a}{b} = \frac{a . m}{b . m}

B.

\frac{a}{b} = \frac{a + m}{b + m}

C.

\frac{a}{b} = \frac{- a}{- b}

D.

\frac{a}{b} = \frac{a : n}{b : n}

với n là ước chung của a, b.

Xem đáp án

Dựa vào các tính chất cơ bản của phân số:

$\frac{a}{b} = \frac{a . m}{b . m}$ với $m \in Z$ và $m \neq 0; \frac{a}{b} = \frac{a : n}{b : n}$ với $n \in U C (a; b)$ và $\frac{a}{b} = \frac{- a}{- b}$ thì các đáp án A, C, D đều đúng.

Đáp án B sai.

Đáp án cần chọn là: B

Câu 28:

Phân số $\frac{a}{b}$ là phân số tối giản khi ƯC(a; b) bằng

A. {1; −1}

B. {2}

C. {1; 2}

D. {1; 2; 3}

Xem đáp án

Phân số tối giản (hay phân số không rút gọn được nữa) là phân số mà cả tử và mẫu chỉ có ước chung là 1 và −1.

Đáp án cần chọn là: A

Câu 29:

Tìm số a; b biết $\frac{24}{56} = \frac{a}{7} = \frac{- 111}{b}$

A. a = 3, b = −259

B. a = −3, b = −259

C. a = 3, b = 259

D. a = −3, b = 259

Xem đáp án

Ta có:

$\frac{24}{56} = \frac{24 : 8}{56 : 8} = \frac{3}{7} = \frac{a}{7} \Rightarrow a = 3$

$\frac{3}{7} = \frac{3. (- 37)}{7. (- 37)} = \frac{- 111}{- 259} = \frac{- 111}{b} \Rightarrow b = - 259$

Vậy a = 3, b = −259

Đáp án cần chọn là: A.

Câu 30:

Phân số nào dưới đây là phân số tối giản?

A.

\frac{- 2}{4}

B.

\frac{- 15}{- 96}

C.

\frac{13}{27}

D.

\frac{- 29}{58}

Xem đáp án

Đáp án A: ƯCLN(2; 4) = 2 ≠ 1 nên loại.

Đáp án B: ƯCLN(15; 96) = 3 ≠ 1 nên loại.

Đáp án C: ƯCLN(13; 27) = 1 nên C đúng.

Đáp án D: ƯCLN(29; 58) = 29 ≠ 1nên D sai.

Đáp án cần chọn là: C

Câu 31:

Rút gọn phân số $\frac{600}{800}$ về dạng phân số tối giản ta được:

A.

\frac{1}{2}

B.

\frac{6}{8}

C.

\frac{3}{4}

D.

\frac{- 3}{4}

Xem đáp án

Ta có: UwCLN (600, 800) = 200

$\frac{600}{800} = \frac{600 : 200}{800 : 200} = \frac{3}{4}$

Đáp án cần chọn là: C

Câu 32:

Rút gọn phân số $\frac{(- 2) .3 + 6.5}{9.6}$ về dạng phân số tối giản ta được phân số có tử số là:

A.

\frac{4}{9}

B. 31

C. – 1

D. 4

Xem đáp án

Ta có:

$\frac{(- 2) .3 + 6.5}{9.6} = \frac{- 6 + 30}{54} = \frac{24}{54} = \frac{24 : 6}{54 : 6} = \frac{4}{9}$

Vậy tử số của phân số cần tìm là 4

Đáp án cần chọn là: D

Câu 33:

Tìm x biết $\frac{2323}{3232} = \frac{x}{32}$

A. 101

B. 32

C. – 32

D. 23

Xem đáp án

Ta có: $\frac{2323}{3232} = \frac{2323 : 101}{3232 : 101} = \frac{23}{32} = \frac{x}{32} \Rightarrow x = 23$

Đáp án cần chọn là: D

Câu 34:

Rút gọn phân số $\frac{4.8}{64. (- 7)}$ ta được phân số tối giản là:

A.

\frac{- 1}{7}

B.

\frac{- 1}{14}

C.

\frac{4}{- 56}

D.

\frac{- 1}{70}

Xem đáp án

Ta có: $\frac{4.8}{64. (- 7)} = \frac{4.8}{2.4.8. (- 7)} = \frac{1}{2. (- 7)} = \frac{- 1}{14}$

Đáp án cần chọn là: B

Câu 35:

Rút gọn biểu thức $A = \frac{3. (- 4) .60 - 60}{50.20}$ ta được:

A.

\frac{- 13}{25}

B.

\frac{- 18}{25}

C.

\frac{- 6}{25}

D.

\frac{- 39}{50}

Xem đáp án

Ta có:

$A = \frac{3. (- 4) .60 - 60}{50.20} = \frac{[3. (- 4) - 1] .60}{50.20}$

$= \frac{- 13.60}{50.20} = \frac{- 13.3}{50} = \frac{- 39}{50}$

Đáp án cẩn chọn là: D

Câu 36:

Phân số nào sau đây là kết quả của biểu thức $\frac{2.9.52}{22. (- 72)}$ sau khi rút gọn đến tối giản?

A.

\frac{- 13}{22}

B.

\frac{13}{22}

C.

\frac{- 13}{18}

D.

\frac{- 117}{198}

Xem đáp án

$\frac{2.9.52}{22. (- 72)} = \frac{{2.3}^{2} {.2}^{2} .13}{2.11. (- 2^{3} {.3}^{2})}$

$= \frac{2^{3} {.3}^{2} .13}{- 2^{4} {.3}^{2} .11} = \frac{13}{- 2.11} = \frac{- 13}{22}$

Đáp án cần chọn là: A

Câu 37:

Rút gọn phân số $\frac{- 12 a}{24}, a \in Z$ ta được:

A.

\frac{a}{2}

B.

\frac{1}{2}

C.

\frac{- 1}{2}

D.

\frac{- a}{2}

Xem đáp án

Ta có:

$\frac{- 12 a}{24} = \frac{(- 1) .12. a}{12.2} = \frac{(- 1) . a}{2} = \frac{- a}{2}$

Đáp án cần chọn là: D

Câu 38:

Phân số $\frac{- m}{- n}; n, m \in Z; n \neq 0$ bằng phân số nào sau đây?

A. $\frac{m}{n}$

B.

\frac{n}{m}

C. $\frac{- n}{m}$

D.

\frac{- m}{n}

Xem đáp án

Ta có: $\frac{- m}{- n} = \frac{m}{n}$

Đáp án cần chọn là: A

Câu 39:

Quy đồng mẫu số hai phân số $\frac{2}{7}; \frac{5}{- 8}$ được hai phân số lần lượt là:

A.

\frac{16}{56}; \frac{- 35}{56}

B.

\frac{16}{56}; \frac{35}{56}

C.

\frac{16}{56}; \frac{35}{- 56}

D.

\frac{- 16}{56}; \frac{- 35}{56}

Xem đáp án

Ta quy đồng $\frac{2}{7}$ và $\frac{5}{- 8}$ (MSC: 56)

$\frac{2}{7} = \frac{2.8}{7.8} = \frac{16}{56}$ ; $\frac{- 5}{8} = \frac{- 5.7}{8.7} = \frac{- 35}{56}$

Đáp án cần chọn là: A

Câu 40:

Mẫu số chung của các phân số $\frac{2}{5}; \frac{23}{18}; \frac{5}{75}$ là:

A. 180

B. 500

C. 750

D. 450

A. 180

B. 500

C. 750

D. 450

Xem đáp án

Ta có:

5 = 5.1

18 = 2.3²

75 = 3.5²

⇒BCNN(5; 18; 75) = 2.3².5²= 450

Vậy ta có thể chọn một mẫu chung là 450

Đáp án cần chọn là: D

Câu 41:

Mẫu chung nguyên dương nhỏ nhất của các phân số $\frac{19}{3^{2} .7.11}; \frac{23}{3^{2} {.7}^{2} .19}$ là:

A. 3².7²

B. 3³.7³.11.19

C. 3².7².11.19

D. 3³.7².11.19

Xem đáp án

BCNNBCNN hay mẫu chung nguyên dương nhỏ nhất của hai mẫu đã cho là

3³.7².11.19

Đáp án cần chọn là: D

Câu 42:

Nhân cả tử số và mẫu số của phân số $\frac{14}{23}$ với số nào để được phân số $\frac{168}{276}$ ?

A. 14

B. 23

C. 12

D. 22

Xem đáp án

Ta có: 168:14 = 12 và 276:23 = 12 nên số cần tìm là 12

Đáp án cần chọn là: C

Câu 43:

Phân số bằng phân số $\frac{301}{403}$ mà có tử số và mẫu số đều là số dương, có ba chữ số là phân số nào?

A. $\frac{151}{201}$

B. $\frac{602}{806}$

C. $\frac{301}{403}$

D. $\frac{903}{1209}$

Xem đáp án

Ta có:

+) $\frac{301}{403} = \frac{301.2}{403.2} = \frac{602}{806} (T M)$

+) $\frac{301}{403} = \frac{301.3}{403.3} = \frac{903}{1209} (L)$

Do đó ở các trường hợp nhân cả tử và mẫu với một số tự nhiên lớn hơn 33 ta cũng đều loại được.

Ngoài ra phân số $\frac{301}{403}$ tối giản nên không thể rút gọn được.

Vậy phân số cần tìm là $\frac{602}{806}$

Đáp án cần chọn là: B

Câu 44:

Tìm x biết $\frac{- 5}{- 14} = \frac{20}{6 - 5 x}$

A. x = 10

B. x = −10

C. x = 5

D. x = 6

Xem đáp án

Ta có:

$\frac{- 5}{- 14} = \frac{(- 5) . (- 4)}{(- 14) . (- 4)} = \frac{20}{56} = \frac{20}{6 - 5 x}$

⇒56=6−5x56−6=−5x50=−5xx=50:(−5)x=−10⇒56=6−5x56−6=−5x50=−5xx=50:(−5)x=−10

Đáp án cần chọn là: B

Câu 45:

Biểu thức $\frac{5^{12} {.3}^{9} - 5^{10} {.3}^{11}}{5^{10} {.3}^{10}}$ sau khi đã rút gọn đến tối giản có mẫu số dương là:

A. 16

B. 3

C.

\frac{16}{5}

D.

\frac{16}{3}

Xem đáp án

$\frac{5^{12} {.3}^{9} - 5^{10} {.3}^{11}}{5^{10} {.3}^{10}} = \frac{5^{10} {.3}^{9} (5^{2} - 3^{2})}{5^{10} {.3}^{10}} = \frac{5^{10} {.3}^{9} .16}{5^{10} {.3}^{10}} = \frac{16}{3}$

Vậy mẫu số của phân số đó là 3

Đáp án cần chọn là: B

Câu 46:

Sau khi rút gọn biểu thức $\frac{5^{11} {.7}^{12} + 5^{11} {.7}^{11}}{5^{12} {.7}^{12} + {9.5}^{11} {.7}^{11}}$ ta được phân số $\frac{a}{b}$ . Tính tổng a + b

A. 26

B. 13

C. 52

D. 8

Xem đáp án

$\frac{5^{11} {.7}^{12} + 5^{11} {.7}^{11}}{5^{12} {.7}^{12} + {9.5}^{11} {.7}^{11}} = \frac{5^{11} {.7}^{11} (7 + 1)}{5^{11} {.7}^{11} (5.7 + 9)} = \frac{8}{44} = \frac{2}{11}$

Do đó a=2,b=11 nên a+b=13

Đáp án cần chọn là: B

Câu 47:

Tìm phân số bằng với phân số $\frac{200}{520}$ mà có tổng của tử và mẫu bằng 306.

A. $\frac{84}{222}$

B. $\frac{200}{520}$

C. $\frac{85}{221}$

D. $\frac{100}{260}$

Xem đáp án

Ta có:

$\frac{200}{520} = \frac{5}{13}$ nên có dạng tổng quát là $\frac{5 k}{13 k} (k \in Z, k \neq 0)$

Do tổng và tử và mẫu của phân số cần tìm bằng 306 nên:

5k + 13k = 306

18k = 306

k 306:18

k = 17

Vậy phân số cần tìm là

$\frac{5.17}{13.17} = \frac{85}{221}$

Đáp án cần chọn là: C

Câu 48:

Viết dạng tổng quát của các phân số bằng với phân số $\frac{- 12}{40}$

A.

B.

C.

D.

A. $\frac{- 3 k}{10 k}, k \in Z$

B. $\frac{- 3 k}{10}, k \in Z, k \neq 0$

C. $\frac{- 3 k}{10 k}, k \in Z, k \neq 0$

D. $\frac{- 3}{10}$

Xem đáp án

- Rút gọn phân số: $\frac{- 12}{40} = \frac{- 12 : 4}{40 : 4} = \frac{- 3}{10}$

- Dạng tổng quát của phân số đã cho là: $\frac{- 3 k}{10 k}, k \in Z, k \neq 0$

Đáp án cần chọn là: C

Câu 49:

Tìm phân số tối giản $\frac{a}{b}$ biết rằng lấy tử cộng với 6, lấy mẫu cộng với 14 thì ta được phân số bằng 37.

A. $\frac{4}{5}$

B. $\frac{7}{3}$

C. $\frac{- 3}{7}$

D. $\frac{3}{7}$

Xem đáp án

Ta có:

$\frac{a + 6}{b + 14} = \frac{3}{7}$ 7.(a+6)=3.(b+14)

7a+42=3b+42

7a=3b

$\frac{a}{b} = \frac{3}{7}$

Đáp án cần chọn là: C

Câu 50:

Cho các phân số $\frac{6}{n + 8}; \frac{7}{n + 9}; \frac{8}{n + 10}; ...; \frac{35}{n + 37}$ . Tìm số tự nhiên n nhỏ nhất để các phân số trên tối giản

A. 35

B. 34

C. 37

D. 36

Xem đáp án

Các phân số đã cho đều có dạng

$\frac{a}{a + (n + 2)}$

Và tối giản nếu a và n + 2 nguyên tố cùng nhau

Vì: [a + (n + 2)] – a = n + 2 với a = 6; 7; 8;.....; 34; 35

Do đó n + 2 nguyên tố cùng nhau với các số 6; 7; 8;.....; 34; 35

Số tự nhiên n + 2 nhỏ nhất thỏa mãn tính chất này là 37

Ta có n + 2 = 37 nên n = 37 – 2 = 35

Vậy số tự nhiên nhỏ nhất cần tìm là 35

Đáp án cần chọn là: A

Câu 51:

Quy đồng mẫu số các phân số

\frac{11}{12}; \frac{15}{16}; \frac{23}{20}

ta được các phân số lần lượt là:

A. $\frac{220}{240}; \frac{225}{240}; \frac{276}{240}$

B. $\frac{225}{240}; \frac{220}{240}; \frac{276}{240}$

C. $\frac{225}{240}; \frac{276}{240}; \frac{220}{240}$

D. $\frac{220}{240}; \frac{276}{240}; \frac{225}{240}$

Xem đáp án

Ta có:

12 = 2².3; 16 = 2⁴; 20 = 2².5

Do đó MSC = 2⁴.3.5 = 240

$\frac{11}{12} = \frac{11.20}{12.20} = \frac{220}{240};$

$\frac{15}{16} = \frac{15.15}{16.15} = \frac{225}{240};$

$\frac{23}{20} = \frac{23.12}{20.12} = \frac{276}{240};$

Vậy các phân số sau khi quy đồng lần lượt là: $\frac{220}{240}; \frac{225}{240}; \frac{276}{240}$

Đáp án cần chọn là: A

Câu 52:

Rút gọn rồi quy đồng mẫu số các phân số $\frac{3.4 - 3.7}{6.5 + 9}$ và $\frac{6.9 - 2.17}{63.3 - 119}$ ta được

A. $\frac{- 21}{91}, \frac{26}{91}$

B. $\frac{- 3}{13}, \frac{2}{7}$

C. $\frac{21}{91}, \frac{26}{91}$

D. $\frac{- 21}{91}, \frac{36}{91}$

Xem đáp án

$\frac{3.4 - 3.7}{6.5 + 9} = \frac{12 - 21}{30 + 9} = \frac{- 9}{39} = \frac{- 3}{13}$

$\frac{6.9 - 2.17}{63.3 - 119} = \frac{54 - 34}{189 - 119} = \frac{20}{70} = \frac{2}{7}$

MSC = 91

$\frac{- 3}{13} = \frac{- 3.7}{13.7} = \frac{- 21}{91};$

$\frac{2}{7} = \frac{2.13}{7.13} = \frac{26}{91}$

Vậy sau khi quy đồng ta được hai phân số $\frac{- 21}{91}, \frac{26}{91}$

Đáp án cần chọn là: A

Trắc nghiệm Toán 6 CD Bài 1: Phân số với tử và mẫu là số nguyên có đáp án

Trắc nghiệm Toán 6 CD Bài 1: Phân số với tử và mẫu là số nguyên có đáp án

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương