10 câu hỏi trắc nghiệm thuộc Dạng 1: Xác định, chứng minh đường thẳng song song mặt phẳng có đáp án

Trắc nghiệm Toán 11 Bài 12: Đường thẳng và mặt phẳng song song có đáp án

Dạng 1: Xác định, chứng minh đường thẳng song song mặt phẳng có đáp án

107 lượt thi
10 câu hỏi
0 phút

Danh sách câu hỏi

Câu 1:

Cho hình bình hành ABCD và một điểm S không nằm trên (ABCD), E và F là hai điểm trên SA; SB sao cho: $\frac{S E}{S A} = \frac{S F}{S B} = \frac{1}{3}$ . Vị trí tương đối giữa EF và (ABCD) là

D. EF và (ABCD) chéo nhau.

A. EF nằm trên (ABCD);

B. EF cắt (ABCD);

C. EF song song (ABCD);

D. EF và (ABCD) chéo nhau.

Xem đáp án

Đáp án đúng là: C

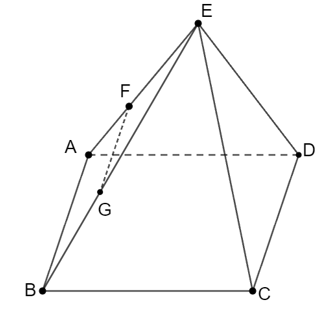
Cho hình bình hành ABCD và một điểm S không nằm trên (ABCD), E và F là hai điểm trên SA; SB (ảnh 1)

Theo định lí Thalès, ta có:

$\frac{S E}{S A} = \frac{S F}{S B} = \frac{1}{3}$ nên EF song song với AB

Mà AB nằm trong mặt phẳng (ABCD) nên: EF // (ABCD).

Câu 2:

Cho tứ diện ABCD. G là trọng tâm của tam giác ABD; M nằm trên AB sao cho AM = 2MB. Vị trí tương đối của MG và (BCD) là

A. MG nằm trên (BCD);

B. MG cắt (BCD);

C. MG song song (BCD);

D. MG và (BCD) chéo nhau.

Xem đáp án

Đáp án đúng là: C

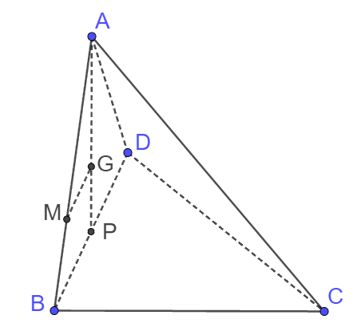
Cho tứ diện ABCD. G là trọng tâm của tam giác ABD; M nằm trên AB sao cho AM = 2MB. Vị trí tương đối của MG và (BCD) là (ảnh 1)

Từ (1) và (2) suy ra: $\frac{A G}{A P} = \frac{A M}{A B}$ .

Do đó MG // BD (định lí Thalès đảo)

Mặt khác BD nằm trong mặt phẳng (BCD) suy ra GQ // mp(BCD).

Câu 3:

Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD. Trên BC lấy điểm E sao cho EB = 2EC. Vị trí tương đối của EG và (ACD) là

A. EG nằm trên (ACD);

B. EG song song (ACD);

C. EG cắt (ACD);

D. EG và (ACD) chéo nhau.

Xem đáp án

Đáp án đúng là: B

Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD. Trên BC lấy điểm E sao cho EB = 2EC. Vị trí tương đối của EG và (ACD) là (ảnh 1)

Gọi I là trung điểm AD.

G là trọng tâm tam giác ABD nên $\frac{B G}{B I} = \frac{2}{3}$ (1)

Điểm E nằm trên BC sao cho EB = 2EC nên $\frac{B E}{B C} = \frac{2}{3}$ (2)

Từ (1) và (2) ta có EG // CI (Định lý Thalès).

Mà CI nằm trong mặt phẳng (ACD).

Vậy EG // (ACD).

Câu 4:

Cho tứ diện ABCD. Gọi E, E lần lượt là trung điểm của AB, AC. Vị trí tương đối của EF và (BCD) là

A. EF song song (BCD);

B. EF nằm trên (BCD);

C. EF vuông góc (BCD);

D. EF cắt (BCD).

Xem đáp án

Đáp án đúng là: A

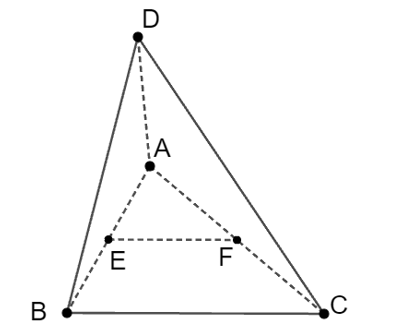
Cho tứ diện ABCD. Gọi E, E lần lượt là trung điểm của AB, AC. Vị trí tương đối của EF và (BCD) là (ảnh 1)

Do E và F là trung điểm của AB và AC nên EF // BC (tính chất đường trung bình của tam giác).

Mà BC nằm trên mặt phẳng (BCD) nên EF // (BCD).

Câu 5:

Cho tứ diện ABCD. Gọi E, F là trọng tâm các tam giác ACD và ABD. Vị trí tương đối của EF và ABC là

A. EF song song (ABC);

B. EF nằm trên (ABC);

C. EF vuông góc (ABC);

D. EF cắt (ABC).

Xem đáp án

Đáp án đúng là: A

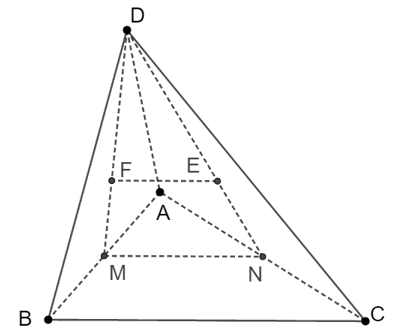
Cho tứ diện ABCD. Gọi E, F là trọng tâm các tam giác ACD và ABD. Vị trí tương đối của EF và ABC là (ảnh 1)

Gọi M và N lần lượt là trung điểm của AB và AC.

E và F là trọng tâm các tam giác ACD và ABD nên EF // MN.

Mà MN nằm trên (ABC) nên EF // (ABC).

Câu 6:

Cho hình chóp S.ABC; gọi G; H là trọng tâm tam giác SAC và SBC. Gọi M là trung điểm của BC. Đường thẳng song song với (ABC) là

A. GM;

B. HM;

C. GH;

D. GS.

Xem đáp án

Đáp án đúng là: C

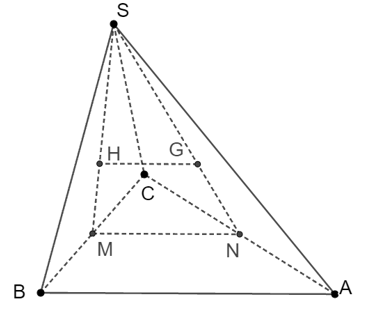
Cho hình chóp S.ABC; gọi G; H là trọng tâm tam giác SAC và SBC. Gọi M là trung điểm của BC (ảnh 1)

Gọi M và N là trung điểm của BC và AC.

Do G; H lần lượt là trọng tâm tam giác SAC và SBC nên $\frac{S H}{S M} = \frac{S G}{S N} = \frac{2}{3}$

Suy ra GH // HK.

Mà HK ⊂ (ABC) nên GH // (ABC).

Câu 7:

Cho tứ diện ABCD; lấy điểm M trên cạnh AB sao cho: $\frac{A M}{A B} = \frac{1}{4}$ . Trên cạnh AC lấy điểm N sao cho MN // (BCD). Tỉ số $\frac{A N}{N C}$ là

A. $\frac{1}{2}$

B. $\frac{1}{3}$

C. 2

D. 3

Xem đáp án

Đáp án đúng là: B

Cho tứ diện ABCD; lấy điểm M trên cạnh AB sao cho: AM/AB=1/4. Trên cạnh AC lấy điểm N sao cho MN // (BCD). (ảnh 1)

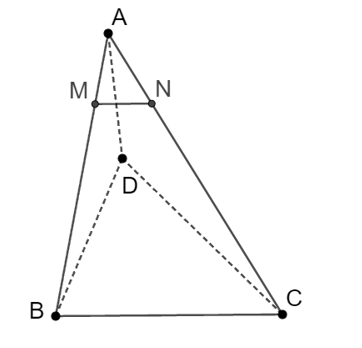
Giả sử MN cắt BC tại P.

Ta có BC ⊂ (BCD) nên đường thẳng MN cắt (BCD) tại P (mâu thuẫn với đề bài MN // (BCD)).

Do đó MN // BC.

Xét tam giác ABC có MN // BC, theo định lí Thalès ta có

$\frac{A M}{A B} = \frac{A N}{A C} = \frac{1}{4}$ hay $\frac{A N}{N C} = \frac{1}{3}$ .

Câu 8:

Cho hình bình hành ABCD và điểm S không nằm trên (ABCD). Gọi E, F, G và H lần lượt là trung điểm của AB, CD, SA và SD. Mặt phẳng song song với đường thẳng EF là

A. (GBA);

B. (HCD);

C. (GHB);

D. (HAB).

Xem đáp án

Đáp án đúng là: C

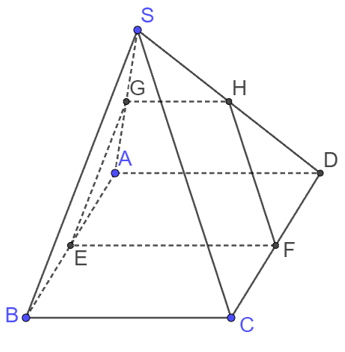
Cho hình bình hành ABCD và điểm S không nằm trên (ABCD). Gọi E, F, G và H lần lượt là trung điểm của AB, CD, SA và SD (ảnh 1)

• Xét mp (ABCD) có E và F lần lượt là trung điểm của AB và CD.

Nên EF là đường trung bình của hình bình hành

Do đó EF // AD // BC (1)

• Xét tam giác SAD có G và H lần lượt là trung điểm của SA và SD.

Nên GH là đường trunh bình của tam giác SAD.

Do đó GH // AD (2)

Từ (1) và (2) suy ra: GH // EF // AD // BC.

Vậy EF // mp(GHB).

Câu 9:

Cho hình bình hành ABCD và điểm S không nằm trên (ABCD). O là giao điểm của AC và BD. I là trung điểm của SC. Đường thẳng song song với (SAB) là

A. SI;

B. IC;

C. SO;

D. IO.

Xem đáp án

Đáp án đúng là: D

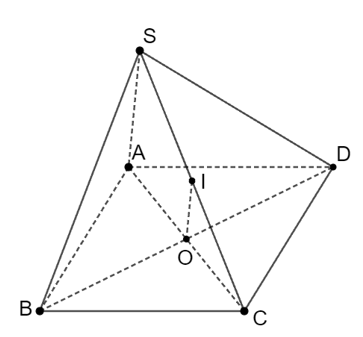
Cho hình bình hành ABCD và điểm S không nằm trên (ABCD). O là giao điểm của AC và BD. I là trung điểm của SC (ảnh 1)

O là giao điểm của AC và BD nên O là trung điểm của AC.

Mà I là trung điểm của SC nên IO // SA (đường trung bình của tam giác SAC).

Mà SA nằm trên SAB nên IO // (SAB).

Câu 10:

Cho a và b là hai đường thẳng chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b?

A. 0;

B. 1;

C. 2;

D. vô số.

Xem đáp án

Đáp án đúng là: D

Với hai đường thẳng chéo nhau, khi đó có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.

Bắt đầu thi ngay

Trắc nghiệm Toán 11 Bài 12: Đường thẳng và mặt phẳng song song có đáp án

Dạng 1: Xác định, chứng minh đường thẳng song song mặt phẳng có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương