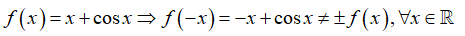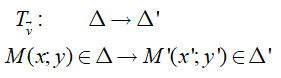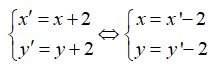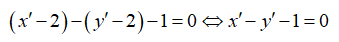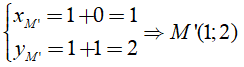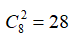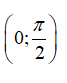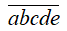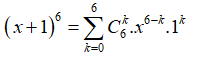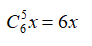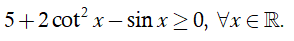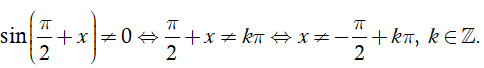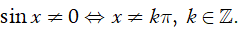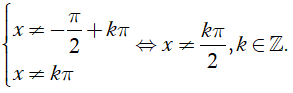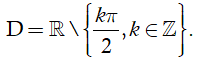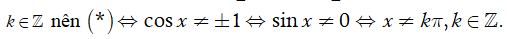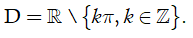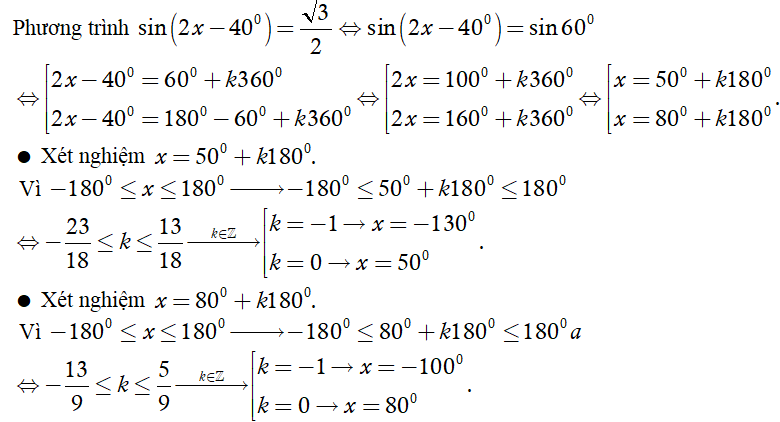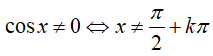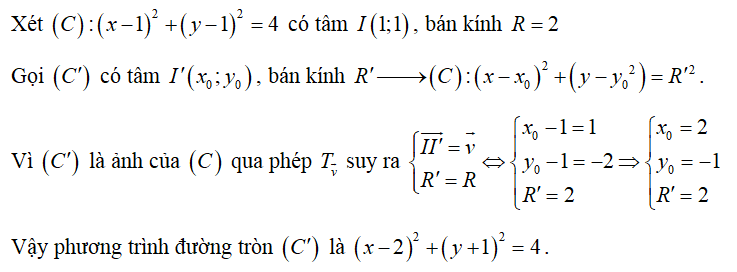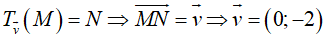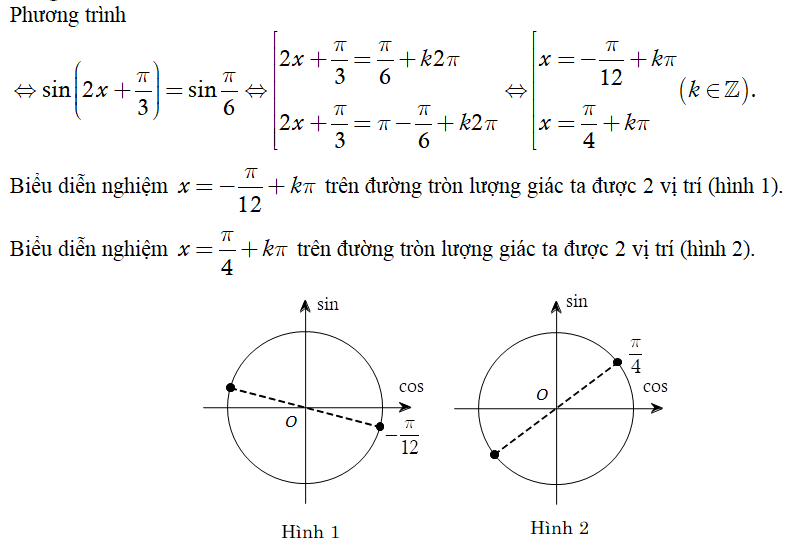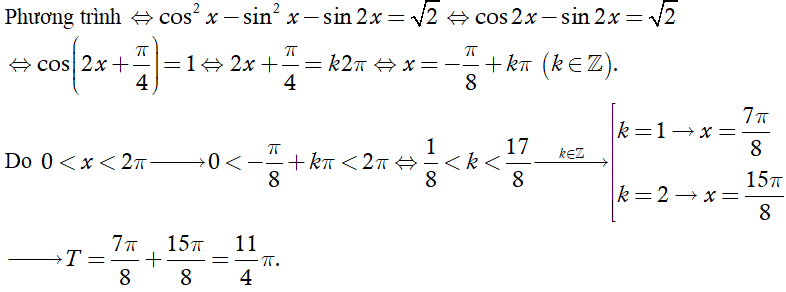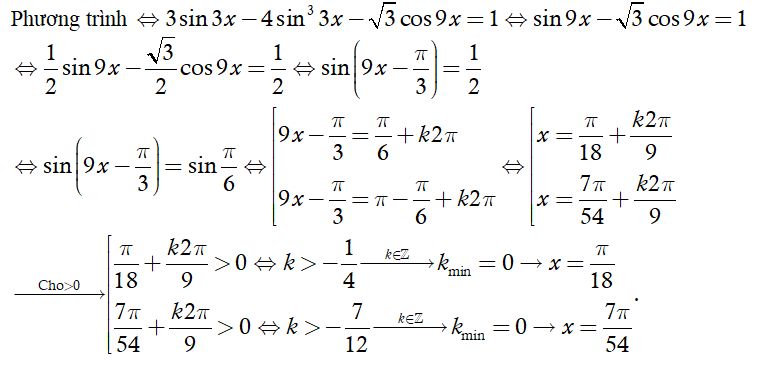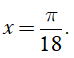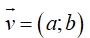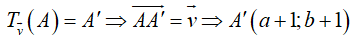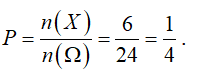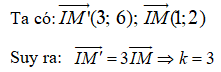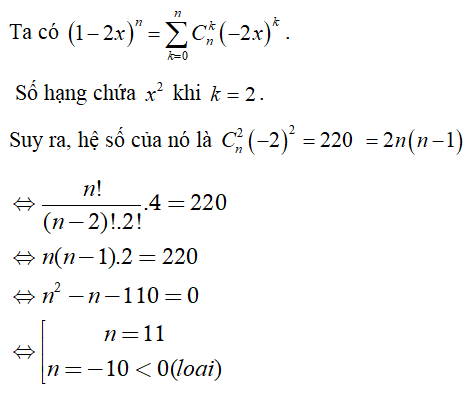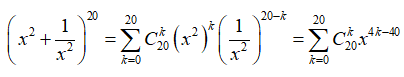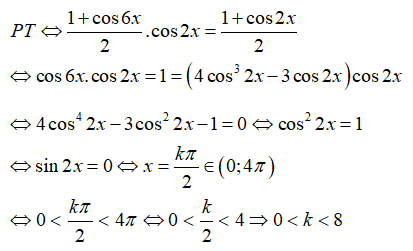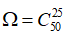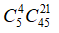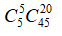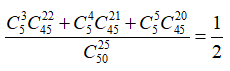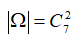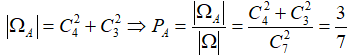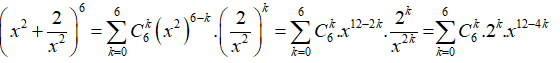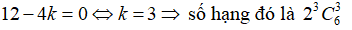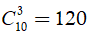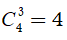Đề thi Học kì 1 Toán lớp 11 năm 2020 - 2021 có đáp án (Đề 2)
-
213 lượt thi
-
50 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M(1;0) . Phép quay tâm O góc 90 biến điểm M thành M’ có tọa độ là
 Xem đáp án
Xem đáp án
Đáp án B
Câu 4:
Khẳng định nào sau đây là sai ?
 Xem đáp án
Xem đáp án
Chọn A
Xét phương án A:
Ta có
Do đó; hàm số y = x + cosx là hàm số không chẵn; không lẻ
Câu 5:
Trong mặt phẳng với hệ tọa độ Oxy. Phép tịnh tiến theo vectơ = (2;2) biến đường thẳng Δ: x - y -1 = 0 thành đường thẳng Δ' có phương trình là
 Xem đáp án
Xem đáp án
Chọn A
Ta có:
Vì điểm M thuộc đường thẳng Δ nên : x – y – 1 = 0 (*)
Thay vào (*) ta được:
Câu 6:
Trong mặt phẳng với hệ tọa độ Oxy, điểm M(1;1) . Phép tịnh tiến theo vectơ v = (0,1) biến M thành điểm M’ có tọa độ là
 Xem đáp án
Xem đáp án
Chọn C
Ta có:
Câu 7:
Trong các mệnh đề sau, mệnh đề nào đúng ?
 Xem đáp án
Xem đáp án
Chọn B
Ta có A sai vì nếu điểm đó thuộc đường thẳng thì sẽ có vô số mặt phẳng.
+) B đúng
+) C sai (suy ra từ A).
+) D sai (suy ra từ A).
Câu 8:
Có 8 đội bóng chuyền nữ thi đấu theo thể thức vòng tròn (hai đội bóng chuyền bất kì chỉ gặp nhau một lần) và tính điểm. Số trận đấu được tổ chức là
 Xem đáp án
Xem đáp án
Chọn A
Số trận đấu được tổ chức là:
Câu 9:
Giả sử một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiện, hành động kia có n cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất. Công việc đó có
 Xem đáp án
Xem đáp án
Chọn C
Công việc đó có m + n cách thực hiện.
Câu 12:
Từ các chữ số 1, 2,3, 4,5, 6, 7 và 8 lập được bao nhiêu số gồm 5 chữ số khác nhau đôi một?
 Xem đáp án
Xem đáp án
Chọn B
Gọi số có 5 chữ số thỏa mãn đầu bài là:
+ chọn a có 8 cách
+ Chọn b: có 7 cách
+ Chọn c có 6 cách
+ Chọn d co 5 cách
+ Chọn e có 4 cách
Theo quy tắc nhân có 8.7.6.5.4 = 6720 số thỏa mãn.
Câu 13:
Số hạng chứa x trong khai triển của biểu thức (x + 1) là
 Xem đáp án
Xem đáp án
Chọn D
Ta có
Số hạng chứa x cần thỏa mãn:
6 - k = 1 ⇒ k = 5
Vậy số hạng chứa x là:
Câu 14:
Tìm tập xác định D của hàm số
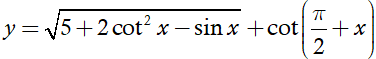
 Xem đáp án
Xem đáp án
Chọn A
Hàm số xác định khi và chỉ khi các điều kiện sau thỏa mãn đồng thời
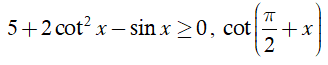
Ta có
⇒
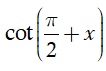
cot x xác định
Do đó hàm số xác định
Vậy tập xác định
Câu 15:
Tìm tập xác định D của hàm số
 Xem đáp án
Xem đáp án
Chọn D
Hàm số xác định khi và chỉ khi 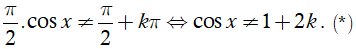
Do
Vậy tập xác định
Câu 18:
Trong mặt phẳng với hệ tọa độ Oxy . Phép tịnh tiến theo vectơ (1;-2) biến đường tròn thành đường tròn (C') có phương trình
 Xem đáp án
Xem đáp án
Chọn C
Câu 19:
Trong mặt phẳng với hệ tọa độ Oxy, điểm M(1;1) N(1;-1) . Phép tịnh tiến theo vectơ v biến M thành điểm N. Khi đó ta có
 Xem đáp án
Xem đáp án
Chọn D
Ta có :
Câu 20:
Số vị trí biểu diễn các nghiệm của phương trình trên đường tròn lượng giác là?
 Xem đáp án
Xem đáp án
Chọn C
Câu 22:
Tìm nghiệm dương nhỏ nhất của
 Xem đáp án
Xem đáp án
Chọn B
So sánh hai nghiệm ta được nghiệm dương nhỏ nhất là
Câu 23:
Trên bàn có 8 cây bút chì khác nhau, 6 cây bút bi khác nhau và 10 cuốn tập khác nhau. Một học sinh muốn chọn một đồ vật duy nhất hoặc một cây bút chì hoặc một cây bút bi hoặc một cuốn tập thì số cách chọn khác nhau là:
 Xem đáp án
Xem đáp án
Chọn B
Nếu chọn một cây bút chì thì sẽ có 8 cách.
Nếu chọn một cây bút bi thì sẽ có 6 cách.
Nếu chọn một cuốn tập thì sẽ có 10 cách.
Theo qui tắc cộng, ta có 8+ 6 + 10 = 24cách chọn
Câu 24:
Một bó hoa có 5 hoa hồng trắng, 6 hoa hồng đỏ và 7 hoa hồng vàng. Hỏi có mấy cách chọn lấy ba bông hoa có đủ cả ba màu.
 Xem đáp án
Xem đáp án
Chọn B
Để chọn ba bông hoa có đủ cả ba màu (nghĩa là chọn một bông hoa hồng trắng- một bông hoa hồng đỏ- hoa hồng vàng), ta có:
Có 5 cách chọn hoa hồng trắng.
Có 6 cách chọn hoa hồng đỏ.
Có 7 cách chọn hoa hồng vàng.
Vậy theo qui tắc nhân ta có 5.6.7 = 210 cách.
Câu 25:
Trong mặt phẳng với hệ tọa độ Oxy. Phép tịnh tiến theo vectơ v biến đường thẳng d: x+2y-3=0 thành đường thẳng d': x+2y-7=0. Khi đó ta có
 Xem đáp án
Xem đáp án
Chọn C
Lấy A(1;1)∈ d và vectơ
Ta có
Vì A’ thuộc d’ suy ra a + 1 + 2(b + 1) - 7 = 0 ⇔ a + 2ab = 4 .
Trong các phương án chỉ có phương án C thỏa mãn
Câu 26:
Tìm mệnh đề sai trong các mệnh đề sau
 Xem đáp án
Xem đáp án
Chọn D
Mệnh đề: A, B, C đúng.
Mệnh đề D chỉ đúng khi đường thẳng nằm trong mặt phẳng , còn khi đường thẳng cắt mặt phẳng tại một điểm thì mệnh đề trên là sai .
Câu 27:
Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất hai lần. Xác suất để ít nhất một lần xuất hiện mặt hai chấm là
 Xem đáp án
Xem đáp án
Chọn A
TH1: Gieo lần 1 xuất hiện mặt 2 chấm, lần 2 không xuất hiện mặt 2 chấm ⇒ có 5 cách.
TH2: Gieo lần 1 không xuất hiện mặt 2 chấm, lần 2 xuất hiện mặt 2 chấm ⇒ có 5 cách.
H3: Gieo cả 2 lần đều được mặt 2 chấm ⇒ có 1 cách.
Vậy xác suất cần tính là 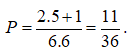
Câu 28:
Trong mặt phẳng với hệ tọa độ Oxy, phép vị tự tâm O tỉ số k = 2 biến đường thẳng x + y = 0 thành đường thẳng nào trong các đường thẳng có phương trình sau ?
 Xem đáp án
Xem đáp án
Chọn B
Gọi d': x + y + m = 0 là ảnh của d’ qua phép vị tự tâm O.
Vì O ∈ d suy ra O chính là ảnh của O qua V(O;k) .
Vậy (d'): x + y = 0 .
Câu 30:
Xếp 2 học sinh nam khác nhau và 2 học sinh nữ khác nhau vào một hàng ghế dài có 6 chỗ ngồi sao cho 2 học sinh nam ngồi kề nhau và 2 học sinh nữ ngồi kề nhau. Hỏi có bao nhiêu cách ?
 Xem đáp án
Xem đáp án
Chọn B
Coi 2 bạn nam ngồi cạnh nhau là 1 phần tử X, 2 bạn nữ ngồi cạnh nhau là 1 phần tử Y.
Chọn 2 ghế từ 4 ghế để xếp 2 phần tử X; Y có: 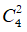
Đổi chỗ 2 bạn nữ ta có them 1 cách. Nên số cách xếp 2 bạn nữ trong Y là 2.
Số cách xếp 2 bạn nam trong X là 2
Theo quy tắc nhân, có tất cả 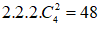
Câu 31:
Lấy ngẫu nhiên một thẻ từ một hộp chứa 24 thẻ được đánh số từ 1 đến 24. Xác suất để thẻ lấy được ghi số chia hết cho 4 là :
 Xem đáp án
Xem đáp án
Chọn C
Lấy ngẫu nhiên 1 thẻ trong 24 thẻ có 24 cách suy ra n(Ω) = 24 .
Trong các số từ 1 đến 24 có số {4;8;12;16;20;24} chia hết cho 4.
Suy ra số kết quả thuận lợi cho biến cố là n(X) = 6 .
Vậy
Câu 32:
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Giao tuyến của hai mặt phẳng (SAB) và (SCD) là:
 Xem đáp án
Xem đáp án
Chọn D
Xét giao tuyến của 2 mặt phẳng ( SAB) và (SCD) có:
S chung
AB// CD
AB ⊂ (SAB) ; CD ⊂ (SCD)
Suy ra giao tuyến của hai mặt phẳng (SAB), (SCD) là đường thẳng đi qua S và song song với đường thẳng CD.
Câu 33:
Trong mặt phẳng với hệ tọa độ Oxy, phép vị tự tâm I(1;2) tỉ số k biến điểm M(3;3) thành điểm M'(5;7) . Khi đó k bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn D
Câu 34:
Biết hệ số của số hạng chứa x2 trong khai triển của biểu thức là 220. Tìm n ?
 Xem đáp án
Xem đáp án
Chọn A
Câu 35:
Số hạng không chứa x trong khai triển của biểu thức là:
 Xem đáp án
Xem đáp án
Chọn D
Ta có
Số hạng không chứa x khi k = 10 , hệ số của nó là 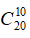
Câu 38:
Đề cương ôn tập cuối năm môn Toán lớp 11 có 50 câu hỏi. Đề thi cuối năm gồm 5 câu trong số 50 câu đó. Một học sinh chỉ ôn 25 câu trong đề cương. Giả sử các câu hỏi trong đề cương đều có khả năng được chọn làm câu hỏi thi như nhau. Xác suất để có ít nhất 3 câu hỏi của đề thi cuối năm nằm trong số 25 câu hỏi mà học sinh nói trên đã ôn tập là :
 Xem đáp án
Xem đáp án
Chọn C
Không gian mẫu là
Giả sử trong 25 câu có 3 câu hỏi đề thi: 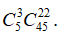
Giả sử trong 25 câu có 4 câu hỏi đề thi:
Giả sử trong 25 câu có 5 câu hỏi đề thi:
Xác suất cần tìm là:
Câu 39:
Sắp xếp năm bạn học sinh An, Bình, Chi, Dũng, Lệ vào một chiếc ghế dài có 5 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho bạn An và bạn Dũng luôn ngồi ở hai đầu ghế?
 Xem đáp án
Xem đáp án
Chọn C
Xếp An và Dũng ngồi hai đầu ghế có 2! cách xếp.
Số cách xếp 3 bạn Bình, Chi, Lệ vào 3 ghế còn lại là một hoán vị của 3 phần tử nên có có 3! cách.
Vậy có 2!.3! = 12 cách.
Câu 40:
Trên giá sách muốn xếp 20 cuốn sách khác nhau, trong đó có cuốn sách tập 1 và cuốn sách tập 2. Có bao nhiêu cách xếp sao cho cuốn sách tập 1 và tập 2 không nằm cạnh nhau.
 Xem đáp án
Xem đáp án
Chọn D
• Sắp xếp 20 cuốn sách trên giá là một hoán vị của 20 phần tử nên ta có
20! cách sắp xếp.
• Khi hai cuốn tập 1 và tập 2 đặt cạnh nhau (thay đổi vị trí cho nhau), ta coi đó là một phần tử và cùng sắp xếp với 18 cuốn sách còn lại trên giá nên có 2. 19! cách sắp xếp.
Vậy có tất cả 20! - 2.19! = 19!.18 cách sắp xếp theo yêu cầu bài toán.
Câu 41:
Một thùng có 7 sản phầm, trong đó có 4 sản phầm loại I và 3 sản phầm loại II. Lấy ngẫu nhiên 2 sản phẩm. Xác suất để lấy được 2 sản phẩm cùng loại là
 Xem đáp án
Xem đáp án
Chọn B
Không gian mẫu là
Không gian biến cố là
Câu 43:
Cho tập A = {0,1,2......9} Số các số tự nhiên có 5 chữ số đôi một khác nhau lấy ra từ tập A là?
 Xem đáp án
Xem đáp án
Chọn C
Gọi số cần tìm là 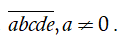
Chọn a có 9 cách.
Chọn b; c; d; e từ 9 số còn lại có 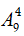
Vậy có 9. 3024 = 27216.
Câu 44:
Có bao nhiêu số tự nhiên gồm 7 chữ số khác nhau đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3?
 Xem đáp án
Xem đáp án
Chọn B
Ta chia thành các trường hợp sau:
TH1: Nếu số 123 đứng đầu thì có 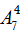
TH2: Nếu số 321 đứng đầu thì có 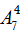
TH3: Nếu số 123; 321 không đứng đầu
Khi đó có 6 cách chọn số đứng đầu ( khác 0; 1; 2; 3 ).
khi đó còn 6 vị trí:
có 4 cách xếp 3 số 321 hoặc 123, còn lại 3 vị trí có 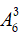
Do đó trường hợp này có 6.2.4.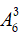
Suy ra tổng các số thoả mãn yêu cầu là 2.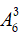
Câu 45:
Trong một ban chấp hành đoàn gồm 7 người, cần chọn 3 người trong ban thường vụ. Nếu không có sự phân biệt về chức vụ của 3 người trong ban thường vụ thì có bao nhiêu các chọn?
 Xem đáp án
Xem đáp án
Chọn D
Vì không xét đến sự phân biệt chức vụ của 3 người trong ban thường vụ nên mỗi cách chọn ứng với một tổ hợp chập 3 của 7 phần tử.
Như vậy, ta có 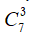
Câu 46:
Trong mặt phẳng cho tập hợp P gồm 2018 điểm phân biệt. Hỏi có bao nhiêu đoạn thẳng mà hai đầu mút thuộc P ?
 Xem đáp án
Xem đáp án
Chọn D
Với hai điểm bất kỳ trong n điểm ta luôn được một đoạn thẳng.
Vậy số đoạn thẳng cần tìm chính là một tổ hợp chập 2 của 2018 phần tử (điểm).
Như vậy, ta có 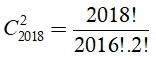
Câu 47:
Cho 10 điểm phân biệt A1; A2;....;A100 trong đó có 4 điểm A1;A2;A3;A4 thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác có 3 đỉnh được lấy trong 10 điểm trên?
 Xem đáp án
Xem đáp án
Chọn C
Số cách lấy 3 điểm từ 10 điểm phân biệt là
Số cách lấy 3 điểm bất kì trong 4 điểm A1 ; A2 ; A3 ; A4 là
Khi lấy 3 điểm bất kì trong 4 điểm A1 ; A2 ; A3 ; A4 thì sẽ không tạo thành tam giác.
Câu 48:
Cho hai đường thẳng song song d1 và d2 . Trên d1 lấy 17 điểm phân biệt, trên d2 lấy 20 điểm phân biệt. Tính số tam giác mà có các đỉnh được chọn từ 37 điểm này.
 Xem đáp án
Xem đáp án
Chọn C
Một tam giác được tạo bởi ba điểm phân biệt nên ta xét:
TH1. Chọn 1 điểm thuộc d1 và 2 điểm thuộc d2 có 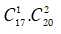
TH2. Chọn 2 điểm thuộc d1 và 1 điểm thuộc d2 có 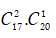
Như vậy, ta có 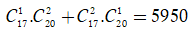
Câu 49:
Số giao điểm tối đa của 5 đường tròn phân biệt là:
 Xem đáp án
Xem đáp án
Chọn B
Hai đường tròn cho tối đa hai giao điểm.
Và 5 đường tròn phân biệt cho số giao điểm tối đa khi 2 đường tròn bất kỳ trong 5 đường tròn đôi một cắt nhau.
Vậy số giao điểm tối đa của 5 đường tròn phân biệt là