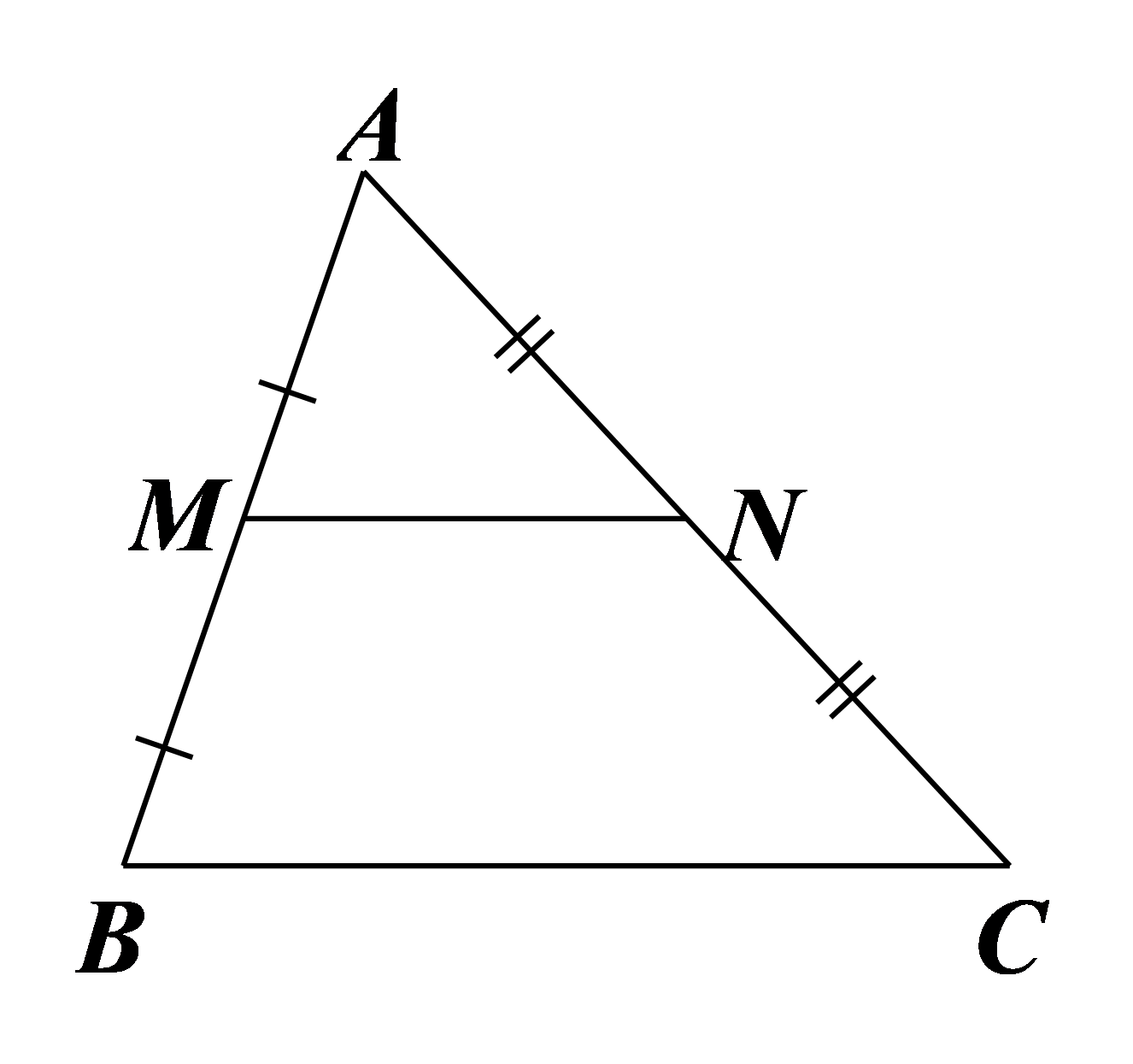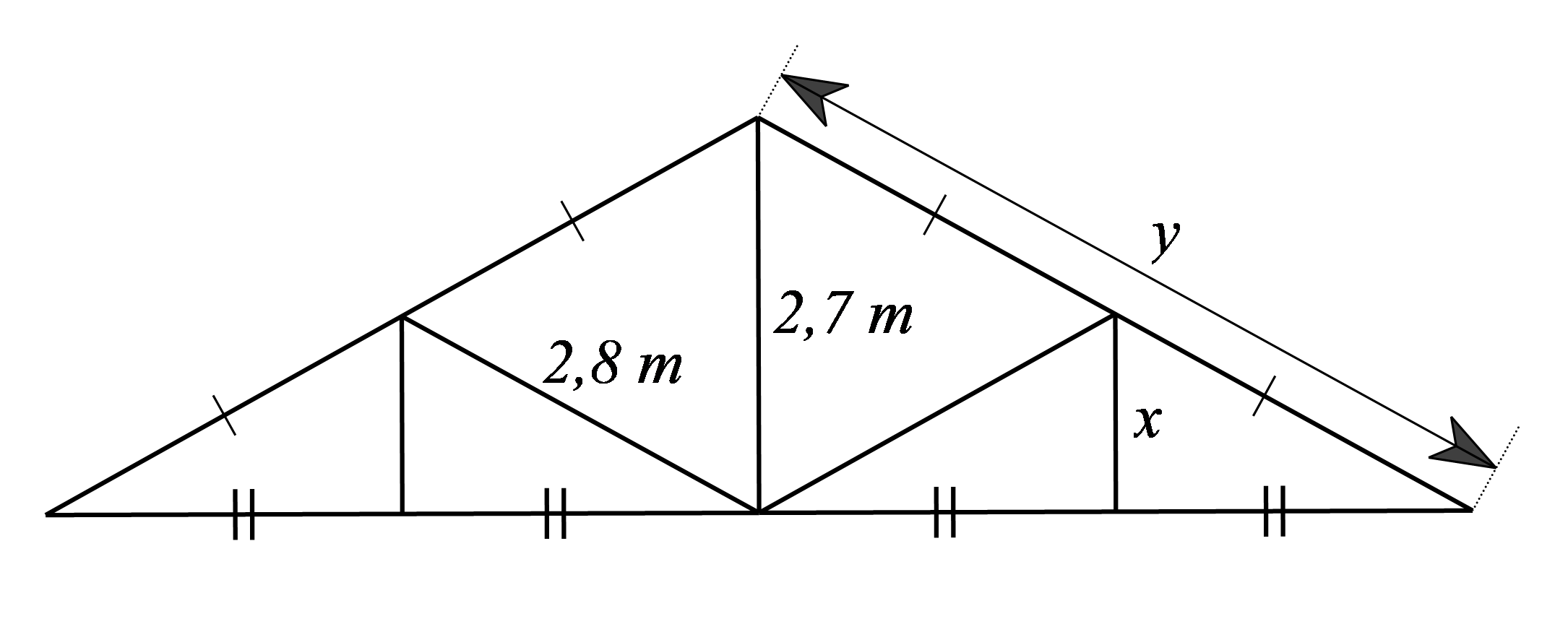10 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa kì 2 Toán 8 CTST có đáp án (Đề 1)

Câu 1:

Cho hàm số $y = f (x) = 2 x^{2} - 1.$ Khẳng định nào sau đây là đúng?

A. $f (- 1) = - 3.$

B. $f (1) = 1.$

C. $f (- 1) = - 1.$

D. $f (1) = 3.$

Xem đáp án

Chọn đáp án B

Câu 2:

Hàm số $y = a x + b$ là hàm số bậc nhất khi

A. $a = 0.$

B. $a < 0.$

C. $a > 0.$

D. $a \neq 0.$

Xem đáp án

Chọn đáp án D

Câu 3:

Đồ thị của hai hàm số y = x + 2 và y = x + 1

A. cắt nhau.

B. trùng nhau.

C. song song với nhau.

D. Cả A, B, C đều sai.

Xem đáp án

Chọn đáp án C

Câu 4:

Cho hình vẽ bên. Khẳng định nào sau đây là đúng về MN?

Cho hình vẽ bên. Khẳng định nào sau đây là đúng về MN? (ảnh 1)

A. là đường trung tuyến của $Δ A B C .$

B. là đường trung bình của $Δ A B C .$

C. là đường trung trực của $Δ A B C .$

D. là đường phân giác của

Δ A B C .

Xem đáp án

Chọn đáp án B

Câu 5:

Cho hình vẽ bên, biết $D E // A C .$ Tỉ số nào sau đây là đúng?

Cho hình vẽ bên, biết DE//AC. Tỉ số nào sau đây là đúng? (ảnh 1)

A. $\frac{B D}{A D} = \frac{B E}{E C} .$

B. $\frac{B D}{A D} = \frac{B E}{B C} .$

C. $\frac{D E}{A C} = \frac{B C}{B E} .$

D. $\frac{A D}{A B} = \frac{B C}{E C} .$

Xem đáp án

Chọn đáp án A

Câu 6:

Cho tam giác ABC có AB = 9cm, AC = 6cm Vẽ AD là đường phân giác của góc A Biết CD = 2cm độ dài đoạn thẳng DB là

A. 1,5 cm

B. 3 cm

C. 4,5 cm

D. 6 cm

Xem đáp án

Chọn đáp án B

Câu 7:

Trong giờ thực hành thí nghiệm, một học sinh thả một miếng chì có khối lượng 0,31 kg đang ở nhiệt độ $100 ° C$ vào 0,25kg nước đang ở nhiệt độ $58,5 ° C .$ Biết nhiệt dung riêng của nước là 4200 J/kg.K, nhiệt dung riêng của chì là 130 J/kg.K. gọi $t ° C$ là nhiệt độ khi đạt trạng thái cân bằng nhiệt, $Q_{n u o c}$ (J) là nhiệt lượng nước thu vào để tăng nhiệt độ từ $58,5 ° C$ lên $t ° C,$ $Q_{c h i}$ (J) là nhiệt lượng chì tỏa ra để giảm nhiệt độ từ $100 ° C$ xuống $t ° C.$

a) Biết công thức tính nhiệt lượng thu vào/ tỏa ra là: $Q = m \cdot c \cdot Δ t$ (J), trong đó m là khối lượng của vật (kg), c là nhiệt dung riêng của chất làm nên vật (J/kg.K) và $Δ t = t_{2} - t_{1}$ là độ tăng/giảm nhiệt độ của vật với $t_{1}$ là nhiệt độ ban đầu, $t_{2}$ là nhiệt độ cuối cùng. Viết công thức tính $Q_{c h i}$ và $Q_{n u o c}$ theo t

b) Khi có sự cân bằng nhiệt thì nhiệt độ của nước và chì là bao nhiêu (làm tròn kết quả đến hàng đơn vị)?

Xem đáp án

a) Nhiệt lượng chì tỏa ra để giảm nhiệt độ từ $100 ° C$ xuống $t ° C$ là:

$Q_{c h i} = 0,31 \cdot 130 \cdot (100 - t) = - 40,3 t + 4 030$ (J).

Nhiệt lượng nước thu vào để tăng nhiệt độ từ $58,5 ° C$ lên $t ° C$ là

(J).

b) Khi cân bằng nhiệt, nhiệt lượng tỏa ra bằng với nhiệt lượng thu vào nên ta có:

$Q_{n u o c} = Q_{c h i}$

Do đó $1 050 t - 61 425 = - 40,3 t + 4 030$

$1 090,3 t = 65 455$

$t \approx 60$

Vậy nhiệt độ của nước và chì khi đạt trạng thái cân bằng nhiệt là khoảng $60 ° C .$

Câu 8:

Cho hàm số $y = (m - 1) x + m$ (m là tham số $m \neq 1)$ có đồ thị là đường thẳng (d).

a) Tìm m để $(d) : y = (m - 1) x + m$ song song với $(d^{'}) : y = 2 x - 3.$

b) Vẽ (d) với m tìm được và vẽ (d') trên cùng mặt phẳng tọa độ Oxy.

c) Tìm m để đường thẳng $(d) : y = (m - 1) x + m$ và hai đường thẳng $y = x + 2; y = \frac{1}{2} x + 3$ đồng quy.

Xem đáp án

a) Với $m \neq 1,$ để đường thẳng $(d) : y = (m - 1) x + m$ song song với đường thẳng $(d^{'}) : y = 2 x - 3$ thì $m - 1 = 2$ và $m \neq - 3,$ tức là $m = 3$ (thỏa mãn $m \neq 1, m \neq - 3) .$

Vậy m = 3

b) ⦁ Với m = 3 ta có hàm số $y = 2 x + 3.$

Cho x = 0 ta có y = 3

Cho x = -1 ta có y = 1

Đồ thị hàm số $y = 2 x + 3$ là đường thẳng (d) đi qua hai điểm (0;3) và (-1;1)

⦁ Xét hàm số $y = 2 x - 3.$

Cho x = 0 ta có y = -3

Cho x = 1 ta có y = -1

Đồ thị hàm số $y = 2 x - 3$ là đường thẳng (d') đi qua hai điểm (0;-3) và (1;-1)

c) Gọi $A (x_{A}; y_{A})$ là giao điểm của hai đường thẳng $y = x + 2; y = \frac{1}{2} x + 3.$

Vì A thuộc đường thẳng y = x + 2 nên ta có $y_{A} = x_{A} + 2.$ Khi đó $A (x_{A}; x_{A} + 2) .$

Vì A thuộc đường thẳng $y = \frac{1}{2} x + 3$ nên ta có $x_{A} + 2 = \frac{1}{2} x_{A} + 3,$ suy ra $\frac{1}{2} x_{A} = 1,$ do đó $x_{A} = 2.$

Từ đó ta có $y_{A} = x_{A} + 2 = 2 + 2 = 4.$

Vì vậy ta được $A (2; 4) .$

Để ba đường thẳng $y = x + 2; y = \frac{1}{2} x + 3$ và $(d) : y = (m - 1) x + m$ đồng quy thì đường thẳng (d) phải đi qua giao điểm A(2;4) của hai đường thẳng $y = x + 2; y = \frac{1}{2} x + 3.$

Khi đó $x = 2, y = 4$ thỏa mãn hàm số $y = (m - 1) x + m,$ ta được:

$4 = (m - 1) \cdot 2 + m,$ suy ra $2 m - 2 + m = 4,$ do đó 3m = 6 nên m = 2 (thỏa mãn

Vậy m = 2.

Câu 9:

Cho tam giác ABC có $B C = 15 cm, C A = 18 cm$ và $A B = 12 cm .$ Gọi I và G lần lượt là tâm đường tròn nội tiếp và trọng tâm $Δ A B C .$

a) Tính độ dài các đoạn thẳng CD và BD.

b) Chứng minh $I G // B C .$

c) Tính độ dài đoạn thẳng IG.

Xem đáp án

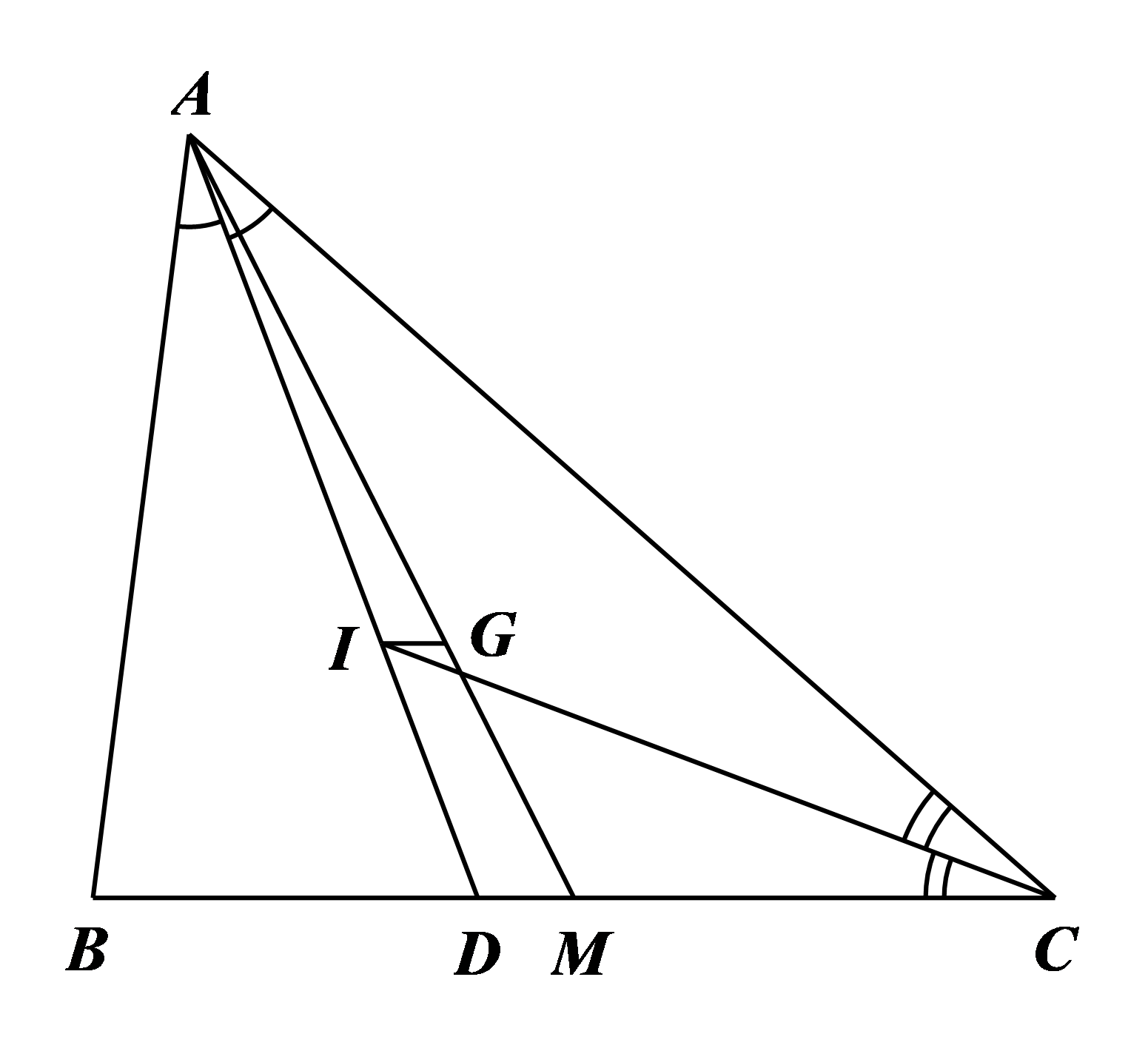
Cho tam giác ABC có BC = 15cm, C = 18 cm và AB = 12 cm Gọi I và G lần lượt là tâm đường tròn nội tiếp và trọng tâm tam giác ABC (ảnh 1)

a) Gọi AD là đường phân giác góc BAC $(D \in B C) .$

Xét $Δ A B C$ có AD là đường phân giác của $\hat{B A C}$ nên $\frac{A B}{A C} = \frac{D B}{D C},$ hay $\frac{D C}{A C} = \frac{D B}{A B} .$

Theo tính chất dãy tỉ số bằng nhau ta có:

\frac{D C}{A C} = \frac{D B}{A B} = \frac{D C + D B}{A C + A B} = \frac{B C}{A C + A B} = \frac{15}{18 + 12} = \frac{1}{2} .

Suy ra $C D = \frac{1}{2} A C = \frac{1}{2} \cdot 18 = 9 cm$ và $B D = \frac{1}{2} A B = \frac{1}{2} \cdot 12 = 6 cm .$

b) Xét $Δ A C D,$ có CI là đường phân giác của $\hat{A C D}$ nên $\frac{A G}{G M} = 2.$

Mặt khác, do G là trọng tâm của $Δ A B C$ nên $\frac{A G}{G M} = 2.$

Do đó $\frac{A I}{I D} = \frac{A G}{G M} = 2,$ theo định lí Thalès đảo ta có $I G // B C .$

c) Gọi M là trung điểm của BC. Khi đó $M B = M C = \frac{1}{2} B C = \frac{1}{2} \cdot 15 = 7,5 cm .$

Suy ra $D M = B M - B D = 7,5 - 6 = 1,5 cm .$

Xét $Δ A D M$ có $I G // B C,$ theo hệ quả định lí Thalès ta có $\frac{I G}{D M} = \frac{A G}{A M} = \frac{2}{3} .$

Suy ra $I G = \frac{2}{3} D M = \frac{2}{3} \cdot 1,5 = 1 cm .$

Câu 10:

Vì kèo mái tôn là một trong những bộ phận không thể thiếu trong cấu tạo mái nhà lợp tôn. Nó giúp chống đỡ và giảm trọng lực của những ảnh hưởng từ các yếu tố bên ngoài tác động vào (Hình a).

Vì kèo mái tôn là một trong những bộ phận không thể thiếu trong cấu tạo mái nhà lợp tôn. Nó giúp chống đỡ và giảm trọng lực của (ảnh 1)

Hình a

Vì kèo mái tôn là một trong những bộ phận không thể thiếu trong cấu tạo mái nhà lợp tôn. Nó giúp chống đỡ và giảm trọng lực của (ảnh 2)

Hình b

Một vì kèo mái tôn được vẽ lại như Hình b. Tính độ dài x của cây chống đứng bên và độ dài y của cánh kèo.

Xem đáp án

Đặt các điểm $A, B, C, D, E, M, N, P$ như hình vẽ trên.

⦁ Xét $Δ A M C$ có lần lượt là trung điểm của $A C, M C$ (do $E A = E C, P M = P C)$ nên EP là đường trung bình của $Δ A M C$

Do đó $E P = \frac{1}{2} A M = \frac{1}{2} \cdot 2,7 = 1,35 (m)$ (tính chất đường trung bình của tam giác).

Hay $x = 1,35 (m) .$

⦁ Ta có $M B = M N + N B$ và $M C = M P + P C$

Mà $M N = N B = M P = P C$ nên $M B = M C .$

Xét $Δ A B C$ có D, M lần lượt là trung điểm của $A B, B C$ (do $D B = D A, M B = M C)$ nên DM là đường trung bình của $Δ A B C .$

Do đó $D M = \frac{1}{2} A C$ (tính chất đường trung bình của tam giác).

Suy ra $A C = 2 D M = 2 \cdot 2,8 = 5,6 (m) .$ Hay $y = 5,6 (m) .$

Vậy độ dài của cây chống đứng bên và độ dài của của cánh kèo lần lượt là $x = 1,35 (m);$ $y = 5,6 (m) .$

Đề kiểm tra Giữa kì 2 Toán 8 CTST có đáp án

Đề kiểm tra Giữa kì 2 Toán 8 CTST có đáp án (Đề 1)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương