Đề kiểm tra giữa học kì 2 Toán lớp 7 CTST - Đề 02 có đáp án
-
313 lượt thi
-
18 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Thay tỉ số 1,25 : 3,45 bằng tỉ số giữa các số nguyên ta được
 Xem đáp án
Xem đáp án
Đáp án C
Ta có 1,25:3,45=1,253,45=2569.
Câu 2:
Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án A
Câu 3:
Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng
 Xem đáp án
Xem đáp án
Đáp án A
Hệ số tỉ lệ là: a = (–12) . 8 = –96.
Khi x = 3 thì y = –96 : 3 = –32.
Câu 4:
Cho hình vẽ sau:
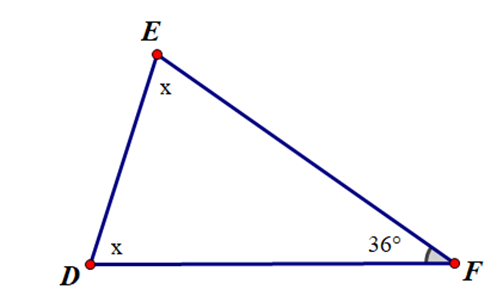
Số đo x là
 Xem đáp án
Xem đáp án
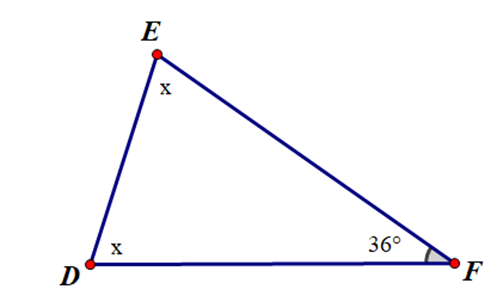
Áp dụng định lý về tổng số đo ba góc của tam giác ta có:
ˆD + ˆE + ˆF = 180°
Suy ra x + x + 36° = 180°
Hay 2x = 144°
Do đó x = 72°.
Câu 6:
Một tam giác cân có góc ở đáy bằng 40° thì số đo góc ở đỉnh là
 Xem đáp án
Xem đáp án
Đáp án D
Giả sử tam giác ABC cân tại A ta có: ˆB=ˆC= 40°.
Xét tam giác ABC có:
ˆA+ˆB+ˆC = 180° (tổng ba góc trong một tam giác).
Do đó ˆA = 180° − ˆB− ˆC = 180° − 40° − 40° = 100°.
Vậy số đo góc ở đỉnh là 100°.
Câu 8:
Điền vào chỗ trống sau: “Điểm … hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó”
 Xem đáp án
Xem đáp án
Đáp án B
Câu 9:
Tìm số hữu tỉ x trong tỉ lệ thức sau:
56:x=20:3;
 Xem đáp án
Xem đáp án
56:x=20:3
56x=203
x=56⋅320
x=5220
x=18
Vậy x=18.
Câu 10:
Tìm số hữu tỉ x trong tỉ lệ thức sau:
9x−19=53;
 Xem đáp án
Xem đáp án
9x−19=53
9x−1=5.93
9x – 1 = 15
9x = 16
x=169
Vậy x=169.
Câu 11:
Tìm số hữu tỉ x trong tỉ lệ thức sau:
x+1114−x=23.
 Xem đáp án
Xem đáp án
x+1114−x=23
3(x + 11) = 2(14 – x)
3x + 33 = 28 – 2x
3x + 2x = 28 – 33
5x = –5
x = –1
Vậy x = –1.
Câu 12:
Tìm giá trị a, b thỏa mãn 3a = 4b và b – a = 5.
 Xem đáp án
Xem đáp án
Từ 3a = 4b, ta suy ra a4=b3.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
a4=b3=b−a3−4=5−1=−5.
Suy ra a = (–5) . 4 = –20; b = (–5) . 3 = –15.
Do đó a = –20; b = –15.
Câu 13:
Cho a2=b3;b5=c4. Tìm a, b, c biết a + b + c = –74.
 Xem đáp án
Xem đáp án
Ta có:
⦁ a2=b3 suy ra a2.5=b3.5 hay a10=b15 (1)
⦁ b5=c4 suy ra b5.3=c4.3 hay b15=c12 (2)
Từ (1), (2) suy ra a10=b15=c12.
Áp dụng tính chất dãy tỉ sổ bằng nhau, ta có:
a10=b15=c12=a+b+c10+15+12=−7437=−2.
Suy ra a = (–2) . 10 = –20; b = (–2) . 15 = –30; c = (–2) . 12 = –24.
Do đó a = –20; b = –30; c = –24.
Câu 14:
Một ô tô đi từ A lúc 8 giờ. Đến 9 giờ một ô tô khác cũng đi xe từ A. Xe thứ nhất đến B lúc 2 giờ chiều. Xe thứ hai đến B sớm hơn xe thứ nhất nửa giờ. Tính vận tốc mỗi xe biết rằng vận tốc xe thứ hai lớn hơn vận tốc xe thứ nhất là 20 km/h.
 Xem đáp án
Xem đáp án
Trên cùng một quãng đường, vận tốc và thời gian tỉ lệ nghịch với nhau.
Gọi v1, t1 lần lượt là vận tốc và thời gian của xe I; v2, t2 lần lượt là vận tốc và thời gian của xe II.
Thời gian xe I đi hết đoạn đường AB là:
14 – 8 = 6 (giờ).
Thời gian xe II đi hết đoạn đường AB là:
(14 – 0,5) – 9 = 4,5 (giờ).
Ta có v1v2=t2t1=4,56=34 hay v13=v24.
Vì vận tốc xe thứ hai lớn hơn vận tốc xe thứ nhất là 20 km/h nên v2 – v1 = 20.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
v13=v24=v2−v14−3=201=20.
Suy ra v1 = 20 . 3 = 60; v2 = 20 . 4 = 80.
Vậy vận tốc của xe thứ nhất là 60 km/h, vận tốc của xe thứ hai là 80 km/h.
Câu 15:
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN).
Chứng minh rằng ∆BME = ∆CNF.
 Xem đáp án
Xem đáp án
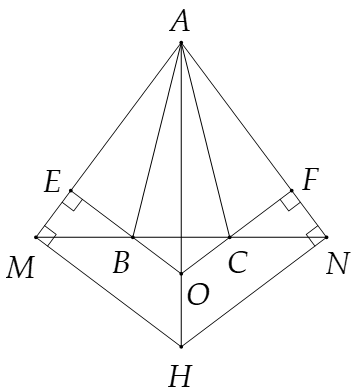
Vì ∆ABC cân tại A nên ^ABC=^ACB suy ra ^ABM=^ACN.
Xét ∆ABM và ∆CAN có:
AB = AC (vì ∆ABC cân tại A)
^ABM=^ACN (chứng minh trên)
BM = CN (giả thiết)
Do đó ∆ABM = ∆CAN (c.g.c).
Suy ra BM = CN (hai cạnh tương ứng); ^AMB=^ANC (hai góc tương ứng).
Xét ∆BME và ∆CNF có:
^BEM=^CFN=90∘
BM = CN (chứng minh trên)
^AMB=^ANC (chứng minh trên)
Do đó ∆BME = ∆CNF (cạnh huyền – góc nhọn).
Câu 16:
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN).
EB và FC kéo dài cắt nhau tại O. Chứng minh AO là tia phân giác của góc MAN
 Xem đáp án
Xem đáp án
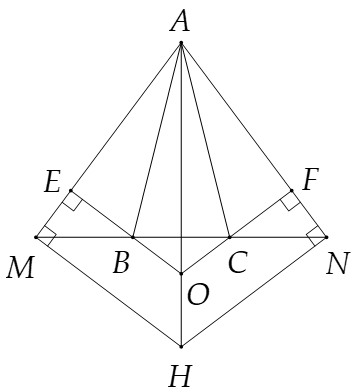
Từ câu b: ∆BME = ∆CNF suy ra ME = NF.
Mà AM = AN nên AE = AF.
Ta lại có ^EBM=^FCN suy ra ^OBC=^OCB.
Do đó ∆OBC cân tại O từ đó OB = OC suy ra OE = OF.
Xét ∆AEO và ∆AFO có:
AE = AF (chứng minh trên)
^AEO=^AFO=90∘
OE = OF (chứng minh trên)
Do đó ∆AEO = ∆AFO (c.g.c)
Suy ra ^OAE=^OAF (hai góc tương ứng).
Vậy AO là tia phân giác của góc MAN.
Câu 17:
ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN).
Qua M kẻ đường thẳng vuông góc với AM, qua N kẻ đường thẳng vuông góc với AN, chúng cắt nhau ở H. Chứng minh ba điểm A, O, H thẳng hàng.
 Xem đáp án
Xem đáp án
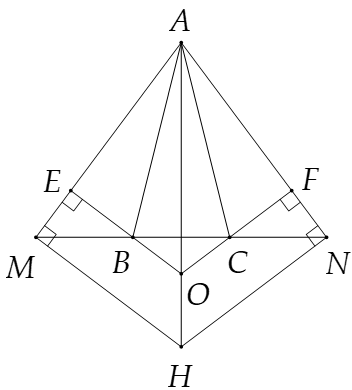
Xét ∆AMH và ∆ANH có:
^AMH=^ANH=90∘
Cạnh AH chung
AM = AN (chứng minh trên)
Do đó ∆AMH = ∆ANH (cạnh huyền – cạnh góc vuông)
Suy ra ^MAH=^NAH (hai góc tương ứng)
Suy ra AH là phân giác góc MAN.
Mặt khác AO là phân giác góc MAN nên AH và AO trùng nhau.
Do đó ba điểm A, O, H thẳng hàng.
Câu 18:
Cho tỉ lệ thức ab=cd. Chứng minh rằng a−2bb=c−2dd.
 Xem đáp án
Xem đáp án
Đặt ab=cd=k suy ra a = bk, c = dk.
Ta có a−2bb=bk−2bb=b(k−2)b=k−2;
c−2dd=dk−2dd=d(k−2)d=k−2.
Vậy a−2bb=c−2dd (đpcm).