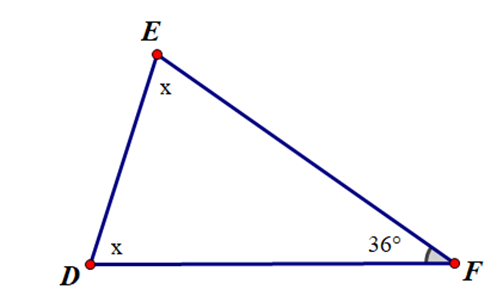
Câu hỏi:
02/02/2024 57
ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN).
Qua M kẻ đường thẳng vuông góc với AM, qua N kẻ đường thẳng vuông góc với AN, chúng cắt nhau ở H. Chứng minh ba điểm A, O, H thẳng hàng.
ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN).
Qua M kẻ đường thẳng vuông góc với AM, qua N kẻ đường thẳng vuông góc với AN, chúng cắt nhau ở H. Chứng minh ba điểm A, O, H thẳng hàng.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
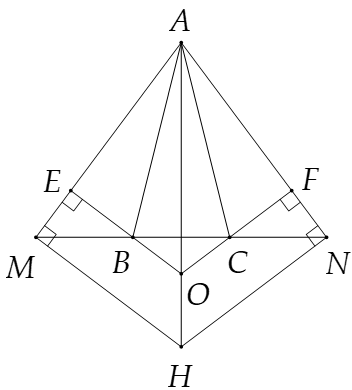
Xét ∆AMH và ∆ANH có:
\(\widehat {AMH} = \widehat {ANH} = 90^\circ \)
Cạnh AH chung
AM = AN (chứng minh trên)
Do đó ∆AMH = ∆ANH (cạnh huyền – cạnh góc vuông)
Suy ra \(\widehat {MAH} = \widehat {NAH}\) (hai góc tương ứng)
Suy ra AH là phân giác góc MAN.
Mặt khác AO là phân giác góc MAN nên AH và AO trùng nhau.
Do đó ba điểm A, O, H thẳng hàng.

Xét ∆AMH và ∆ANH có:
\(\widehat {AMH} = \widehat {ANH} = 90^\circ \)
Cạnh AH chung
AM = AN (chứng minh trên)
Do đó ∆AMH = ∆ANH (cạnh huyền – cạnh góc vuông)
Suy ra \(\widehat {MAH} = \widehat {NAH}\) (hai góc tương ứng)
Suy ra AH là phân giác góc MAN.
Mặt khác AO là phân giác góc MAN nên AH và AO trùng nhau.
Do đó ba điểm A, O, H thẳng hàng.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tìm số hữu tỉ x trong tỉ lệ thức sau:
\(\frac{{9x - 1}}{9} = \frac{5}{3}\);
Tìm số hữu tỉ x trong tỉ lệ thức sau:
\(\frac{{9x - 1}}{9} = \frac{5}{3}\);
Câu 4:
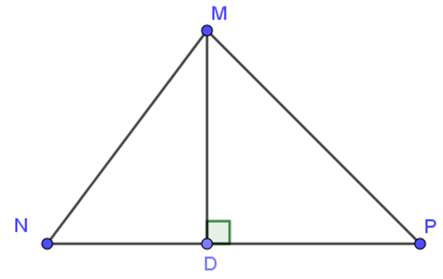
Cho tam giác MNP có: MN < MP, MD ⊥ NP. Khẳng định nào sau đây là đúng

Câu 5:
Tìm số hữu tỉ x trong tỉ lệ thức sau:
\(\frac{{x + 11}}{{14 - x}} = \frac{2}{3}\).
Tìm số hữu tỉ x trong tỉ lệ thức sau:
\(\frac{{x + 11}}{{14 - x}} = \frac{2}{3}\).
Câu 7:
Một ô tô đi từ A lúc 8 giờ. Đến 9 giờ một ô tô khác cũng đi xe từ A. Xe thứ nhất đến B lúc 2 giờ chiều. Xe thứ hai đến B sớm hơn xe thứ nhất nửa giờ. Tính vận tốc mỗi xe biết rằng vận tốc xe thứ hai lớn hơn vận tốc xe thứ nhất là 20 km/h.
Một ô tô đi từ A lúc 8 giờ. Đến 9 giờ một ô tô khác cũng đi xe từ A. Xe thứ nhất đến B lúc 2 giờ chiều. Xe thứ hai đến B sớm hơn xe thứ nhất nửa giờ. Tính vận tốc mỗi xe biết rằng vận tốc xe thứ hai lớn hơn vận tốc xe thứ nhất là 20 km/h.
Câu 10:
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN).
EB và FC kéo dài cắt nhau tại O. Chứng minh AO là tia phân giác của góc MAN
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN).
EB và FC kéo dài cắt nhau tại O. Chứng minh AO là tia phân giác của góc MAN
Câu 11:
Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng
Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng
Câu 12:
Cho tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\). Chứng minh rằng \(\frac{{a - 2b}}{b} = \frac{{c - 2d}}{d}\).
Cho tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\). Chứng minh rằng \(\frac{{a - 2b}}{b} = \frac{{c - 2d}}{d}\).
Câu 13:
Cho \(\frac{a}{2} = \frac{b}{3};\,\,\frac{b}{5} = \frac{c}{4}\). Tìm a, b, c biết a + b + c = –74.
Cho \(\frac{a}{2} = \frac{b}{3};\,\,\frac{b}{5} = \frac{c}{4}\). Tìm a, b, c biết a + b + c = –74.
Câu 14:
Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu?
Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu?
Câu 15:
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN).
Chứng minh rằng ∆BME = ∆CNF.
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN).
Chứng minh rằng ∆BME = ∆CNF.