21 câu hỏi trắc nghiệm thuộc Đề thi giữa kì 1 Toán 7 CTST có đáp án

Câu 1:

Điền kí hiệu thích hợp vào chỗ trống: 12,5 … ℚ:

A. Î;

B. Ï;

C. ⊂;

D. Một kí hiệu khác.

Xem đáp án

Chọn đáp án A

Câu 2:

Tìm số a biết số đối của a là $3 \frac{1}{4}$ .

A.

a = \frac{13}{4}

;

B.

a = \frac{- 4}{13}

;

C.

a = \frac{- 13}{4}

;

D.

a = \frac{4}{13}

.

Xem đáp án

Chọn đáp án C

Câu 3:

Rút gọn biểu thức $\frac{15^{8}}{9^{4}}$ ta được kết quả là:

A. 5⁵;

B. 5⁶;

C. 8⁵;

D. 5⁸.

Xem đáp án

Chọn đáp án D

Câu 4:

Những đồ vật sau có dạng hình gì?

A. Hình hộp chữ nhật;

B. Hình vuông;

C. Hình lập phương;

D. Hình chữ nhật.

Xem đáp án

Chọn đáp án B

Câu 5:

Cho hình lập phương ABCD.MNPQ có độ dài cạnh là 2 cm. Tính tổng diện tích các mặt của hình lập phương.

A. 8 cm²;

B. 12 cm²;

C. 24 cm²;

D. 20 cm².

Xem đáp án

Chọn đáp án C

Câu 6:

Chọn phát biểu đúng trong các phát biểu sau:

A. Hình lăng trụ tam giác có 4 mặt, 6 đỉnh;

B. Hình lăng trụ tam giác có 5 mặt, 6 đỉnh;

C. Hình lăng trụ tam giác có 6 mặt, 5 đỉnh;

D. Hình lăng trụ tam giác có 4 mặt, 4 đỉnh.

Xem đáp án

Chọn đáp án B

Câu 7:

Quan sát hình lập phương EFGH.MNPQ, biết MN = 3 cm, độ dài các cạnh EF, NF bằng bao nhiêu?

A. EF = NF = 3 cm;

B. EF = 3 cm; NF = 6cm;

C. EF = NF = 6 cm;

D. Các đáp án trên đều sai.

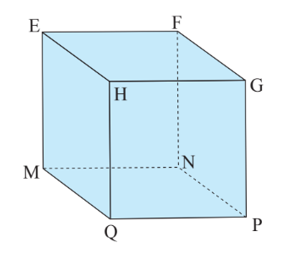
Xem đáp án

Chọn đáp án A

Câu 8:

Cho hình lăng trụ đứng tam giác có kích thước như hình vẽ.

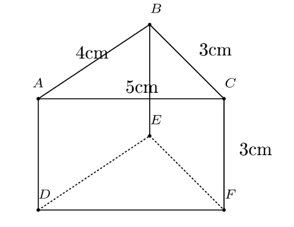
Diện tích xung quanh của hình lăng trụ đứng trên là:

A. 36 cm²;

B. 30 cm²;

C. 36 cm³;

D. 30 cm³.

Xem đáp án

Chọn đáp án C

Câu 9:

Cho các khẳng định sau:

(I). Hai góc đối đỉnh thì bằng nhau.

(II). Hai góc bằng nhau thì đối đỉnh.

(III). Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau.

Số khẳng định đúng là:

A. 1

B. 2

C. 3

D. Không có khẳng định nào đúng.

Xem đáp án

Chọn đáp án B

Câu 10:

Cho $\hat{x O y} = 30^{o}$ ; Oy là tia phân giác $\hat{x O y}$ . Khi đó $\hat{x O z}$ bằng:

A. 90°;

B. 120°;

C. 15°;

D. 60°.

Xem đáp án

Chọn đáp án D

Câu 11:

Số tự nhiên n thỏa mãn ${[{(0, 25)}^{4}]}^{3} = {(0, 25)}^{n}$ là:

A. 12;

B. 7

C. 1

D. 8

Xem đáp án

Chọn đáp án A

Câu 12:

Số nào dưới đây là giá trị của biểu thức $B = \frac{2}{11} - \frac{5}{13} + \frac{9}{11} - \frac{8}{13}$ ?

A. 2;

B. –1;

C. 1;

D. 0

Xem đáp án

Chọn đáp án D

Câu 13:

Thực hiện phép tính (tính hợp lý nếu có thể):

a) $- 0, 5 + \frac{2}{3} + \frac{1}{2}$ ;

Xem đáp án

a) $- 0, 5 + \frac{2}{3} + \frac{1}{2}$

$= \frac{- 1}{2} + \frac{2}{3} + \frac{1}{2}$

$= (\frac{- 1}{2} + \frac{1}{2}) + \frac{2}{3}$

$= 0 + \frac{2}{3} = \frac{2}{3}$ .

Câu 14:

b) ${(1 - \frac{1}{2} + \frac{1}{4})}^{2} . (2 - \frac{3}{2})$

Xem đáp án

b) ${(1 - \frac{1}{2} + \frac{1}{4})}^{2} . (2 - \frac{3}{2})$

$= {(\frac{4}{4} - \frac{2}{4} + \frac{1}{4})}^{2} . (\frac{4}{2} - \frac{3}{2})$

$= {(\frac{3}{4})}^{2} . \frac{1}{2} = \frac{9}{16} . \frac{1}{2} = \frac{9}{32}$ .

Câu 15:

c) $1, 2 . \frac{15}{4} + \frac{16}{7} . \frac{- 85}{8} - 1, 2 . 5 \frac{3}{4} - \frac{16}{7} . \frac{- 71}{8}$

Xem đáp án

c) $1, 2 . \frac{15}{4} + \frac{16}{7} . \frac{- 85}{8} - 1, 2 . 5 \frac{3}{4} - \frac{16}{7} . \frac{- 71}{8}$

$= (\frac{6}{5} . \frac{15}{4} - \frac{6}{5} . \frac{23}{4}) + (\frac{16}{7} . \frac{- 85}{8} - \frac{16}{7} . \frac{- 71}{8})$

$= \frac{6}{5} . (\frac{15}{4} - \frac{23}{4}) + \frac{16}{7} . (\frac{- 85}{8} - \frac{- 71}{8})$

$= \frac{6}{5} . (\frac{- 8}{4}) + \frac{16}{7} . (\frac{- 14}{8})$

$= \frac{6}{5} . (- 2) + \frac{16}{7} . (\frac{- 7}{4})$

$= \frac{- 12}{5} + (- 4)$

$= \frac{- 12}{5} + \frac{- 20}{5} = \frac{- 32}{5}$ .

Câu 16:

Tìm x biết:

a) $\frac{16}{5} - x = \frac{4}{5} - \frac{3}{10}$ ;

Xem đáp án

a) $\frac{16}{5} - x = \frac{4}{5} - \frac{3}{10}$

$\frac{16}{5} - x = \frac{8}{10} - \frac{3}{10}$

$\frac{16}{5} - x = \frac{5}{10}$

$\frac{16}{5} - x = \frac{1}{2}$

$x = \frac{16}{5} - \frac{1}{2}$

$x = \frac{32}{10} - \frac{5}{10}$

$x = \frac{27}{10}$

Vậy $x = \frac{27}{10}$ .

Câu 17:

b) (2x – 8)^{2 022} = (3 – 4x)^{2 022}

Xem đáp án

b) (2x – 8)^{2 022} = (3 – 4x)^{2 022}

2x – 8 = 3 – 4x.

2x + 4x = 3 + 8.

6x = 11.

$x = \frac{11}{6}$ .

Vậy $x = \frac{11}{6}$ .

Câu 18:

Một nhà kho có dạng hình lăng trụ đứng, đáy là hình thang vuông. Chiều cao của hình lăng trụ đứng (là chiều dài của nhà kho) bằng 6 m. Đường cao của đáy (là chiều rộng của nhà kho) bằng 5 m. Các cạnh đáy của hình thang vuông dài 3 m và 4 m. Tính thể tích của nhà kho.

Xem đáp án

Hướng dẫn giải

Gọi nhà kho có dạng hình lăng trụ đứng ABCD.A’B’C’D’.

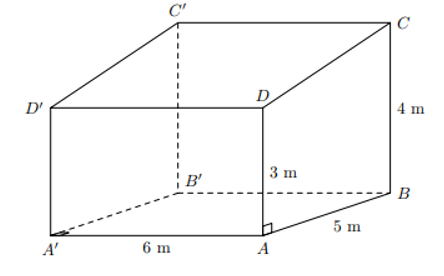
Một nhà kho có dạng hình lăng trụ đứng, đáy là hình thang vuông. Chiều cao của hình lăng (ảnh 1)

Diện tích đáy hình lăng trụ là:

$S_{A B C D} = \frac{1}{2} . (3 + 4) . 5 = 17, 5$ (cm²)

Thể tích nhà kho là:

V_kho = S_ABCD . AA’ = 17,5 . 6 = 105 (cm³)

Vậy thể tích nhà kho là 105 cm³.

Câu 19:

Một phòng học hình hộp chữ nhật có chiều dài 8 m, chiều rộng 5 m, chiều cao 4 m. Người ta quét vôi bên trong lớp học, kể cả trần. Biết tổng diện tích các cửa ra vào và cửa sổ là 10 m². Tính diện tích phải quét vôi.

Xem đáp án

Hướng dẫn giải

Gọi căn phòng là hình hộp chữ nhật ABCD.A’B’C’D’.

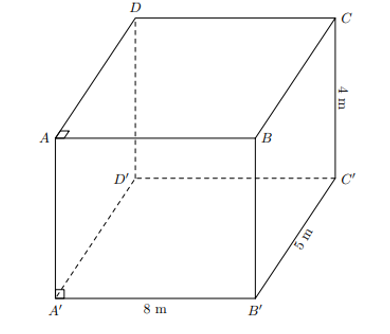
Một phòng học hình hộp chữ nhật có chiều dài 8 m, chiều rộng 5 m, chiều cao 4 m. (ảnh 1)

Chu vi căn phòng hình chữ nhật là:

2 . (8 + 5) = 26 (m)

Diện tích xung quanh của căn phòng là:

S_xq = 26 . 4 = 104 (m²)

Diện tích trần của căn phòng là:

S_trần = 8 . 5 = 40 (m²)

Diện tích phải quét vôi là:

S = S_xq + S_trần – 10 = 104 + 40 – 10 = 134 (m²).

Vậy diện tích phải quét vôi là 134 m².

Câu 20:

Cho góc bẹt $\hat{a O b}$ . Gọi Oc là tia phân giác của $\hat{a O b}$ ; Ox là phân giác của $\hat{a O c}$ ; Oy là phân giác của $\hat{c O b}$ . Tính số đo $\hat{x O y}$ .

Xem đáp án

Hướng dẫn giải

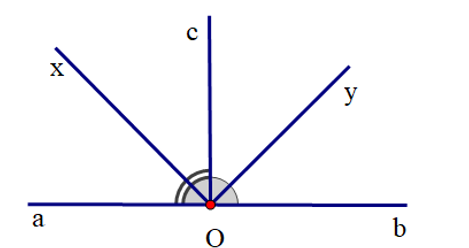
Cho góc bẹt aOb. Gọi Oc là tia phân giác của góc aOb ; Ox là phân giác của góc aOc (ảnh 1)

Vì Oc là tia phân giác của $\hat{a O b}$ nên $\hat{a O c} = \hat{c O b} = \frac{1}{2} \hat{a O b}$ .

Suy ra $\hat{a O c} = \hat{c O b} = \frac{1}{2} {.180}^{o} = 90^{o}$ (vì $\hat{a O b}$ là góc bẹt)

Vì Ox là phân giác của $\hat{a O c}$ nên:

$\hat{x O c} = \frac{1}{2} \hat{a O c} = \frac{1}{2} {.90}^{o} = 45^{o}$ .

Vì Oy là phân giác của $\hat{c O b}$ nên:

$\hat{c O y} = \frac{1}{2} \hat{c O b} = \frac{1}{2} {.90}^{o} = 45^{o}$ .

Ta có tia Oc nằm giữa hai tia Ox và Oy nên:

$\hat{x O y} = \hat{x O c} + \hat{c O y} = 45^{o} + 45^{o} = 90^{o}$ .

Vậy $\hat{x O y} = 90^{o}$ .

Câu 21:

Tính giá trị nhỏ nhất của biểu thức M = (x – 5)² + 7.

Xem đáp án

Hướng dẫn giải

Ta có (x – 5)² ≥ 0 nên (x – 5)² + 7 ≥ 7.

Dấu "=" xảy ra khi (x – 5)² = 0

Suy ra x – 5 = 0

Do đó x = 5.

Vậy giá trị nhỏ nhất của biểu thức M bằng 7 khi x = 5.

Đề thi giữa kì 1 Toán 7 CTST có đáp án

Đề thi giữa kì 1 Toán 7 CTST có đáp án - Đề 1

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương