16 câu hỏi trắc nghiệm thuộc Đề kiểm tra Cuối kì 1 Toán 8 CTST có đáp án (Đề 2)

Câu 1:

Cho các biểu thức $- 5 x y^{2} + x y z; - \frac{1}{4} x y; x^{2} - 3 x + 5; \frac{2}{7} x y + 3 y$ , có bao nhiêu đa thức nhiều biến?

A. 4.

B. 3.

C. 2.

D. 1.

Xem đáp án

Chọn đáp án B

Câu 2:

Phân tích đa thức $(x^{2} + 4 x + 4) - (x + 2)$ thành nhân tử ta được

A. $x (x + 3)$

B. $x (x + 2)$

C. $(x + 2) (x + 1)$

D. $(x + 2) (x + 3)$

Xem đáp án

Chọn đáp án C

Câu 3:

Biểu thức nào sau đây không phải là phân thức đại số?

A. $\frac{2}{x} .$

B. $\frac{x}{x + 1} .$

C. $x^{2} - 4.$

D. $\frac{x + 1}{0} .$

Xem đáp án

Chọn đáp án D

Câu 4:

Số đo mỗi góc ở đỉnh của đáy hình chóp tam giác đều là

A. $60 ° .$

B. $90 ° .$

C. $120 ° .$

D. $180 ° .$

Xem đáp án

Chọn đáp án A

Câu 5:

Một hình chóp đều và một hình lăng trụ đứng có diện tích đáy bằng nhau. Chiều cao của hình chóp đều gấp đôi chiều cao của hình lăng trụ đứng. Thể tích của hình chóp đều là

A. $V = \frac{1}{3} S h .$

B. $V = S h .$

C. $V = \frac{2}{3} S h .$

D. $V = 2 S h .$

Xem đáp án

Chọn đáp án C

Câu 6:

Cho tứ giác ABCD có $\hat{A} + \hat{B} = 220 ° .$ Các tia phân giác của các góc C và D cắt nhau tại I Khi đó số đo $\hat{C I D}$ là

A. $\hat{C I D} = 110 ° .$

B. $\hat{C I D} = 120 ° .$

C. $\hat{C I D} = 140 ° .$

D. $\hat{C I D} = 150 ° .$

Xem đáp án

Chọn đáp án A

Câu 7:

Chọn nhận định sai.

Tứ giác nào có hai đường chéo bằng nhau?

A. Hình thoi.

B. Hình vuông.

C. Hình chữ nhật.

D. Hình thang cân.

Xem đáp án

Chọn đáp án A

Câu 8:

Nhiệt độ trung bình các tháng trong năm của một quốc gia được biểu diễn trong bảng sau:

Tháng	1	2	3	4	5	6	7	8	9	10	11	12
Nhiệt độ (độ C)	2	3	5	15	20	30	29	27	20	15	12	7

Biểu đồ thích hợp để biểu diễn dữ liệu trong bảng trên là

A. Biểu đồ hình quạt tròn.

B. Biểu đồ đoạn thẳng.

C. Biểu đồ cột tranh.

D. Không thể biểu diễn được.

Xem đáp án

Chọn đáp án B

Câu 9:

Tìm x biết:

a) $3 {(x - 1)}^{2} - 3 x (x - 5) = 0.$ b) ${(x + 3)}^{2} - 5 x - 15 = 0.$

Xem đáp án

a) $3 {(x - 1)}^{2} - 3 x (x - 5) = 0$

$3 (x^{2} - 2 x + 1) - (3 x^{2} - 15 x) = 0$

$3 x^{2} - 6 x + 3 - 3 x^{2} + 15 x = 0$

$(3 x^{2} - 3 x^{2}) + (- 6 x + 15 x) + 3 = 0$

$9 x = - 3$

$x = - \frac{1}{3} .$

Vậy $x = - \frac{1}{3} .$

b) ${(x + 3)}^{2} - 5 x - 15 = 0$

${(x + 3)}^{2} - (5 x - 15) = 0$

${(x + 3)}^{2} - 5 (x + 3) = 0$

$(x + 3) (x + 3 - 5) = 0$

$(x + 3) (x - 2) = 0$

Suy ra x + 3 = 0 hoặc x - 2 = 0

x = -3 hoặc x = 2

Vậy $x \in \{- 3; 2\}$

Câu 10:

a) Tìm điều kiện xác định của biểu thức A

Xem đáp án

a) Với mọi x ta có:

⦁ $2 x^{2} + 8 = 2 (x^{2} + 4) .$

Mà $x^{2} \geq 0$ nên $x^{2} + 4 \geq 4 > 0$ hay $2 (x^{2} + 4) > 0.$

⦁ $x^{3} - 2 x^{2} + 4 x - 8 = (x^{3} - 2 x^{2}) + (4 x - 8)$

$= x^{2} (x - 2) + 4 (x - 2) = (x - 2) (x^{2} + 4)$ .

Khi đó biểu thức A xác định khi và chỉ khi $x - 2 \neq 0$ và $x \neq 0$ hay $x \neq 2$ và $x \neq 0$

Câu 11:

b) Rút gọn biểu thức A

Xem đáp án

b) Với $x \neq 2$ và $x \neq 0$ ta có:

$A = (\frac{2 x - x^{2}}{2 x^{2} + 8} - \frac{2 x^{2}}{x^{3} - 2 x^{2} + 4 x - 8}) \cdot (\frac{2}{x^{2}} - \frac{x - 1}{x})$

$= [\frac{2 x - x^{2}}{2 (x^{2} + 4)} - \frac{2 x^{2}}{(x^{2} + 4) (x - 2)}] \cdot [\frac{2}{x^{2}} - \frac{x (x - 1)}{x^{2}}]$

$= \frac{(2 x - x^{2}) (x - 2) - 2 x^{2} \cdot 2}{2 (x^{2} + 4) (x - 2)} \cdot \frac{2 - x^{2} + x}{x^{2}}$

$= \frac{2 x^{2} - 4 x - x^{3} + 2 x^{2} - 4 x^{2}}{2 (x^{2} + 4) (x - 2)} \cdot \frac{- x^{2} + 2 x - x + 2}{x^{2}}$

$= \frac{- 4 x - x^{3}}{2 (x^{2} + 4) (x - 2)} \cdot \frac{- x (x - 2) - (x - 2)}{x^{2}}$

$= \frac{- x (x^{2} + 4)}{2 (x^{2} + 4) (x - 2)} \cdot \frac{- (x - 2) (x + 1)}{x^{2}}$ $= \frac{x + 1}{2 x} .$

Vậy với $x \neq 2$ và $x \neq 0$ thì $A = \frac{x + 2}{2 x} .$

Câu 12:

c) Tính giá trị của biểu thức A khi x = 2024

Xem đáp án

c) Thay x = 2024 (thỏa mãn điều kiện) vào biểu thức $A = \frac{x + 2}{2 x},$ ta được:

$A = \frac{2 024 + 2}{2 \cdot 2 024} = \frac{2 026}{2 \cdot 2 024} = \frac{1 013}{2 024} .$

Vậy với x = 2024 thì $A = \frac{1 013}{2 024} .$

Câu 13:

Chị Lan đã ghi lại khối lượng bán được của mỗi loại mà sạp hoa quả của chị bán được trong ngày và biểu diễn trong biểu đồ dưới đây:

Chị Lan đã ghi lại khối lượng bán được của mỗi loại mà sạp hoa quả của chị bán được trong ngày và biểu diễn trong biểu đồ dưới đây (ảnh 1)

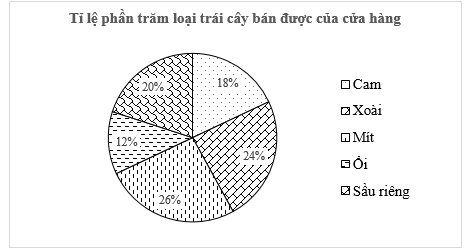
a) Chị Lan đã thu thập dữ liệu được biểu diễn trên biểu đồ bằng phương pháp thu thập trực tiếp hay gián tiếp?

b) Hãy chuyển đổi dữ liệu từ biểu đồ trên sang dạng bảng thống kê theo mẫu sau:

Loại trái cây	Tỉ lệ phần trăm
Cam	?
Xoài	?
Mít	?
Ổi	?
Sầu riêng	?

c) Cho biết chị Lan bán được tổng cộng 200 kg trái cây trong ngày hôm đó. Hãy tính số kilôgam sầu riêng mà sạp hoa quả của chị Lan đã bán được trong ngày ấy.

Xem đáp án

a) Chị Lan đã ghi lại, thống kê và biểu diễn dữ liệu trên biểu đồ đã cho nên ta kết luận chị đã thu thập dữ liệu được biểu diễn trên biểu đồ bằng phương pháp thu thập trực tiếp.

b) Từ biểu đồ hình quạt tròn, ta hoàn thành được bảng thống kê sau:

Loại trái cây	Tỉ lệ phần trăm
Cam	18%
Xoài	24%
Mít	26%
Ổi	12%
Sầu riêng	20%

c) Số kilôgam sầu riêng mà sạp hoa quả của chị Lan đã bán được trong ngày hôm đó là: $200 \cdot 20 % = 40 (kg) .$

Câu 14:

Bạn Hoa dự định làm 4 hộp quà có dạng hình chóp tứ giác đều như hình bên có cạnh đáy 6 cm, chiều cao của mặt bên xuất phát từ đỉnh là 4 cm. Tính diện tích giấy mà bạn Hoa cần dùng để làm 4 hộp quà đó.

Bạn Hoa dự định làm 4 hộp quà có dạng hình chóp tứ giác đều như hình bên có cạnh đáy 6 cm, chiều cao của mặt bên (ảnh 1)

Xem đáp án

Diện tích xung quanh của một hộp quà là:

$S_{x q} = \frac{1}{2} \cdot (4 \cdot 6) \cdot 4 = 48 ({cm}^{2}) .$

Diện tích toàn phần của một hộp quà là

$S_{t p} = S_{x q} + S_{đ á y} = 48 + 6^{2} = 84 ({cm}^{2}) .$

Để làm 4 hộp quà bạn Hoa cần dùng diện tích giấy là:

$4 \cdot 84 = 336 ({cm}^{2}) .$

Vậy diện tích giấy mà bạn Hoa cần dùng để làm 4 hộp quà là $336 {cm}^{2} .$

Câu 15:

Cho hình vuông ABCD. Lấy điểm M thuộc đường chéo BD. Kẻ ME vuông góc với AB tại E, MF vuông góc với AD tại F.

a) Tứ giác AEMF là hình gì? Vì sao?

b) Xác định vị trí của điểm M trên đường chéo BD để diện tích của tứ giác AEMF lớn nhất.

Xem đáp án

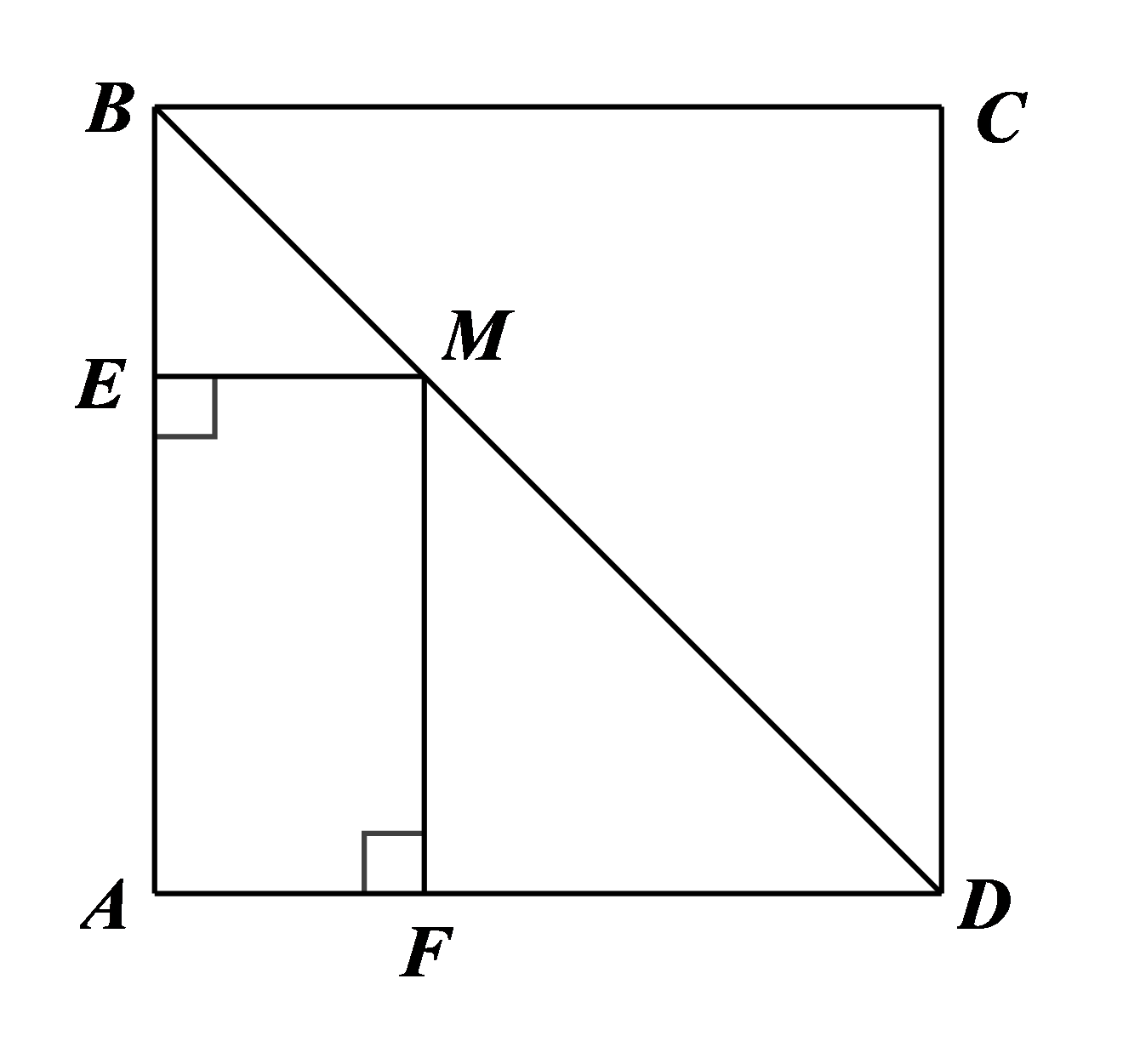
Cho hình vuông ABCD. Lấy điểm M thuộc đường chéo BD. Kẻ ME vuông góc với AB tại E, MF vuông góc với AD tại F. (ảnh 1)

a) Do $M E ⊥ A B$ tại E nên $\hat{M E A} = 90 ° .$

Do $M F ⊥ A D$ tại F nên $\hat{M F A} = 90 ° .$

Do ABCD là hình vuông nên $\hat{E A F} = 90 ° .$

Tứ giác AEMF có $\hat{M F A} = \hat{E A F} = \hat{A E M} = 90 °$ nên AEMF là hình chữ nhật.

b) Do ABCD là hình vuông nên BD là đường phân giác của góc $\hat{A B C}$ .

Do đó $\hat{A B D} = 45 °$ suy ra $Δ B E M$ vuông cân tại E

Nên $B E = M E .$

Do AEMF là hình chữ nhật nên ME = AF nên BE = AF

Chu vi của hình chữ nhật AEMF là:

$2 (A E + A F) = 2 (A E + B E) = 2 A B .$

Mà AB không đổi nên chu vi của hình chữ nhật AEMF không đổi.

Do đó, diện tích của tứ giác AEMF lớn nhất khi AEMF là hình vuông.

Suy ra $M E = M F .$

Khi đó $Δ B E M = Δ D F M$ (cạnh góc vuông – góc nhọn kề).

Suy ra BM = DM hay M là trung điểm của BC

Vậy với M là trung điểm của BC thì diện tích của tứ giác AEMF lớn nhất.

Câu 16:

Cho a + b + c = 0; x + y + z = 0 và = $\frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0.$

Chứng minh rằng: $a x^{2} + b y^{2} + c z^{2} = 0.$

Xem đáp án

Do $x + y + z = 0$ nên $\{\begin{cases} x = - (y + z) \\ y = - (x + z) \\ z = - (x + y) \end{cases}$ , suy ra $\{\begin{cases} x^{2} = {(y + z)}^{2} \\ y^{2} = {(x + z)}^{2} \\ z^{2} = {(x + y)}^{2} \end{cases} .$

Do $a + b + c = 0$ nên $\{\begin{cases} b + c = - a \\ c + a = - b \\ a + b = - c \end{cases} .$

Do $\frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0$ nên $\frac{a y z + b x z + c x y}{x y z} = 0$ suy ra $b x z + c x y + a y z = 0$ .

Ta có: $a x^{2} + b y^{2} + c z^{2} = a {(y + z)}^{2} + b {(x + z)}^{2} + c {(x + y)}^{2}$

$= a y^{2} + 2 a y z + a z^{2} + b x^{2} + 2 b x z + b z^{2} + c x^{2} + 2 c x y + c y^{2}$

$= (b + c) x^{2} + (a + c) y^{2} + (a + b) z^{2} + 2 (b x z + c x y + a y z)$

$= (b + c) x^{2} + (a + c) y^{2} + (a + b) z^{2}$

$= (- a) x^{2} + (- b) y^{2} + (- c) z^{2}$

Do đó $2 (a x^{2} + b y^{2} + c z^{2}) = 0$ nên $a x^{2} + b y^{2} + c z^{2} = 0.$

Vậy $a x^{2} + b y^{2} + c z^{2} = 0.$

Đề kiểm tra Cuối kì 1 Toán 8 CTST có đáp án

Đề kiểm tra Cuối kì 1 Toán 8 CTST có đáp án (Đề 2)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương