14 câu hỏi trắc nghiệm thuộc Dạng 2: Biểu thức tọa độ của phép tịnh tiến có đáp án

Câu 1:

\vec{v} = (- 2; 3)

. Hãy tìm ảnh của các điểm

A (1; - 1), B (4; 3)

qua phép tịnh tiến theo vectơ

\vec{v}

.

Xem đáp án

Hướng dẫn giải

Biểu thức tọa độ của phép tịnh tiến $T_{\vec{v}}$ là $\{\begin{cases} x' = x - 2 \\ y' = y + 3 \end{cases}$

Ta có điểm $A (1; - 1)$ .

$\begin{array}{l} A' (x'; y') = T_{\vec{v}} (A) \Rightarrow \{\begin{cases} x' = 1 + (- 2) \\ y' = - 1 + 3 \end{cases} \\ \Leftrightarrow \{\begin{cases} x' = - 1 \\ y' = 2 \end{cases} \Rightarrow A' (- 1; 2) \end{array}$

Tương tự ta có ảnh của B là điểm

B' (2; 6)

Câu 2:

Trong mặt phẳng tọa độ Oxy, cho $\vec{v} = (1; - 3)$ và đường thẳng d có phương trình $2 x - 3 y + 5 = 0$ . Viết phương trình đường thẳng d’ là ảnh của d qua phép tịnh tiến .

Xem đáp án

Hướng dẫn giải

Cách 1: Sử dụng biểu thức tọa độ của phép tịnh tiến.

Lấy điểm tùy ý thuộc d, ta có: $2 x - 3 y + 5 = 0 (*)$

Gọi $M' (x'; y') = T_{\vec{v}} (M) \Rightarrow \{\begin{cases} x' = x + 1 \\ y' = y - 3 \end{cases} \Leftrightarrow \{\begin{cases} x = x' - 1 \\ y = y' + 3 \end{cases}$

Thay vào (*) ta được phương trình: $2 (x' - 1) - 3 (y' + 3) + 5 = 0 \Leftrightarrow 2 x' - 3 y' - 6 = 0$

Vậy ảnh của d là đường thẳng $d' : 2 x - 3 y - 6 = 0$ .

Cách 2: Sử dụng tính chất của phép tịnh tiến

Do $d' = T_{\vec{v}} (d)$ nên d’ song song hoặc trùng với d, vì vậy phương trình đường thẳng d’ có dạng $2 x - 3 y + c = 0 (* *)$

Lấy điểm $M (- 1; 1) \in d$ . Khi đó $M' = T_{\vec{v}} (M) = (- 1 + 1; 1 - 3) = (0; - 2)$

Do $M' \in d'$ nên $2.0 - 3. (- 2) + c = 0 \Leftrightarrow c = - 6$

Vậy ảnh của d là đường thẳng $d' : 2 x - 3 y - 6 = 0$

Câu 3:

Trong mặt phẳng Oxy, cho đường tròn (C) có phương trình

x^{2} + y^{2} + 2 x - 4 y - 4 = 0

. Tìm ảnh của (C) qua phép tịnh tiến theo vectơ

\vec{v} = (2; - 3)

.

Xem đáp án

Sử dụng biểu thức tọa độ.

Lấy điểm $M (x; y)$ tùy ý thuộc đường tròn (C) , ta có: $x^{2} + y^{2} + 2 x - 4 y - 4 = 0 (*)$

Gọi $M' (x'; y') = T_{\vec{v}} (M) \Rightarrow \{\begin{cases} x' = x + 2 \\ y' = y - 3 \end{cases} \Leftrightarrow \{\begin{cases} x = x' - 2 \\ y = y' + 3 \end{cases}$

Thay vào phương trình (*), ta được: $\begin{array}{l} {(x' - 2)}^{2} + {(y' + 3)}^{2} + 2 (x' - 2) - 4 (y' + 3) - 4 = 0 \\ \Leftrightarrow x'^{2} + y'^{2} - 2 x' + 2 y' - 7 = 0 \end{array}$

Vậy ảnh của (C) là đường tròn $(C') : x^{2} + y^{2} - 2 x + 2 y - 7 = 0$

Câu 4:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng $d : 3 x + y - 9 = 0$ . Tìm phép tịnh tiến theo vectơ $\vec{v}$ có giá song song với Oy biến d thành d’ đi qua điểm $A (1; 1)$ .

Xem đáp án

Hướng dẫn giải

$\vec{v}$ có giá song song với Oy nên $\vec{v} = (0; k) (k \neq 0)$

Lấy $M (x; y) \in d \Rightarrow 3 x + y - 9 = 0 (*)$

Gọi $M' (x'; y') = T_{\vec{v}} (M) \Rightarrow \{\begin{cases} x' = x \\ y' = y + k \end{cases} \Leftrightarrow \{\begin{cases} x = x' \\ y = y' - k \end{cases}$

Thay vào (*), ta có $3 x' + y' - k - 9 = 0$ hay $T_{\vec{v}} (d) = d' : 3 x + y - k - 9 = 0$

Mà d’ đi qua $A (1; 1)$ nên $k = - 5$

Vậy $\vec{v} = (0; - 5)$

Câu 5:

Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng $d : 2 x - 3 y + 3 = 0$ và $d' : 2 x - 3 y - 5 = 0$ . Tìm tọa độ $\vec{v}$ có phương vuông góc với d để $T_{\vec{v}} (d) = d'$ .

Xem đáp án

Hướng dẫn giải

Đặt $\vec{v} = (a; b)$ , lấy điểm $M (0; 1) \in d$ .

Giả sử $M' (x'; y') = T_{\vec{v}} (M)$ .

Ta có $\{\begin{cases} x' = a \\ y' = 1 + b \end{cases}$ thay vào d’ ta được phương trình $2 a - 3 b = 8$ .

Vectơ pháp tuyến của đường thẳng d là $\vec{n} = (2; - 3)$

Suy ra vectơ chỉ phương của d là $\vec{u} = (3; 2)$

Do $\vec{v} ⊥ \vec{u}$ nên $\vec{v} . \vec{u} = 0 \Rightarrow 3 a + 2 b = 0$

Ta có hệ phương trình $\{\begin{cases} 2 a - 3 b = 8 \\ 3 a + 2 b = 0 \end{cases} \Leftrightarrow \{\begin{cases} a = \frac{16}{13} \\ b = - \frac{24}{13} \end{cases}$

Vậy $\vec{v} = (\frac{16}{13}; - \frac{24}{13})$

Câu 6:

Trong mặt phẳng tọa độ Oxy, cho điểm $A (3; - 3)$ Ảnh của điểm A qua phép tịnh tiến theo vectơ $\vec{v} = (- 1; 3)$ là:

A. $A' (2; - 6)$

B. $A' (2; 0)$

C. $A' (4; 0)$

D. $A' (- 2; 0)$

Xem đáp án

Ta có: $T_{\vec{v}} (A) = A' (x_{A}; y_{A}) \Leftrightarrow \vec{A A'} = \vec{v} \Leftrightarrow \{\begin{cases} x_{A'} = x_{A} + x_{\vec{v}} \\ y_{A'} = y_{A} + y_{\vec{v}} \end{cases} \Rightarrow \{\begin{cases} x_{A'} = 3 - 1 = 2 \\ y_{A'} = - 3 + 3 = 0 \end{cases} \Rightarrow A' (2; 0)$

Câu 7:

Cho ba điểm $M (2; 3); N (- 4; 1); P (6; 5)$ . Ảnh của N qua phép tịnh tiến theo vectơ $\vec{M P}$ là:

A. $N' (0; 3)$

B. $N' (- 3; 7)$

C. $N' (3; 7)$

D. $N' (3; 0)$

Xem đáp án

Ta có $\vec{M P} = (4; 2)$

Gọi $N' (x'; y')$ là ảnh của $N (- 4; 1)$ qua phép tịnh tiến theo vectơ $\vec{M P}$ .

Áp dụng biểu thức tọa độ của phép tịnh tiến $\{\begin{cases} x' = x + a \\ y' = y + b \end{cases}$ , ta có: $\{\begin{cases} x' = - 4 + 4 \\ y' = 1 + 2 \end{cases} \Leftrightarrow \{\begin{cases} x = 0 \\ y = 3 \end{cases}$

Vậy $N' (0; 3)$

Câu 8:

Trong mặt phẳng tọa độ Oxy, cho hai điểm $M (0; 2), N (- 2; 1)$ và vectơ $\vec{v} (1; 2)$ . Phép tịnh tiến theo vectơ $\vec{v}$ biến M, N thành hai điểm M’, N’ tương ứng. Tính độ dài M’N’.

A. $M' N' = \sqrt{5}$

B. $M' N' = \sqrt{7}$

C. $M' N' = 1$

D. $M' N' = 3$

Xem đáp án

Ta có: $\{\begin{cases} T_{\vec{v}} (M) = M' \\ T_{\vec{v}} (N) = N' \end{cases} \Rightarrow M N = M' N' = \sqrt{{(- 2 - 0)}^{2} + {(1 - 2)}^{2}} = \sqrt{5}$

Câu 9:

Trong mặt phẳng tọa độ Oxy, tìm phương trình đường thẳng

Δ'

là ảnh của đường thẳng

Δ : x + 2 y - 1 = 0

qua phép tịnh tiến theo vectơ

\vec{v} (1; - 1)

A. $Δ' : x + 2 y = 0$

B. $Δ' : x + 2 y - 3 = 0$

C. $Δ' : x + 2 y + 1 = 0$

D. $Δ' : x + 2 y + 2 = 0$

Xem đáp án

Chọn $A (1; 0) \in Δ \Rightarrow T_{\vec{v}} (A) = A' (2; - 1) \in Δ'$

Chọn $B (- 1; 1) \in Δ \Rightarrow T_{\vec{v}} (B) = B' (0; 0) \in Δ'$

Đường thẳng $∆'$ chính là đường thẳng A’B’.

Đường thẳng $∆'$ qua $A' (2; 1)$ và có một vec tơ pháp tuyến $\vec{n} = (1; 2)$ có phương trình là $Δ' : 1 (x - 2) + 2 (y + 1) = 0 \Leftrightarrow x + 2 y = 0$ .

Câu 10:

Trong mặt phẳng tọa độ Oxy, cho $∆ A B C$ biết $A (2; 4), B (5; 1), C (- 1; - 2)$ . Phép tịnh tiến theo vectơ $\vec{B C}$ biến $Δ A B C$ thành $Δ A' B' C'$ tương ứng các điểm. Trọng tâm G’ của $Δ A' B' C'$ là:

A. $G' (- 4; - 2)$

B. $G' (4; 2)$

C. $G' (4; - 2)$

D. $G' (- 4; 4)$

Xem đáp án

Ta có tọa độ trọng tâm $∆ A B C$ là $G (2; 1); \vec{B C} = (- 6; - 3)$ .

T_{\vec{B C}} (G) = G' (x_{G'}; y_{G'}) \Leftrightarrow G \vec{G'} = B \vec{C} \Leftrightarrow \{\begin{cases} x_{G'} = x_{G} + x_{\vec{B C}} \\ y_{G'} = y_{G} + y_{\vec{B C}} \end{cases} \Rightarrow \{\begin{cases} x_{G'} = 2 - 6 = - 4 \\ y_{G'} = 1 - 3 = - 2 \end{cases} \Rightarrow G' (- 4; - 2)

Câu 11:

Trong mặt phẳng Oxy, cho hai đường thẳng song song d và d’ lần lượt có phương trình là $3 x - 2 y = 0$ và $3 x - 2 y + 1 = 0$ . Phép tịnh tiến theo vectơ nào sau đây biến đường thẳng d thành d’?

A. $\vec{v} = (1; - 2)$

B. $\vec{v} = (- 1; - 2)$

C. $\vec{v} = (- 1; - 1)$

D. $\vec{v} = (1; - 1)$

Xem đáp án

Gọi $\vec{v} = (a; b)$ là vectơ tịnh tiến biến d thành d’. Khi đó $M (x; y) \in d$ biến thành điểm $M' (x'; y') \in d'$

Áp dụng công thức $\{\begin{cases} x' = x + a \\ y' = y + b \end{cases} \Rightarrow \{\begin{cases} x = x' - a \\ y = y' - b \end{cases}$

Thay vào phương trình d ta có $3 (x' - a) - 2 (y' - b) = 0 \Leftrightarrow 3 x' - 2 y' - 3 a + 2 b = 0$

Để biến d thành d’ thì $- 3 a + 2 b = 1$

Chọn

a = - 1; b = - 1

hay

\vec{v} = (- 1; - 1)

thỏa mãn

Câu 12:

Trong mặt phẳng tọa độ Oxy, phương trình đường tròn (C') là ảnh của đường tròn qua

(C) : x^{2} + y^{2} - 2 x + 4 y - 1 = 0

với

\vec{v} = (1; 2)

là

A. ${(x + 2)}^{2} + y^{2} = \sqrt{6}$

B. ${(x - 2)}^{2} + y^{2} = 6$

C. $x^{2} + y^{2} - 2 x - 5 = 0$

D. $2 x^{2} + 2 y^{2} - 8 x + 4 = 0$

Xem đáp án

Theo tính chất của phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính.

Ta có đường tròn (C) có tâm $I (1; - 2)$ , bán kính $R = \sqrt{6}$

Với phép tịnh tiến theo $\vec{v} = (1; 2)$ thì ta có $\{\begin{cases} x' = x + 1 \\ y' = y + 2 \end{cases}$

Suy ra $T_{\vec{v}} (I) = I' (2; 0)$

Vậy đường tròn (C') có tâm $I' (2; 0)$ , bán kính $R' = R = \sqrt{6}$ có phương trình ${(x - 2)}^{2} + y^{2} = 6$ .

Câu 13:

Trong mặt phẳng tọa độ Oxy, cho $\vec{v} = (- 2; 1)$ và đường thẳng $d : 2 x - 3 y + 3 = 0; d_{1} : 2 x - 3 y - 5 = 0$ . Biết vectơ $\vec{w} = (a; b)$ có phương vuông góc với đường thẳng d để là ảnh của d qua phép tịnh tiến $T_{\vec{w}}$ . Khi đó a+b bằng:

A. $\frac{6}{13}$

B. $\frac{16}{3}$

C. $\frac{- 8}{13}$

D. $\frac{5}{13}$

Xem đáp án

Đường thẳng d có vec tơ pháp tuyến là $\vec{n} = (2; - 3) \Rightarrow \vec{w} = (2 m; - 3 m)$ .

$T_{\vec{w}} (M) = M' (2 m; 1 - 3 m)$ với $M \in d$ .

$T_{\vec{w}} (d) = d' \Rightarrow d'$ có dạng $2 x - 3 y + β = 0$

Vì d’ qua M’ nên $4 m - 3 + 9 m + β = 0 \Leftrightarrow β = 3 - 13 m$

Vậy $d' : 2 x - 3 y + 3 - 13 m = 0$ . Để $d_{1} \equiv d'$ thì $3 - 13 m = - 5 \Leftrightarrow m = \frac{8}{13}$

Suy ra $\vec{w} = (\frac{16}{23}; - \frac{24}{13}) \Rightarrow a + b = - \frac{8}{13}$

Câu 14:

Cho hình vuông ABCD trong đó $A (- 1; 1), C (3; 5)$ . Phương trình ảnh của đường tròn nội tiếp hình vuông ABCD qua phép tịnh tiến theo vectơ $\vec{v} = \frac{1}{2} \vec{A C}$ là:

A. ${(x - 3)}^{2} + {(y - 5)}^{2} = 4$

B. ${(x + 1)}^{2} + {(y - 1)}^{2} = 16$

C. ${(x - 2)}^{2} + {(y - 1)}^{2} = 8$

D. ${(x - 3)}^{2} + {(y - 5)}^{2} = 16$

Xem đáp án

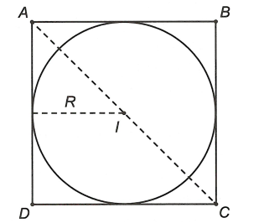
Cho hình vuông ABCD trong đó A(1,-1) , C (3,5) . Phương trình ảnh của đường tròn nội tiếp hình vuông ABCD qua phép tịnh tiến theo vectơ (ảnh 1)

Bán kính của đường tròn (C) là R=2

Ta có $\vec{v} = \frac{1}{2} \vec{A C} = (2; 2)$

Tâm I của đường tròn là trung điểm của đoạn AC nên I(1,3)

Xét $T_{\vec{v}} (I) = I' (x'; y')$ . Ta có $\{\begin{cases} x' = 1 + 2 = 3 \\ y' = 3 + 2 = 5 \end{cases} \Rightarrow I' (3; 5)$

Qua phép tịnh tiến theo vectơ $\vec{v}$ ảnh của (C) là đường tròn (C') có tâm I’ và bán kính R=2.

Vậy ảnh của đường tròn (C) có phương trình là: $(C') : {(x - 3)}^{2} + {(y - 5)}^{2} = 4$ .

Bài tập chuyên đề toán 11 Bài 1: Phép biến hình- phép tịnh tiến có đáp án

Dạng 2: Biểu thức tọa độ của phép tịnh tiến có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương