20 câu hỏi trắc nghiệm thuộc 100 câu trắc nghiệm Đạo hàm nâng cao (P3)

Câu 1:

Cho hàm số $y = \frac{2 x - 1}{x - 1} (C)$ . Số điểm trên đồ thị (C) biết tiếp tuyến với đồ thị hàm số tại M cắt trục 0x; 0y lần lượt tại A; B sao cho $AB = \sqrt{82} OB$

A : không tồn tại

B : 1

C : 2

D : 3

Xem đáp án

Chọn C.

Câu 2:

Tính đạo hàm của hàm số: $y = \sqrt{\frac{1}{2} + \frac{1}{2} \sqrt{\frac{1}{2} + \frac{1}{2} \sqrt{\frac{1}{2} + \frac{1}{2} \cos x}}}$ với x ∈ (0; π).

A. $\frac{1}{8} \sin \frac{x}{8}$

B. $- \frac{1}{8} \sin \frac{x}{8}$

C. $\frac{1}{6} \sin \frac{x}{4}$

D: tất cả sai

Xem đáp án

Chọn B.

Câu 3:

Tính đạo hàm của hàm số: $y = {(\frac{\sin x}{1 + \cos x})}^{3}$

A. $\frac{3 \sin^{2} x}{{(1 + \cos x)}^{3}}$

B. $\frac{3 \cos^{2} x}{{(1 + \cos x)}^{3}}$

C. $- \frac{3 \sin^{2} x}{{(1 + \cos x)}^{3}}$

D. $- \frac{3 \cos^{2} x}{{(1 + \cos x)}^{3}}$

Xem đáp án

Chọn A.

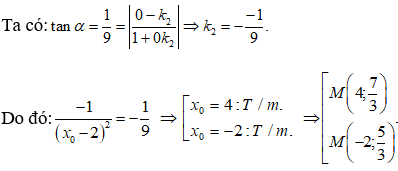
Câu 4:

Tính đạo hàm của hàm số: y = sin³(2x + 1).

A: 6sin²(2x + 1)

B: sin²(2x + 1)cosx

C: sin²(2x + 1)cos(2x + 1)

D: 6sin²(2x + 1)cos(2x + 1)

Xem đáp án

Chọn D.

Bước đầu tiên áp dung công thức với u = sin(2x + 1)

Vậy y’ = (sin³(2x + 1))’ = 3sin²(2x + 1).(sin(2x + 1))’.

Tính (sin(2x + 1))’:

Áp dụng (sin u)’, với u = (2x + 1)

Ta được: (sin(2x + 1))’ = cos(2x + 1).(2x + 1)’ = 2cos(2x + 1).

⇒ y' = 3.sin²(2x + 1).2cos(2x + 1) = 6sin²(2x + 1)cos(2x + 1).

Câu 5:

Tính đạo hàm của hàm số y = 2sin²4x – 3cos³5x.

A: y’ = 8sin8x + 45/2 cos5x.sin10x

B: y’ = 8sin8x - cos5x.sin 10x

C: y’ = 8.sin8x + cos5x

D: y’ = 8sin8x + cos5x.sin6x

Xem đáp án

Chọn A.

Bước đầu tiên áp dụng (u + v)’

y' = (2sin²4x)’ – 3(cos³5x)’

Tính (sin²4x)’:

Áp dụng , với u = sin4x ta được:

(sin²4x)’ = 2sin4x.(sin4x)’ = 2sin4x.cos4x(4x)’ = 4sin8x.

Tương tự: (cos³5x)’ = 3cos²5x.(cos5x)’ = 3cos²5x.(-sin5x).(5x)’

= -15cos²5x.sin5x = -15/2 . cos5x.sin10x.

Kết luận: y’ = 8sin8x + (45/2).cos5x.sin10x.

Câu 6:

Tính đạo hàm của hàm số y = (2 + sin²2x)³.

A: y’ = 6sin2x(2 + sin²2x)

B: y’ = 3sin4x(2 + sin²2x)²

C. y’ = 6sin4x(2 + sin²2x)²

D: Đáp án khác

Xem đáp án

Chọn C.

Áp dụng , với u = 2 + sin²2x.

y' = 3(2 + sin²2x)²(2 + sin²2x)’ = 3(2 + sin²2x)²(sin²2x)’.

Tính (sin²2x)’, áp dụng với u = sin2x

(sin²2x)’ = 2.sin2x(sin2x)’ = 2.sin2x.cos2x(2x)’ = 2sin4x.

⇒ y' = 6sin4x(2 + sin²2x)².

Câu 7:

Tính đạo hàm của hàm số y = sin(cos²x.tan²x).

A. y’ = cos(cos²x.tan²x)(-sin2xtan²x + 2tanx)

B. y’ = cos(cos²x.tan²x) + sin2x.cos²x

C. y’ = cos(cos²x.tan²x)sin2x.(cos²x + 1)

D. y’ = cos(cos²x.tan²x)(sin2x + tan²x).cos²x

Xem đáp án

Chọn A.

Câu 8:

Tính đạo hàm của hàm số $y = \cos^{2} (\frac{\sqrt{x} + 1}{\sqrt{x} - 1})$

A.

B.

C.

D.

Xem đáp án

Chọn B.

Câu 9:

Tính đạo hàm của hàm số $y = \frac{\sin 2 x + \cos 2 x}{2 \sin 2 x - \cos 2 x}$

A.

B.

C.

D.

Xem đáp án

Chọn D.

Câu 10:

Tính đạo hàm của hàm số y = (cos⁴x – sin⁴x)⁵

A: 10cos⁴xsinx

B: 10cos⁴2xsinx

C: 10cos⁴xsin2x

D: -10cos⁴2xsin2x

Xem đáp án

Chọn D.

y = (cos⁴x – sin⁴x)⁵ = [(cos²x – sin²x)(cos²x + sin²x)]⁵ = (cos2x)⁵.

Áp dụng , với u = cos2x

y' = 5.cos⁴2x,(cos2x)’ = 5.cos⁴2x.(-sin2x).(2x)’ = -10cos⁴2x.sin2x.

Câu 11:

Tính đạo hàm của hàm số y = sin²(cos(tan⁴3x))

A: y’ = -sin(2cos(tan⁴3x)).(sin(tan⁴3x)).4tan³3x.(1 + tan³3x).3

B: y’ = -sin(2cos(tan⁴3x)).sin(tan⁴3x)

C: y’ = -sin(2cos(tan⁴3x)).sin(tan⁴3x).sin4x

D: Tất cả sai

Xem đáp án

Chọn A.

Đầu tiên áp dụng với u = sin(cos(tan⁴3x))

y' = 2sin(cos(tan⁴3x)).[sin(cos(tan⁴3x))]’

Sau đó áp dụng (sin u)’, với u = cos(tan⁴3x)

y' = 2sin(cos(tan⁴3x)).cos(cos(tan⁴3x)).(cos(tan⁴3x))’

Áp dụng (cos u)’, với u = tan⁴3x.

y' = -sin(2cos(tan⁴3x)).(sin(tan⁴3x)).(tan⁴3x)’.

Áp dụng với u = tan3x

y’ = -sin(2cos(tan⁴3x)).(sin(tan⁴3x)).4tan³3x.(tan3x)’.

y' = -sin(2cos(tan⁴3x)).(sin(tan⁴3x)).4tan³3x.(1 + tan²3x).(3x)’.

y’ = -sin(2cos(tan⁴3x)).(sin(tan⁴3x)).4tan³3x.(1 + tan³3x).3.

Câu 12:

Tính đạo hàm của hàm số y = sin(cosx) + cos(sinx)

A: sin(2cosx)

B: cos(xsinx)

C: cos(2sinx)

D: -sin(x+cosx)

Xem đáp án

Chọn D.

Bước đầu tiên sử dụng đạo hàm tổng, sau đó sử dụng (sin u)’, (cos u)’.

y' = (sin(cosx))’ + (cos(sinx))’ = cos(cosx).(cosx)’ – sin(sinx).(sinx)’

= -sinx.cos(cosx) – cosx.sin(sinx) = -(sinx.cos(cosx) + cosx.sin(sinx))

= -sin(x + cosx).

Câu 13:

Tính đạo hàm của hàm số $y = \frac{\sin x - x \cos x}{\cos x + x \sin x}$

A.

B.

C.

D.

Xem đáp án

Chọn D.

Câu 14:

Tính đạo hàm của hàm số $y = \tan 2 x + \frac{2}{3} \tan^{3} 2 x + \frac{1}{5} \tan^{5} 2 x$

A: y’ = 2(1 + tan²2x)²

B: y’ = 2(1 + tan²2x)³

C: y’ = -2(1 + tan²2x)²

D: y’ = -2(1 – tan²2x)⁴

Xem đáp án

Chọn B.

Câu 15:

Cho hàm số y = f(x) – cos²x với f(x) là hàm số liên tục trên R . Trong 4 biểu thức dưới đây, biểu thức nào xác định f(x) thỏa mãn y’ = 1, ∀ x ∈ R?

A. $x + \frac{1}{2} \cos 2 x$

B. $x - \frac{1}{2} \cos 2 x$

C. x – sin2x

D. x + sin2x

Xem đáp án

Chọn A.

Ta có: y’ = f’(x) + 2cosxsinx = f’(x) + sin2x

y’(x) = 1 ⇔ f’(x) + sin2x = 1 ⇔ f’(x) = 1 – sin2x ⇒ f(x) = x + ½ cos2x.

Câu 16:

Cho hàm số $f (x) = \{\begin{cases} x^{3} . \sin \frac{1}{x} k h i x \neq 0 \\ 0 k h i x = 0 \end{cases}$ . Đạo hàm f’(x) là biểu thức nào sau đây?

A.

B.

C.

D.

Xem đáp án

Chọn D.

Câu 17:

Cho hàm số f(x) = sin⁶x + cos⁶x + 3sin²xcos²x. Khi đó f’(x) có giá trị bằng bao nhiêu?

A. 1.

B. 2.

C. 0.

D. -1.

Xem đáp án

Chọn C.

f'(x) = 6sin⁵xcosx – 6cos⁵xsinx + 3(2sinxcos³x – 2cosxsin³x)

= 6sinxcosx(sin⁴x – cos⁴x + cos²x – sin²x)

= 6sinxcosx(sin²x – cos²x + cos²x – sin²x) = 0.

Câu 18:

Cho hàm số y = (m + 1)sinx + mcosx – (m + 2)x + 1. Tìm giá trị của m để y’ = 0 có nghiệm?

A.

B. m ≥ 2.

C. -1 ≤ m ≤ 3.

D. m ≤ -2.

Xem đáp án

Chọn A.

y' = (m + 1)cosx – msinx – ( m + 2)

Phương trình y’ = 0 ⇔ (m + 1)cosx – msinx = (m + 2)

Điều kiện phương trình có nghiệm là a² + b² ≥ c²

⇔ (m + 1)² + m² ≥ (m + 2)² ⇔ m² – 2m – 3 ≥ 0

Câu 19:

Cho hàm số y = cos²x + sinx. Phương trình y’ = 0 có bao nhiêu nghiệm thuộc khoảng (0; π)

A. 1 nghiệm.

B. 2 nghiệm.

C. 3 nghiệm.

D. 4 nghiệm.

Xem đáp án

Chọn C.

Câu 20:

Hàm số $y = x \sqrt{x^{2} + 1}$ có đạo hàm cấp 2 bằng :

A.

B.

C.

D.

Xem đáp án

Chọn C.

100 câu trắc nghiệm Đạo hàm nâng cao

100 câu trắc nghiệm Đạo hàm nâng cao (P3)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương