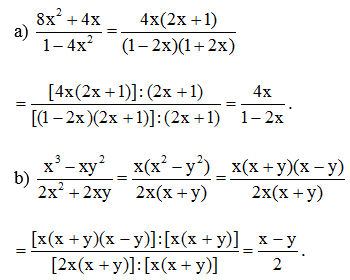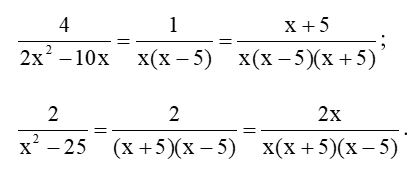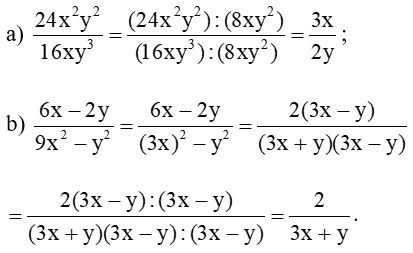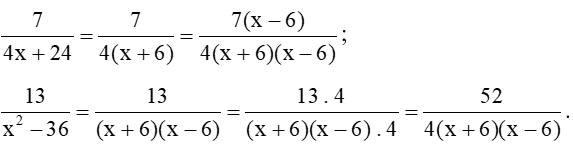Giải SGK Toán 8 (Cánh diều) Bài 1: Phân thức đại số

Giải Toán 8 Bài 1: Phân thức đại số

Khởi động trang 29 Toán 8 Tập 1: Ở lớp 6, ta đã biết kết quả của phép chia số nguyên a cho số nguyên b khác 0 có thể viết dưới dạng $\frac{a}{b}$, ta gọi $\frac{a}{b}$ là phân số. Tương tự, kết quả của phép chia đa thức P cho đa thức Q khác đa thức 0 cũng có thể viết dưới dạng $\frac{P}{Q}$ . Khi đó, biểu thức $\frac{P}{Q}$ được gọi là gì?

Lời giải:

Sau khi học xong bài này ta sẽ giải quyết bài toán này như sau:

Kết quả của phép chia đa thức P cho đa thức Q khác đa thức 0 cũng có thể viết dưới dạng $\frac{P}{Q}$. Khi đó, biểu thức $\frac{P}{Q}$ được gọi là phân thức.

Hoạt động 1 trang 29 Toán 8 Tập 1: Cho biểu thức $\frac{2x+1}{x-2}$.

a) Biểu thức 2x + 1 có phải đa thức hay không?

b) Biểu thức x – 2 có phải đa thức khác đa thức 0 hay không?

Lời giải:

a) Biểu thức 2x + 1 là đa thức.

a) Biểu thức x – 2 là đa thức khác đa thức 0.

Luyện tập 1 trang 30 Toán 8 Tập 1: Trong những biểu thức sau, biểu thức nào là phân thức?

a) $\frac{x^{2}y+x{y}^2}{x-y}$.

b) $\frac{x^2-1}{\frac{1}{x}}$ .

Lời giải:

a) Do x²y + xy² và x – y là các đa thức và đa thức x – y khác đa thức 0 nên biểu thức $\frac{x^{2}y+x{y}^2}{x-y}$ là phân thức.

b) Do biểu thức$\frac{1}{x}$ không phải là các đa thức nên biểu thức $\frac{x^2-1}{\frac{1}{x}}$ không phải là phân thức.

Hoạt động 2 trang 30 Toán 8 Tập 1: Cho hai phân số $\frac{a}{b}$ và $\frac{c}{d}$. Nêu quy tắc để hai phân số bằng nhau.

Lời giải:

Quy tắc để hai phân số bằng nhau là:

Hai phân số $\frac{a}{b}$ và $\frac{c}{d}$ được gọi là bằng nhau nếu a . d = b . c, viết là $\frac{a}{b}$ = $\frac{c}{d}$.

Luyện tập 2 trang 30 Toán 8 Tập 1: Mỗi cặp phân thức sau có bằng nhau không? Vì sao?

a) $\frac{x+y}{x^2-y^2}$ và $\frac{1}{x-y}$.

b) $\frac{x}{x^2-1}$ và .$\frac{1}{x-1}$

Lời giải:

a) Ta có: (x + y)(x – y) = x² – y² và (x² – y²) . 1 = x² – y².

Nên (x + y)(x – y) = (x² – y²) . 1.

Vậy $\frac{x+y}{x^2-y^2}$ = $\frac{1}{x-y}$.

b) Ta có: x(x – 1) = x² – x và (x² – 1) . 1 = x² – 1

Do x(x – 1) ≠ (x² – 1) . 1 nên hai phân thức$\frac{x}{x^2-1}$ và$\frac{1}{x-1}$ không bằng nhau.

Luyện tập 3 trang 32 Toán 8 Tập 1: Dùng tính chất cơ bản của phân thức, hãy giải thích vì sao có thể viết: $\frac{3x+y}{y}=\frac{3xy+y^2}{y^2}$.

Lời giải:

Nhân cả tử và mẫu của phân thức đã cho với y, ta được:

$\frac{3xy+y}{y}=\frac{(3x+y).y}{y.y}=\frac{3xy+y^2}{y^2}$ (theo tính chất cơ bản của phân thức).

Hoạt động 4 trang 32 Toán 8 Tập 1: Cho phân thức $\frac{4x^{2}y}{6x{y}^2}$ .

a) Tìm nhân tử chung của tử và mẫu.

b) Tìm phân thức nhận được sau khi chia cả tử và mẫu cho nhân tử chung đó.

Lời giải:

a) Nhân tử chung của tử và mẫu là 2xy.

b) Ta có : $\frac{4x^{2}y}{6x{y}^2}=\frac{4x^{2y}:2xy}{6x{y}^2:2xy}=\frac{2x}{3y}$ .

Vậy sau khi chia cả tử và mẫu cho nhân tử chung thì phân thức nhận được là$\frac{2x}{3y}$ .

Luyện tập 4 trang 32 Toán 8 Tập 1: Rút gọn mỗi phân thức sau:

a) $\frac{8x^2+4x}{1-4x^2}$ ;

b) $\frac{x^3-x{y}^2}{2x^2+2xy}$ .

Lời giải:

Hoạt động 5 trang 33 Toán 8 Tập 1: Cho hai phân thức $\frac{1}{x^{2}y}$ và $\frac{1}{x{y}^2}$.

a) Hãy nhân cả tử và mẫu của phân thức thứ nhất với y và nhân cả tử và mẫu của phân thức thứ hai với x.

b) Nhận xét gì về mẫu của hai phân thức thu được.

Lời giải:

Cho hai phân thức $\frac{1}{x^{2}y}$ và $\frac{1}{x{y}^2}$.

a) • Nhân cả tử và mẫu của phân thức thứ nhất với y, ta được:

$\frac{1}{x^{2}y}=\frac{1.y}{x^{2}y.y}=\frac{y}{x^2{y}^2}$.

• Nhân cả tử và mẫu của phân thức thứ hai với x, ta được:

$\frac{1}{x{y}^2}=\frac{1.x}{x{y}^2.x}=\frac{x}{x^2{y}^2}$.

b) Mẫu của hai phân thức thu được bằng nhau và đều bằng x²y².

Hoạt động 6 trang 33 Toán 8 Tập 1: Tìm MTC của hai phân thức $\frac{5}{2x+6}$ và $\frac{3}{x^2-9}$.

Lời giải:

Để tìm MTC của hai phân thức trên, ta có thể làm như sau:

Bước 1. Phân tích mẫu của mỗi phân thức đã cho thành nhân tử

2x + 6 = 2(x + 3); x² – 9 = (x – 3)(x + 3).

Bước 2. Chọn MTC là: 2(x – 3)(x + 3).

Cách tìm mẫu thức như bảng sau:

Hoạt động 7 trang 33 Toán 8 Tập 1: Quy đồng mẫu thức hai phân thức $\frac{1}{x^2+x}$ và $\frac{1}{x^2-x}$.

Lời giải:

Để quy đồng mẫu thức của hai phân thức trên, ta có thể làm như sau:

Bước 1. Tìm mẫu thức chung

Chọn MTC là: x(x – 1)(x + 1).

Bước 2. Tìm nhân tử phụ của mỗi mẫu thức (bằng cách chia MTC cho từng mẫu)

[x(x – 1)(x + 1)] : x(x + 1) = x – 1; [x(x – 1)(x + 1)] : x(x – 1) = x + 1.

Bước 3. Nhân cả tử và mẫu của mỗi phân thức đã cho với nhân tử phụ tương ứng

$\frac{2}{x^2+x}=\frac{1}{x(x+1)}=\frac{x-1}{x(x+1)(x-1)}$;

$\frac{1}{x^2-x}=\frac{1}{x(x-1)}=\frac{x+1}{x(x+1)(x-1)}$.

Luyện tập 5 trang 34 Toán 8 Tập 1: Quy đồng mẫu thức các phân thức trong mỗi trường hợp sau:

a) $\frac{5}{2x^2{y}^3}$ và $\frac{3}{x{y}^4}$;

b) $\frac{4}{2x^2-10x}$ và $\frac{2}{x^2-25}$.

Lời giải:

a) $\frac{5}{2x^2{y}^3}$ và $\frac{3}{x{y}^4}$

Ta có MTC: 2x²y⁴.

Quy đồng mẫu thức các phân thức, ta được:

$\frac{5}{2x^2{y}^3}=\frac{5.y}{2x^2{y}^3.y}=\frac{5y}{2x^2{y}^4}$; $\frac{3}{x{y}^4}=\frac{3.2x}{x{y}^4.2x}=\frac{6x}{2x^2{y}^4}$.

b) $\frac{4}{2x^2-10x}$ và $\frac{2}{x^2-25}$.

Ta có $\frac{4}{2x^2-10x}=\frac{2}{2x(x-5)}=\frac{1}{x(x-5)}$.

x² – 25 = x² – 5² = (x + 5)(x – 5).

Suy ra MTC: x(x + 5)(x – 5).

Quy đồng mẫu thức các phân thức, ta được:

Hoạt động 8 trang 34 Toán 8 Tập 1: Cho phân thức $\frac{2x^2-x+1}{x-2}$. Tìm giá trị của x sao cho mẫu x – 2 ≠ 0.

Lời giải:

Để mẫu x – 2 ≠ 0 thì x≠ 2.

Vậy giá trị của x sao cho mẫu x – 2 ≠ 0 là x≠ 2.

Bài 1 trang 37 Toán 8 Tập 1: Viết điều kiện xác định của mỗi phân thức sau:

a) $\frac{y}{3y+3}$;

b) $\frac{4x}{x^2+16}$;

c) $\frac{x+y}{x-y}$.

Lời giải:

a) Điều kiện xác định của phân thức $\frac{y}{3y+3}$ là3y + 3 ≠ 0;

b) Điều kiện xác định của phân thức $\frac{4x}{x^2+16}$ là x² + 16 ≠ 0;

c) Điều kiện xác định của phân thức $\frac{x+y}{x-y}$ là x – y ≠ 0.

Bài 2 trang 37 Toán 8 Tập 1: Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:

a) $\frac{3x}{2}=\frac{15xy}{10y}$;

b) $\frac{3x-3y}{2y-2x}=\frac{-3}{2}$;

c) $\frac{x^2-x+1}{x}=\frac{x^3+1}{x(x+1)}$.

Lời giải:

a) Ta có: 3x . 10y = 30xy và 2 . 15xy = 30xy

Nên 3x . 10y = 2 . 15xy.

Do đó $\frac{3x}{2}=\frac{15xy}{10y}$.

b) Ta có (3x – 3y) . 2 = 6x – 6y và –3(2y – 2x) = – 6y + 6x = 6x – 6y.

Nên (3x – 3y) . 2 = –3(2y – 2x).

Do đó $\frac{3x-3y}{2y-2x}=\frac{-3}{2}$.

c) Ta có (x² – x + 1) . x(x + 1) = x(x + 1)(x² – x + 1) = x(x³ + 1);

Vì (x² – x + 1) . x(x + 1) = x(x³ + 1) nên $\frac{x^2-x+1}{x}=\frac{x^3+1}{x(x+1)}$.

Bài 3 trang 37 Toán 8 Tập 1: Rút gọn mỗi phân thức sau:

a) $\frac{24x^2{y}^2}{16x{y}^3}$;

b) $\frac{6x-2y}{9x^2-y^2}$.

Lời giải:

Bài 4 trang 37 Toán 8 Tập 1: Quy đồng mẫu thức các phân thức trong mỗi trường hợp sau:

a) $\frac{2}{x-3y}$ và $\frac{3}{x+3y}$ ;

b) $\frac{7}{4x+24}$ và $\frac{13}{x^2-36}$ .

Lời giải:

a) Ta có MTC: (x – 3y)(x + 3y)

Quy đồng mẫu thức các phân thức, ta được:

.

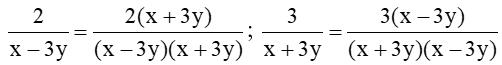
b) Ta có: 4x + 24 = 4(x + 6); x² – 36 = (x + 6)(x – 6).

Suy ra MTC: 4(x + 6)(x – 6).

Quy đồng mẫu thức các phân thức, ta được:

Bài 5 trang 37 Toán 8 Tập 1: Cho hình chữ nhật ABCD và MNPQ như Hình 1 (các số đo trên hình tính theo đơn vị centimét).

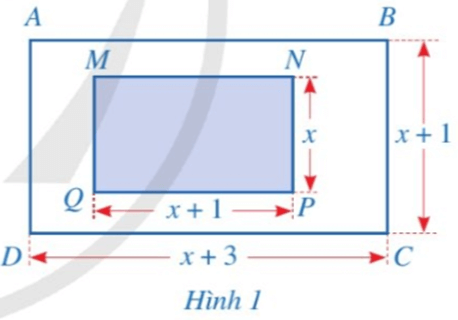
a) Viết phân thức biểu thị tỉ số diện tích của hình chữ nhật ABCD và hình chữ nhật MNPQ.

b) Tính giá trị của phân thức đó tại x = 2 và tại x = 5.

Lời giải:

a) Trong Hình 1:

• Hình chữ nhật ABCD có chiều dài là x + 3 (cm); chiều rộng là x + 1 (cm).

Biểu thức biểu thị diện tích của hình chữ nhật ABCD là: (x + 3)(x + 1) (cm²).

• Hình chữ nhật MNPQ có chiều dài là x + 1 (cm); chiều rộng là x (cm).

Biểu thức biểu thị diện tích của hình chữ nhật ABCD là: x(x + 1) (cm²).

Phân thức biểu thị tỉ số diện tích của hình chữ nhật ABCD và hình chữ nhật MNPQ là: $\frac{(x+3)(x+1)}{x(x+1)}=\frac{x+3}{x}$.

b) Điều kiện xác định của phân thức $\frac{x+3}{x}$ là x≠ 0.

• Ta thấy x = 2≠ 0.

Do đó, giá trị của phân thức $\frac{x+3}{x}$ tại x = 2 là: $\frac{2+3}{2}=\frac{5}{2}$ .

• Ta thấy x = 5≠ 0.

Do đó, giá trị của phân thức $\frac{x+3}{x}$ tại x = 5 là: $\frac{5+3}{5}=\frac{8}{5}$ .

Bài 6 trang 37 Toán 8 Tập 1: Chị Hà mở một xưởng thủ công với vốn đầu tư ban đầu (xây dựng nhà xưởng, mua máy móc, ...) là 80 triệu. Biết chi phí để sản xuất (tiền mua vật liệu, lương công nhân) của 1 sản phẩm là 15 nghìn đồng. Gọi x là số sản phẩm mà xưởng của chị Hà làm được.

a) Viết phân thức biểu thị số tiền thực (đơn vị nghìn đồng) đã bỏ ra để làm được x sản phẩm.

b) Viết phân thức biểu thị chi phí thực (đơn vị nghìn đồng) để tạo ra 1 sản phẩm theo x.

c) Tính chi phí thực để tạo ra 1 sản phẩm nếu x = 100; x = 1 000. Nhận xét về chi phí thực để tạo ra 1 sản phẩm nếu x ngày càng tăng.

Lời giải:

a) Đổi: 80 triệu = 80 000 nghìn đồng.

Chi phí để sản xuất của 1 sản phẩm là 15 nghìn đồng.

Khi đó, chi phí để sản xuất của x sản phẩm là 15x nghìn đồng.

Do đó, số tiền thực (đơn vị nghìn đồng) đã bỏ ra để làm được x sản phẩm là:

80 000 + 15x (nghìn đồng).

Vậy phân thức biểu thị số tiền thực đã bỏ ra để làm được x sản phẩm là $\frac{80000+15x}{1}$ (nghìn đồng).

b) Phân thức biểu thị chi phí thực để tạo ra 1 sản phẩm theo x là: $\frac{80000+15x}{x}$ (nghìn đồng).

c) • Chi phí thực để tạo ra 1 sản phẩm nếu x = 100 là:

$\frac{80000+15.100}{100}=\frac{80000+1500}{100}=\frac{81500}{100}=815$ (nghìn đồng).

• Chi phí thực để tạo ra 1 sản phẩm nếu x = 1 000 là:

$\frac{80000+15.1000}{1000}=\frac{80000+15000}{100}=\frac{9500}{100}=95$ (nghìn đồng).

Nhận xét: Nếu x ngày càng tăng thì chi phí thực để tạo ra 1 sản phẩm càng giảm.

Từ đó ta kết luận thời gian sử dụng càng lâu thì càng tiết kiệm chi phí.

Xem thêm lời giải bài tập SGK Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài 4: Luyện tập hằng đẳng thức vào phân tích đa thức thành nhân tử

Bài tập cuối chương 1

Bài 2: Phép cộng, phép trừ phân thức đại số

Bài 3: Phép nhân, phép chia phân thức đại số

Bài tập cuối chương 2