Giải SGK Toán 11 (Cánh diều) Bài 3: Đạo hàm cấp hai

Giải Toán 11 Bài 3: Đạo hàm cấp hai

Câu hỏi khởi động trang 73 Toán 11 Tập 2: Khi tham gia giao thông, một ô tô đang chạy với vận tốc 54 km/h (Hình 6) thì tài xế thấy một vật cản phía trước. Để tránh va chạm vật cản, người tài xế đã hãm phanh, ô tô giảm vận tốc cho đến khi dừng hẳn.

Đại lượng đặc trưng cho sự giảm vận tốc thể hiện kiến thức gì trong toán học?

Lời giải:

Để trả lời được câu hỏi trên, chúng ta cùng tìm hiểu bài học này.

I. Định nghĩa

Hoạt động 1 trang 73 Toán 11 Tập 2:Xét hàm số y = x³ – 4x² + 5.

a) Tìm y'.

b) Tìm đạo hàm của hàm số y'

Lời giải:

a) Từ y = x³ – 4x² + 5 ta có y' = 3x² – 8x.

b) Đạo hàm của hàm số y' là (3x² – 8x)' = 6x – 8

Luyện tập trang 73 Toán 11 Tập 2: Tìm đạo hàm cấp hai của hàm số y = sin3x

Lời giải:

Từ y = sin3x ta có y' = (sin3x)' = 3cos3x.

Do đó y'' = (3cos3x)' = 3.3.(– sin3x) = –9sin3x

II. Ý nghĩa cơ học của đạo hàm cấp 2

Hoạt động 2 trang 74 Toán 11 Tập 2: Một vật rơi tự do theo phương thẳng đứng có phương trình chuyển động $s=\frac{1}{2}g{t}^2,$trong đó g là gia tốc rơi tự do, g ≈ 9,8 m/s².

a) Tính vận tốc tức thời v(t) tại thời điểm t₀ = 4 (s); t₁ = 4,1 (s).

b) Tính tỉ số $\frac{\Delta v}{\Delta t}$ trong khoảng thời gian ∆t = t₁ – t₀.

Lời giải:

a) Vận tốc tức thời: $v\left(t\right)=s\text{'}\left(t\right)={\left(\frac{1}{2}g{t}^2\right)}^{\text{'}}=gt$  (m/s).

Tại thời điểm t₀ = 4 (s) thì v(4) ≈ 9,8 . 4 = 39,2 (m/s);

Tại thời điểm t₁ = 4,1 (s) thì v(4,1) ≈ 9,8 . 4,1 = 40,18 (m/s).

b) Ta có  $\frac{\Delta v}{\Delta t}=\frac{v\left(4,1\right)-v\left(4\right)}{t_1-t_0}=\frac{40,18-39,2}{4,1-4}=9,8.$

Bài 1 trang 75 Toán 11 Tập 2: Tìm đạo hàm cấp hai của mỗi hàm số sau:

a)$y=\frac{1}{2x+3};$

b) y = log₃x;              

c) y = 2^x.

Lời giải:

a) Xét hàm số $y=\frac{1}{2x+3}$ xác định với mọi $x\ne -\frac{3}{2}$

Với $x\ne -\frac{3}{2}$ta có: 

$y^{\text{'}}=-\frac{{\left(2x+3\right)}^{\text{'}}}{{\left(2x+3\right)}^2}=-\frac{2}{{\left(2x+3\right)}^2}$

Suy ra $y^{\text{'}\text{'}}={\left[-\frac{2}{{\left(2x+3\right)}^2}\right]}^{\text{'}}=2\cdot \frac{{\left[{\left(2x+3\right)}^2\right]}^{\text{'}}}{{\left(2x+3\right)}^4}$

               $=2\cdot \frac{2\cdot {\left(2x+3\right)}^{\text{'}}\cdot \left(2x+3\right)}{{\left(2x+3\right)}^4}$

              $=2\cdot \frac{2\cdot 2\cdot \left(2x+3\right)}{{\left(2x+3\right)}^4}=\frac{8}{{\left(2x+3\right)}^3}.$

b) Xét hàm số y = log₃x xác định với mọi x > 0.

Với x > 0, ta có: $y^{\text{'}}={\left(lo{g}_{3}x\right)}^{\text{'}}=\frac{1}{x\ln 3}$

Suy ra $y^{\text{'}\text{'}}={\left(\frac{1}{x\ln 3}\right)}^{\text{'}}=-\frac{{\left(x\ln 3\right)}^{\text{'}}}{{\left(x\ln 3\right)}^2}=-\frac{\ln 3}{x^2{\ln }^{2}3}=\frac{-1}{x^2\ln 3}.$

c) Xét hàm số y = 2^x, ta có: y' = (2^x)' = 2^x.ln2

Suy ra y'' = (2^x.ln2)' = ln2.2^x.ln2 = 2^x.ln²2.

Bài 2 trang 75 Toán 11 Tập 2: Tính đạo hàm cấp hai của mỗi hàm số sau:

a) y = 3x² – 4x + 5 tại điểm x₀ = –2;

b) y = log₃(2x + 1) tại điểm x₀ = 3;

c) y = e^{4x + 3} tại điểm x₀ = 1;

d) $y=\sin \left(2x+\frac{\pi }{3}\right)$ tại điểm $x_0=\frac{\pi }{6};$

e) $y=\cos \left(3x-\frac{\pi }{6}\right)$ tại điểm x₀ = 0.

Lời giải:

a) Xét hàm số y = 3x² – 4x + 5, ta có:

y' = 6x – 4;

y'' = 6.

Do đó: y''(–2) = 6.

b) Xét hàm số y = log₃(2x + 1), ta có:

$y^{\text{'}}={\left[lo{g}_3\left(2x+1\right)\right]}^{\text{'}}=\frac{{\left(2x+1\right)}^{\text{'}}}{\left(2x+1\right)\ln 3}=\frac{2}{\left(2x+1\right)\ln 3};$

$y^{\text{'}\text{'}}={\left[\frac{2}{\left(2x+1\right)\ln 3}\right]}^{\text{'}}=\frac{-2\cdot {\left[\left(2x+1\right)\ln 3\right]}^{\text{'}}}{{\left[\left(2x+3\right)\ln 3\right]}^2}$$=\frac{-2\ln 3\cdot 2}{{\left(2x+3\right)}^2{\ln }^{2}3}=\frac{-4}{{\left(2x+3\right)}^2\ln 3}.$

Do đó:  $y^{\text{'}\text{'}}\left(3\right)=\frac{-4}{{\left(2\cdot 3+3\right)}^2\ln 3}=\frac{-4}{7^2\cdot \ln 3}=\frac{-4}{49\ln 3}$

c) Xét hàm số y = e^{4x + 3}, ta có:

y' = (e^{4x + 3})' = (4x + 3)'. e^{4x + 3} =  4e^{4x + 3};

y'' = (4e^{4x + 3})' = 4.(4x + 3)'.e^{4x + 3} = 16e^{4x + 3}.

Do đó: y''(1) = 16e^{4.1 + 3} = 16e⁷.

d) Xét hàm số $y=\sin \left(2x+\frac{\pi }{3}\right),$ta có:

$y^{\text{'}}={\left[\sin \left(2x+\frac{\pi }{3}\right)\right]}^{\text{'}}={\left(2x+\frac{\pi }{3}\right)}^{\text{'}}\cdot \cos \left(2x+\frac{\pi }{3}\right)=2\cos \left(2x+\frac{\pi }{3}\right);$

$y^{\text{'}\text{'}}={\left[2\cos \left(2x+\frac{\pi }{3}\right)\right]}^{\text{'}}=2\cdot {\left(2x+\frac{\pi }{3}\right)}^{\text{'}}\cdot \left[-\sin \left(2x+\frac{\pi }{3}\right)\right]=-4\sin \left(2x+\frac{\pi }{3}\right).$

 $y^{\text{'}\text{'}}\left(\frac{\pi }{6}\right)=-4\sin \left(2\cdot \frac{\pi }{6}+\frac{\pi }{3}\right)=-4\sin \frac{2\pi }{3}=-4\cdot \frac{\sqrt{3}}{2}=-2\sqrt{3}.$

e) Xét hàm số $y=\cos \left(3x-\frac{\pi }{6}\right),$ ta có:

 $y^{\text{'}}=\left[\cos \left(3x-\frac{\pi }{6}\right)\right]={\left(3x-\frac{\pi }{6}\right)}^{\text{'}}\cdot \left[-\sin \left(3x-\frac{\pi }{6}\right)\right]=-3\sin \left(3x-\frac{\pi }{6}\right);$

$y^{\text{'}\text{'}}={\left[-3\sin \left(3x-\frac{\pi }{6}\right)\right]}^{\text{'}}=-3{\left(3x-\frac{\pi }{6}\right)}^{\text{'}}\cdot \cos \left(3x-\frac{\pi }{6}\right)=-9\cos \left(3x-\frac{\pi }{6}\right).$

Do đó:  $y^{\text{'}\text{'}}\left(0\right)=-9\cos \left(0-\frac{\pi }{6}\right)=-9\cos \left(-\frac{\pi }{6}\right)=-9\cdot \frac{\sqrt{3}}{2}=\frac{-9\sqrt{3}}{2}.$

Bài 3 trang 75 Toán 11 Tập 2: Một vật rơi tự do theo phương thẳng đứng có phương trình chuyển động trong đó g là gia tốc rơi tự do, g ≈ 9,8 m/s².

a) Tính vận tốc tức thời của vật tại thời điểm t₀ = 2 (s).

b) Tính gia tốc tức thời của vật tại thời điểm t₀ = 2 (s).

Lời giải:

Xét hàm số $s\left(t\right)=\frac{1}{2}g{t}^2.$

a) Vận tốc tức thời của vật: v(t) = s'(t) = gt.

Tại thời điểm t₀ = 2 (s) có: v(2) ≈ 9,8 . 2 = 19,6 (m/s).

b) Gia tốc tức thời của vật: a(t) = v'(t) = g.

Tại thời điểm t₀ = 2 (s) có: a(2) ≈ 9,8 (m/s²).

Bài 4 trang 75 Toán 11 Tập 2: Một chất điểm chuyển động theo phương trình s(t) = t³ – 3t² + 8t + 1, trong đó t > 0, t tính bằng giây và s(t) tính bằng mét. Tính vận tốc tức thời, gia tốc tức thời của chất điểm:

a) Tại thời điểm t = 3 (s);

b) Tại thời điểm mà s(t) = 7 (m)

Lời giải:

Xét hàm số s(t) = t³ – 3t² + 8t + 1.

Suy ra v(t) = s'(t) = 3t² – 6t + 8;

          a(t) = v'(t) = 6t – 6.

a) Vận tốc tức thời tại thời điểm t = 3 (s) là v(3) = 3.3² – 6.3 + 8 = 17 (m/s).

Gia tốc tức thời tại thời điểm t = 3 (s) là a(3) = 6.3 – 6 = 12 (m/s²).

b) Tại thời điểm s(t) = 7 thì t³ – 3t² + 8t + 1 = 7

Do đó t³ – 3t² + 8t – 6 = 0.

Suy ra t = 1 (s)

Vận tốc tức thời tại thời điểm t = 1 (s) là v(1) = 3.1² – 6.1 + 8 = 5 (m/s).

Gia tốc tức thời tại thời điểm t = 1 (s) là a(1) = 6.1 – 6 = 0 (m/s²).

Bài 5 trang 75 Toán 11 Tập 2: Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát như Hình 7, có phương trình chuyển động x(t) = 4sint, trong đó t tính bằng giây và x(t)  tính bằng centimet.

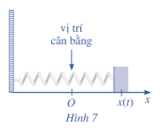
a) Tìm phương trình theo thời gian của vận tốc tức thời và gia tốc tức thời của con lắc.

b) Tính vận tốc tức thời và gia tốc tức thời của con lắc tại thời điểm $t=\frac{2\pi }{3}$(s). Tại thời điểm đó, con lắc đi theo chiều dương hay chiều âm của trục Ox?

Lời giải:

a) Phương trình vận tốc tức thời của con lắc là:

v(t) = x'(t) = (4sint)' = 4cost.

Phương trình gia tốc tức thời của con lắc là:

a(t) = v'(t) = (4cost)' = 4(–sint) = –4sint.

b) Vận tốc tức thời của con lắc tại  $t=\frac{2\pi }{3}$(s) là:

$v\left(\frac{2\pi }{3}\right)=4cos\frac{2\pi }{3}=4\cdot \left(-\frac{1}{2}\right)=-2 (m/s).$

Gia tốc tức thời của con lắc tại $t=\frac{2\pi }{3}$(s)là:

$a\left(\frac{2\pi }{3}\right)=–4sin\frac{2\pi }{3}=-4\cdot \frac{\sqrt{3}}{2}=-2\sqrt{3}$(m/s²).

Do vận tốc tức thời tại thời điểm $t=\frac{2\pi }{3}$(s) mang giá trị âm nên con lắc lúc này đang di chuyển theo chiều âm của trục Ox.

Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác: