Giải Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng
Đường thẳng vuông góc với mặt phẳng được hiểu như thế nào?
Lời giải:
Đường thẳng vuông góc với mặt phẳng được hiểu là đường thẳng nằm thẳng đứng so với mặt phẳng.
1. Định nghĩa
Lời giải:
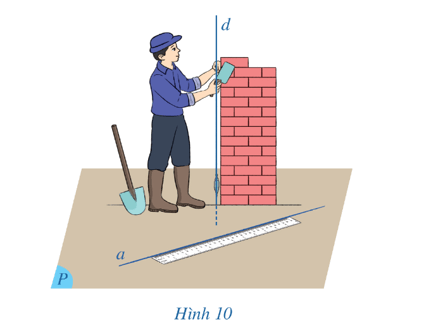
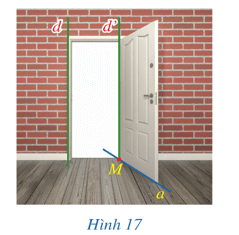
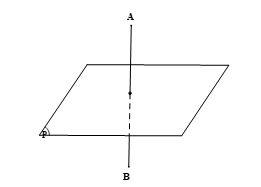
Quan sát Hình 10 ta dự đoán rằng đường thẳng d và đường thẳng a vuông góc với nhau.
2. Điều kiện để đường thẳng vuông góc với mặt phẳng
Lời giải:
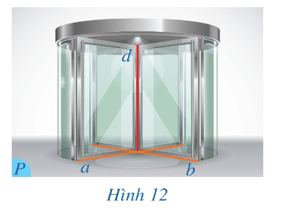
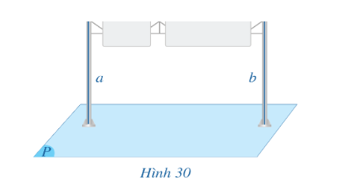
Ta thấy: khi a và b thay đổi (đóng mở cửa) thì đường thẳng d luôn vuông góc với cả hai đường thẳng a và b.
Như vậy ta có thể nói rằng đường thẳng d vuông góc với mọi đường thẳng a và b trong mặt phẳng (P) hay đường thẳng d vuông góc với mặt phẳng (P).
Lời giải:
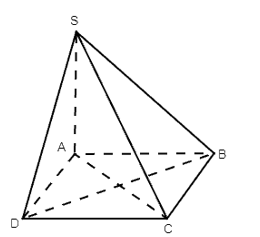
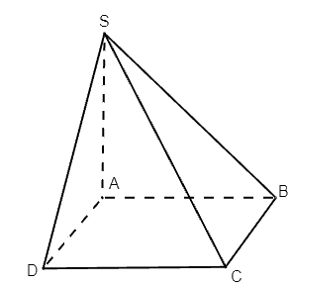
Do SA ⊥ (ABCD), BD ⊂ (ABCD).
Suy ra SA ⊥ BD hay BD ⊥ SA.
Vì ABCD là hình thoi nên BD ⊥ AC.
Ta có: BD ⊥ SA, BD ⊥ AC; SA ∩ AC = A trong (SAC)
Suy ra BD ⊥ (SAC).
3. Tính chất
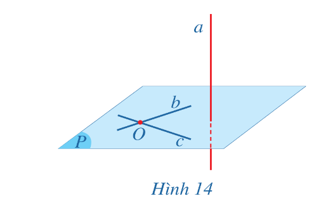
a) Mặt phẳng (P) đi qua hai đường thẳng b, c có vuông góc với đường thẳng a hay không?
b) Có bao nhiêu mặt phẳng đi qua điểm O và vuông góc với đường thẳng a?
Lời giải:
a) Ta có: a ⊥ b, a ⊥ c và b ∩ c = O trong (P).
Suy ra a ⊥ (P).
Vậy mặt phẳng (P) đi qua hai đường thẳng b, c có vuông góc với đường thẳng a.
b) Theo câu a, đường thẳng a vuông góc với mặt phẳng (P), với mặt phẳng (P) đi qua hai đường thẳng b, c cùng vuông góc với đường thẳng a và b ∩ c = O.
Mà qua hai đường thẳng b và c cắt nhau, có một và chỉ một mặt phẳng, tức là tồn tại duy nhất một mặt phẳng đi qua hai đường thẳng cắt nhau b và c.
Vậy chỉ có duy nhất 1 mặt phẳng đi qua điểm O và vuông góc với a.
Lời giải:
Giả sử (P) là mặt phẳng đi qua M và vuông góc với đường thẳng d.
Khi đó ta có đường thẳng d’ đi qua M và d // d’ nên d’ ⊥ (P) tại M.
Lại có a đi qua M và a ⊥ d’ nên a ⊂ (P).
Vậy đường thẳng a luôn nằm trên mặt phẳng đi qua điểm M cố định và vuông góc với đường thẳng d.
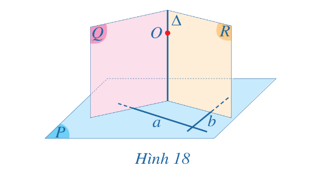
a) Giao tuyến ∆ của hai mặt phẳng (Q), (R) có vuông góc với mặt phẳng (P) hay không?
b) Có bao nhiêu đường thẳng đi qua O và vuông góc với (P)?
Lời giải:
a) Do a ⊥ (Q) và ∆ ⊂ (Q) nên a ⊥ ∆.
b ⊥ (R) và ∆ ⊂ (R) nên b ⊥ ∆.
Mà a, b là hai đường thẳng cắt nhau thuộc mặt phẳng (P)
Suy ra ∆ ⊥ (P).
Vậy giao tuyến ∆ của hai mặt phẳng (Q), (R) có vuông góc với mặt phẳng (P).
b) Theo câu a, ta có ∆ ⊥ (P) với ∆ là giao tuyến của hai mặt phẳng (Q), (R); với hai mặt phẳng (Q), (R) lần lượt đi qua O và vuông góc a, b.
Vì hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng. Tức là tồn tại duy nhất một đường thẳng ∆ đi qua O (điểm chung của 2 mặt phẳng (Q) và (R)).
Vậy có duy nhất một đường thẳng đi qua O và vuông góc với (P).
Lời giải:
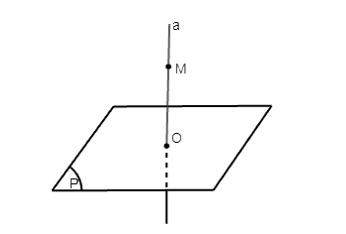
Ta có a ⊥ (P) tại O.
Mặt khác, có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước, tức là tồn tại duy nhất đường thẳng a đi qua điểm O và vuông góc với mặt phẳng (P).
Nên nếu OM ⊥ (P) thì M ∈ a.
4. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng
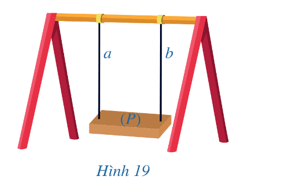
Quan sát Hình 19 và cho biết:
a) Nếu hai đường thẳng a và b song song với nhau và mặt phẳng (P) vuông góc với đường thẳng a thì mặt phẳng (P) có vuông góc với đường thẳng b hay không;
b) Nếu hai đường thẳng a và b cùng vuông góc với mặt phẳng (P) thì chúng có song song với nhau hay không.
Lời giải:
Quan sát Hình 19 ta thấy:
a) Nếu hai đường thẳng a và b song song với nhau và mặt phẳng (P) vuông góc với đường thẳng a thì mặt phẳng (P) có vuông góc với đường thẳng b.
b) Nếu hai đường thẳng a và b cùng vuông góc với mặt phẳng (P) thì chúng có song song với nhau.
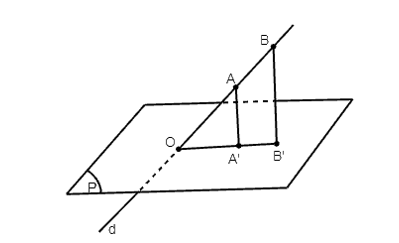
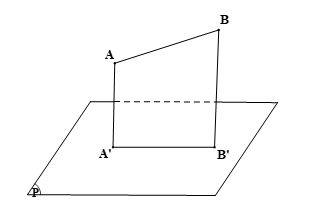
AA'
Lời giải:
Do AA’ ⊥ (P), BB’ ⊥ (P) nên suy ra AA’ // BB’.
Hơn nữa O, A, B thẳng hàng nên suy ra O, A’, B’ cũng thẳng hàng (tính chất phép chiếu song song).
Xét tam giác OBB’ có AA’ // BB’ nên theo hệ quả định lí Thalès ta có:
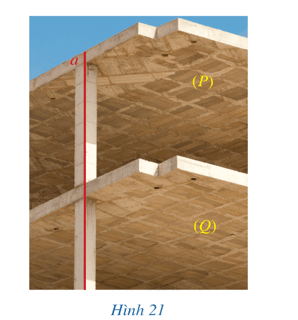
Quan sát Hình 21 và cho biết:
a) Nếu hai mặt phẳng (P), (Q) song song với nhau và đường thẳng a vuông góc với mặt phẳng (P) thì đường thẳng a có vuông góc với mặt phẳng (Q) hay không;
b) Nếu hai mặt phẳng (P), (Q) cùng vuông góc với đường thẳng a thì chúng có song song với nhau hay không.
Lời giải:
Quan sát Hình 21 ta thấy:
a) Nếu hai mặt phẳng (P), (Q) song song với nhau và đường thẳng a vuông góc với mặt phẳng (P) thì đường thẳng a có vuông góc với mặt phẳng (Q).
b) Nếu hai mặt phẳng (P), (Q) cùng vuông góc với đường thẳng a thì chúng có song song với nhau.
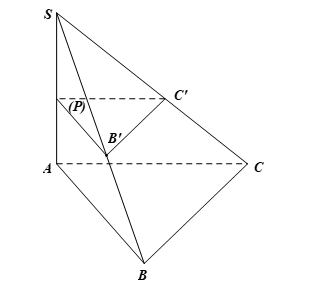
Lời giải:
Ta có: (ABC) ⊥ SA, (P) ⊥ SA nên suy ra (P) // (ABC).
Dễ thấy: (SBC) ∩ (P) = B’C’ và (SBC) ∩ (ABC) = BC.
Từ các kết quả trên ta có: B’C’ // BC.
5. Phép chiếu vuông góc
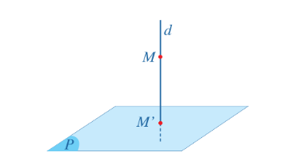
Hoạt động 7 trang 85 Toán 11 Tập 2: Cho mặt phẳng (P). Xét một điểm M tuỳ ý trong không gian.
a) Có bao nhiêu đường thẳng d đi qua điểm M và vuông góc với mặt phẳng (P)?
b) Đường thẳng d cắt mặt phẳng (P) tại bao nhiêu giao điểm?
Lời giải:
a) Vì có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước. Nên có một đường thẳng d đi qua điểm M và vuông góc với mặt phẳng (P).
b) Do đường thẳng d vuông góc với mặt phẳng (P) nên đường thẳng d cắt mặt phẳng (P) tại một giao điểm.
Lời giải:
⦁ Nếu đoạn thẳng AB vuông góc với mặt phẳng (P) thì hình chiếu của đoạn thẳng AB trên (P) là một điểm, điểm đó là giao điểm của đường thẳng AB và (P).
⦁ Nếu đoạn thẳng AB không vuông góc với mặt phẳng (P) thì ta cần thực hiện các bước sau đây để xác định hình chiếu của đoạn thẳng AB trên mặt phẳng (P):
Bước 1. Tìm hình chiếu A’, B’ lần lượt của A và B trên (P).
Bước 2. Nối A’ với B’ ta được đoạn thẳng A’B’ là hình chiếu của đoạn thẳng AB trên mặt phẳng (P).
⦁ Nếu đoạn thẳng AB nằm hoàn toàn trên mặt phẳng (P) thì hình chiếu của đoạn thẳng AB trên mặt phẳng (P) chính là đoạn thẳng AB.
6. Định lý ba đường vuông góc
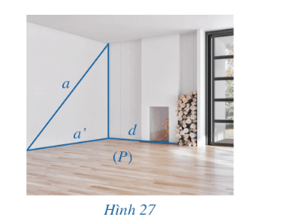
a) Nếu đường thẳng d vuông góc với hình chiếu a’ thì đường thẳng d có vuông góc với a hay không;
b) Ngược lại, nếu đường thẳng d vuông góc với a thì đường thẳng d có vuông góc với hình chiếu a’ hay không.
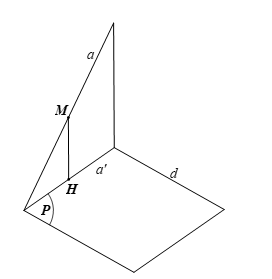
Lời giải:
Lấy điểm M ∈ a, gọi H là hình chiếu của M trên (P).
Khi đó a’ đi qua H vì a’ là hình chiếu của đường thẳng a trên (P).
Ta có: MH ⊥ (P), d ⊂ (P) nên suy ra MH ⊥ d.
a) Ta có: d ⊥ MH, d ⊥ a’ và MH ∩ a’ = H trong mp(a, a’).
Suy ra d ⊥ mp(a, a’).
Mà a ⊂ mp(a, a’) nên d ⊥ a.
Vậy nếu đường thẳng d vuông góc với hình chiếu a’ thì đường thẳng d vuông góc với a.
b) Ta có: d ⊥ MH, d ⊥ a và MH ∩ a = M trong mp(a, a’).
Suy ra d ⊥ mp(a, a’).
Mà a’ ⊂ mp(a, a’) nên d ⊥ a’.
Vậy nếu đường thẳng d vuông góc với a thì đường thẳng d vuông góc với hình chiếu a’.
Lời giải:
Ta có: SA ⊥ (ABCD), BC ⊂ (ABCD) và DC ⊂ (ABCD).
Suy ra: SA ⊥ BC và SA ⊥ DC.
Vì ABCD là hình chữ nhật nên BC ⊥ AB và DC ⊥ AD.
· Ta có: BC ⊥ SA, BC ⊥ AB và SA ∩ AB = A trong (SAB).
Suy ra BC ⊥ (SAB).
Mà SB ⊂ (SAB) nên BC ⊥ SB hay tam giác SBC vuông tại B.
· Ta có: DC ⊥ AD, DC ⊥ SA và AD ∩ SA = A trong (SAD).
Suy ra DC ⊥ (SAD).
Mà SD ⊂ (SAD) nên DC ⊥ SD hay tam giác SCD vuông tại D.
Bài tập
Lời giải:
Quan sát Hình 30 ta thấy a // b, a và b cùng vuông góc với (P). Qua đó, một số các tính chất về quan hệ vuông góc giữa đường thẳng và mặt phẳng được gợi ra như sau:
⦁ Cho hai đường thẳng song song. Một mặt phẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
⦁ Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song với nhau.
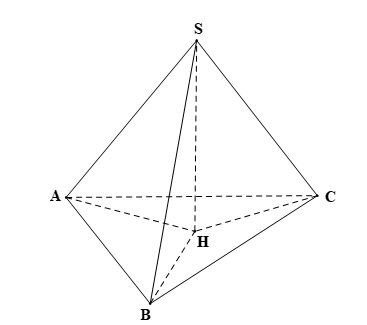
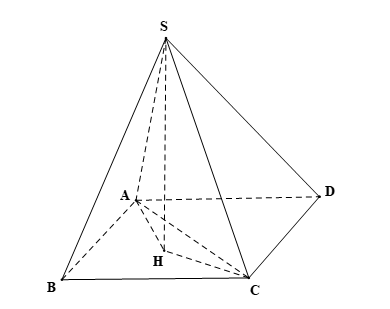
Bài 2 trang 88 Toán 11 Tập 2: Cho hình chóp S.ABC. Gọi H là hình chiếu của S trên mặt phẳng (ABC).
a) Xác định hình chiếu của các đường thẳng SA, SB, SC trên mặt phẳng (ABC).
b) Giả sử BC ⊥ SA, CA ⊥ SB. Chứng minh rằng H là trực tâm của tam giác ABC và AB ⊥ SC.
Lời giải:
a) Ta có: H là hình chiếu của S trên mặt phẳng (ABC); A ∈ (ABC).
Suy ra HA là hình chiếu của SA trên mặt phẳng (ABC).
Tương tự ta có HB, HC lần lượt là hình chiếu của SB và SC trên mặt phẳng (ABC).
b) Do H là hình chiếu của S trên mặt phẳng (ABC) nên SH ⊥ (ABC).
Mà AB, AC, BC đều nằm trên (ABC).
Từ đó ta có: SH ⊥ AB, SH ⊥ AC, SH ⊥ BC.
· Ta có: BC ⊥ SH, BC ⊥ SA và SH ∩ SA = S trong (SAH).
Suy ra BC ⊥ (SAH).
Mà AH ⊂ (SAH) nên BC ⊥ AH. (1)
· Ta có: AC ⊥ SB, AC ⊥ SH và SB ∩ SH = S trong (SBH).
Suy ra AC ⊥ (SBH).
Mà BH ⊂ (SBH) nên AC ⊥ BH. (2)
Từ (1) và (2) ta có H là trực tâm của tam giác ABC.
Suy ra AB ⊥ CH.
· Ta có: AB ⊥ CH, AB ⊥ SH và CH ∩ SH = H trong (SCH).
Suy ra AB ⊥ (SCH).
Mà SC ⊂ (SCH) nên AB ⊥ SC.
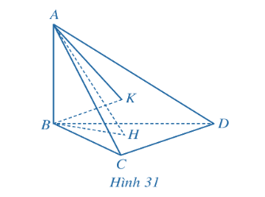
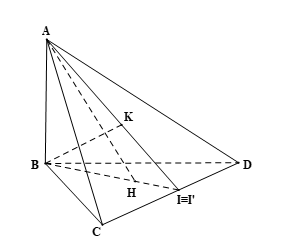
a) CD ⊥ (ABH);
b) CD ⊥ (ABK);
c) Ba đường thẳng AK, BH, CD cùng đi qua một điểm.
Lời giải:
a) Ta có: AB ⊥ (BCD), CD ⊂ (BCD) nên AB ⊥ CD.
Do H là trực tâm của tam giác BCD nên BH ⊥ CD.
Ta có: CD ⊥ AB, CD ⊥ BH và AB ∩ BH = B trong (ABH).
Từ đó ta có: CD ⊥ (ABH).
b) Do K là trực tâm của tam giác ACD nên AK ⊥ CD.
Ta có: CD ⊥ AB, CD ⊥ AK và AB ∩ AK = A trong (ABK).
Từ đó ta có: CD ⊥ (ABK).
c) Theo tính chất “Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước” nên có duy nhất một mặt phẳng đi qua điểm A và vuông góc với CD.
Mà CD ⊥ (ABH), CD ⊥ (ABK).
Suy ra (ABH) ≡ (ABK).
Do: H là trực tâm của tam giác BCD nên BH giao với CD tại một điểm I;
K là trực tâm của tam giác ACD nên AK giao với CD tại một điểm I’.
Mà CD cắt (ABHK) tại một điểm.
Do đó I và I’ trùng nhau hay AK, BH, CD cùng đi qua một điểm.
a) SA ⊥ AD;
b) SC ⊥ CD.
Lời giải:
a) Ta có H là trực tâm của tam giác ABC nên AH ⊥ BC.
Hơn nữa BC // AD (do ABCD là hình bình hành).
Suy ra AH ⊥ AD.
Lại có H là hình chiếu của S trên (ABCD) nên HA là hình chiếu của SA trên (ABCD).
Do đó, theo định lí ba đường vuông góc ta có AD ⊥ SA hay SA ⊥ AD.
b) Ta có H là trực tâm của tam giác ABC nên CH ⊥ AB.
Hơn nữa AB // CD (do ABCD là hình bình hành).
Suy ra HC ⊥ CD.
Lại có H là hình chiếu của S trên (ABCD) nên HC là hình chiếu của SC trên (ABCD).
Do đó, theo định lí ba đường vuông góc ta có CD ⊥ SC hay SC ⊥ CD.
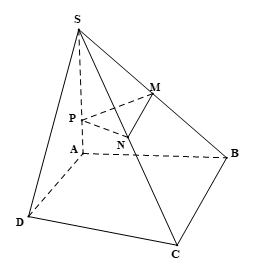
Lời giải:
Do SA ⊥ (ABC) hay SA ⊥ (ABCD) nên AB là hình chiếu của SB trên mặt phẳng (ABCD).
Mà BC ⊥ AB nên theo định lí ba đường vuông góc ta có BC ⊥ SB.
Xét ∆SBC có: M, N lần lượt là trung điểm của SB và SC nên MN là đường trung bình của ∆SBC. Do đó MN // BC.
Mà BC ⊥ SB nên SB ⊥ MN.
Do SA ⊥ (ABCD) và BC ⊂ (ABCD) suy ra SA ⊥ BC.
Mà MN // BC nên SA ⊥ MN.
Ta có: MN ⊥ SB, MN ⊥ SA và SB ∩ SA = S trong (SAB).
Suy ra MN ⊥ (SAB).
Hơn nữa PM ⊂ (SAB) nên MN ⊥ PM hay tam giác MNP là tam giác vuông tại M.
Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác: