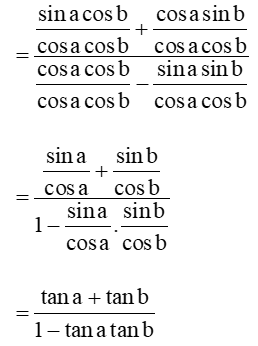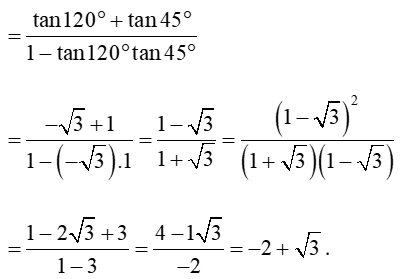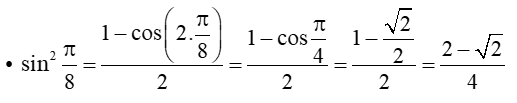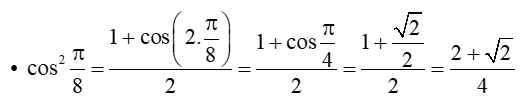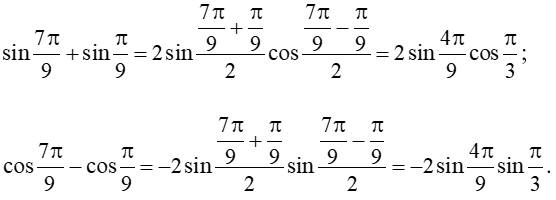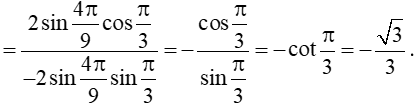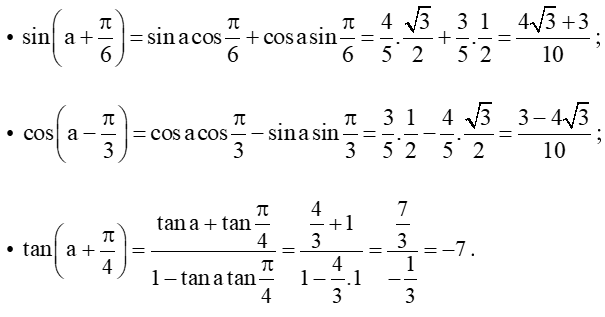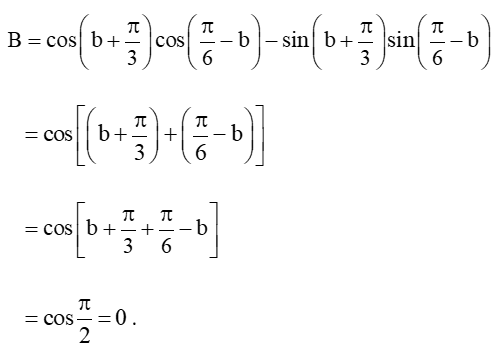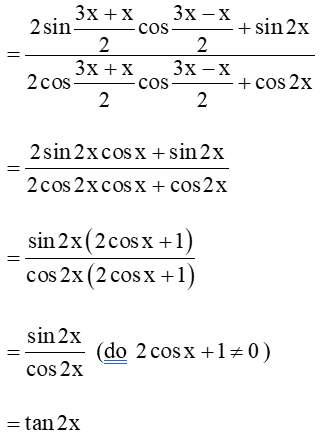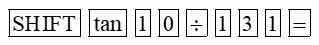Giải SGK Toán 11 (Cánh diều) Bài 2: Các phép biến đổi lượng giác

Giải Toán 11 Bài 2: Các phép biến đổi lượng giác

Câu hỏi khởi động trang 16 Toán 11 Tập 1: Ở lớp dưới, ta đã làm quen với một số phép tính trong tập hợp các số thực, chẳng hạn: phép tính luỹ thừa với số mũ tự nhiên và những công thức để tính toán hay biến đổi những biểu thức chứa các luỹ thừa như vậy. Việc lấy các giá trị lượng giác của góc lượng giác đã hình thành nên những phép tính mới trong tập hợp các số thực, đó là những phép tính lượng giác.

Có hay không những công thức để tính toán hay biến đổi những biểu thức chứa giá trị lượng giác?

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Có các công thức để tính toán hay biến đổi những biểu thức chứa giá trị lượng giác sau:

‒ Công thức cộng;

‒ Công thức nhân đôi;

‒ Công thức biến đổi tích thành tổng;

‒ Công thức biến đổi tổng thành tích.

I. Công thức cộng

Hoạt động 1 trang 16 Toán 11 Tập 1: a) Cho $a=\frac{\pi }{6},b=\frac{\pi }{3}$. Hãy tính sina, cosa, sinb, cosb và sin(a + b). Từ đó rút ra đẳng thức sin(a + b) = sina cosb + cosa sinb (*).

b) Tính sin(a – b) bằng cách biến đổi sin(a – b) = sin[a + (‒b)] và sử dụng công thức (*).

Lời giải:

a) Với $a=\frac{\pi }{6}$ ta có sina = $\sin \frac{\pi }{6}=\frac{1}{2}$; cosa = cos$\frac{\pi }{6}=\frac{\sqrt{3}}{2}$.

Với b=$\frac{\pi }{3}$ ta có sinb = sin$\frac{\pi }{3}=\frac{\sqrt{3}}{2}$; cosb = cos$\frac{\pi }{3}=\frac{1}{2}$.

Ta có sin(a+b) = sin$\left(\frac{\pi }{6}+\frac{\pi }{3}\right)$ = sin$\frac{\pi }{2}$= 1;

sinacosb + cosasinb = $\frac{1}{2}.\frac{1}{2}+\frac{\sqrt{3}}{2}.\frac{\sqrt{3}}{2}=\frac{1}{4}+\frac{3}{4}$= 1

Do đó sin(a + b) = sina cosb + cosa sinb (vì cùng bằng 1).

b) Ta có sin(a – b) = sin[a + (‒b)]

= sina cos(‒b) + cosa sin(‒b)

= sina cosb + cosa (‒sinb)

= sina cosb ‒ cosa sinb

= $\frac{1}{2}.\frac{1}{2}-\frac{\sqrt{3}}{2}.\frac{\sqrt{3}}{2}$

=$\frac{1}{4}-\frac{3}{4}=-\frac{1}{2}$.

Luyện tập 1 trang 16 Toán 11 Tập 1: Tính sin$\frac{\pi }{12}$.

Lời giải:

Áp dụng công thức cộng ta có:

sin$\frac{\pi }{12}$ = sin$\left(\frac{\pi }{3}-\frac{\pi }{4}\right)=\sin \frac{\pi }{3}\cos \frac{\pi }{4}-\cos \frac{\pi }{3}\sin \frac{\pi }{4}$

$=\frac{\sqrt{3}}{2}.\frac{\sqrt{2}}{2}-\frac{1}{2}.\frac{\sqrt{2}}{2}=\frac{\sqrt{6}-\sqrt{2}}{4}$.

Hoạt động 2 trang 17 Toán 11 Tập 1: a) Tính cos(a + b) bằng cách biến đổi cos(a + b) = sin$\left(\frac{\pi }{2}-\left(a+b\right)\right)=\sin \left(\left(\frac{\pi }{2}-a\right)-b\right)$ và sử dụng công thức cộng đối với sin.

b) Tính cos(a ‒ b) bằng cách biến đổi cos(a – b) = cos[a + (‒b)] và sử dụng công thức cos(a + b) có được ở câu a.

Lời giải:

a) Ta có: cos(a + b) = sin$\left(\frac{\pi }{2}-\left(a+b\right)\right)=\sin \left(\left(\frac{\pi }{2}-a\right)-b\right)$

= sin$\left(\frac{\pi }{2}-a\right)$.cosb - cos$\left(\frac{\pi }{2}-a\right)$.sinb

= cosa.cosb - sina.sinb

Vậy cos(a + b) = cosa cosb – sina sinb.

b) Ta có: cos(a – b) = cos[a + (‒b)]

= cosa cos(‒b) – sina sin(‒b)

= cosa cosb ‒ sina (‒sinb)

= cosa cosb + sina sinb.

Vậy cos(a – b) = cosa cosb + sina sinb.

Luyện tập 2 trang 17 Toán 11 Tập 1: Tính cos15°.

Lời giải:

Áp dụng công thức cộng, ta có:

cos15° = cos(45° ‒ 30°)

= cos45°.cos30° + sin45°.sin30°

= $\frac{\sqrt{2}}{2}.\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}.\frac{1}{2}=\frac{\sqrt{6}+\sqrt{2}}{4}$.

Hoạt động 3 trang 17 Toán 11 Tập 1: a) Sử dụng công thức cộng đối với sin và côsin, hãy tính tan(a + b) theo tana và tanb khi các biểu thức đều có nghĩa.

b) Khi các biểu thức đều có nghĩa, hãy tính tan (a – b) bằng cách biến đổi tan(a-b) = tan[a+(-b)] và sử dụng công thức tan(a + b) có được ở câu a.

Lời giải:

a) Khi các biểu thức đều có nghĩa, ta có:

tan(a + b) = $\frac{\sin \left(a+b\right)}{cos\left(a+b\right)}=\frac{\sin a\cos b+\cos a\sin b}{\cos a\cos b-\sin a\sin b}$

 (chia cả tử và mẫu cho cosacosb)

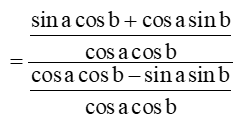
Vậy tan(a+b) = $\frac{\tan a+\tan b}{1-\tan a\tan b}$.

b) Khi các biểu thức đều có nghĩa, ta có:

tan(a-b) = tan[a+(-b)]

$=\frac{\tan a+\tan \left(-b\right)}{1-\tan a\tan \left(-b\right)}$

$=\frac{\tan a-\tan b}{1+\tan a\tan b}$ .

Vậy tan(a-b) = $\tan \left(a-b\right)=\frac{\tan a-\tan b}{1+\tan a\tan b}$.

Luyện tập 3 trang 17 Toán 11 Tập 1: Tính tan165°.

Lời giải:

Áp dụng công thức cộng, ta có:

tan165° = tan(120° + 45°)

Vậy tan165^o = -2+$\sqrt{3}$.

II. Công thức nhân đôi

Hoạt động 4 trang 18 Toán 11 Tập 1: Tính sin2a, cos2a, tan2a bằng cách thay b = a trong công thức cộng.

Lời giải:

Ta có:

• sin2a = sin(a + a) = sinacosa + cosasina = 2sinacosa;

• cos2a = cos(a + a) = cosacosa – sinasina = cos²a – sin²a;

• Khi các biểu thức đều có nghĩa thì

tan2a = tan(a+a) = $\frac{\tan a+\tan a}{1-\tan a\tan a}=\frac{2\tan a}{1-{\tan }^{2}a}$ .

Luyện tập 4 trang 18 Toán 11 Tập 1: Cho tan$\frac{a}{2}$ = -2. Tính tana.

Lời giải:

Áp dụng công thức nhân đôi, ta có:

tana = $\frac{2\tan \frac{a}{2}}{1-{\tan }^2\frac{a}{2}}=\frac{2.\left(-2\right)}{1-{\left(-2\right)}^2}=\frac{-4}{-3}=\frac{4}{3}$.

Luyện tập 5 trang 18 Toán 11 Tập 1: Tính: sin$\frac{\pi }{8}$, cos$\frac{\pi }{8}$.

Lời giải:

Áp dụng công thức hạ bậc, ta có:

Mà sin$\frac{\pi }{8}$>0 nên sin$\frac{\pi }{8}$= $\sqrt{\frac{2-\sqrt{2}}{4}}=\frac{\sqrt{2-\sqrt{2}}}{2}$.

Mà cos$\frac{\pi }{8}$>0 nên cos$\frac{\pi }{8}=\sqrt{\frac{2+\sqrt{2}}{4}}=\frac{\sqrt{2+\sqrt{2}}}{2}$.

III. Công thức biến đổi tích thành tổng

Hoạt động 5 trang 18 Toán 11 Tập 1: Sử dụng công thức cộng, rút gọn mỗi biểu thức sau:

cos(a + b) + cos(a – b); cos(a + b) – cos(a – b); sin(a + b) + sin(a – b).

Lời giải:

Ta có:

• cos(a + b) + cos(a – b)

= (cosa cosb – sina sinb) + (cosa cosb + sina sinb)

= cosa cosb – sina sinb + cosa cosb + sina sinb

= 2cosa cosb.

• cos(a + b) – cos(a – b)

= (cosa cosb – sina sinb) – (cosa cosb + sina sinb)

= cosa cosb – sina sinb – cosa cosb – sina sinb

= –2sina sinb.

• sin(a + b) + sin(a – b)

= (sina cosb + cosa sinb) + (sina cosb ‒ cosa sinb)

= sina cosb + cosa sinb + sina cosb ‒ cosa sinb

= 2sina cosb.

Vậy cos(a + b) + cos(a – b) = 2cosa cosb;

cos(a + b) – cos(a – b) = –2sina sinb;

sin(a + b) + sin(a – b) = 2sina cosb.

Luyện tập 6 trang 19 Toán 11 Tập 1: Cho cosa = $\frac{2}{3}$. Tính B = cos$\frac{3a}{2}$cos$\frac{a}{2}$.

Lời giải:

Áp dụng công thức biến đổi tích thành tổng, ta có:

B = cos$\frac{3a}{2}$cos$\frac{a}{2}$

$=\frac{1}{2}\left(\cos \left(\frac{3a}{2}+\frac{a}{2}\right)+\cos \left(\frac{3a}{2}-\frac{a}{2}\right)\right)$

$=\frac{1}{2}\left(\cos 2a+\cos a\right)$

Mà cos2a = 2cos²a – 1 = $2.{\left(\frac{2}{3}\right)}^2-1=2.\frac{4}{9}-1=-\frac{1}{9}$

Do đó B = $\frac{1}{2}$[cos2a + cosa] = $\frac{1}{2}.\left(-\frac{1}{9}+\frac{2}{3}\right)=\frac{5}{18}$.

IV. Công thức biến đổi tổng thành tích

Hoạt động 6 trang 19 Toán 11 Tập 1: Sử dụng công thức biến đổi tích thành tổng và đặt a + b = u; a − b = v rồi biến đổi các biểu thức sau thành tích: cosu + cosv; cosu – cos v; sinu + sinv; sinu – sinv.

Lời giải:

Ta có 

Khi đó:

• cosu + cosv = cos(a + b) + cos(a – b)

= 2cosa cosb

= 2cos$\frac{u+v}{2}\cos \frac{u-v}{2}$.

• cosu – cosv = cos(a + b) – cos(a – b)

= –2sina sinb

= -2sin$\frac{u+v}{2}\sin \frac{u-v}{2}$.

• sinu + sinv = sin(a + b) + sin(a – b)

= 2sina cosb

= 2sin$\frac{u+v}{2}\cos \frac{u-v}{2}$.

• sinu – sinv = sin(a + b) – sin(a – b)

= sin(b + a) + sin(b – a)

= 2sinb cosa = 2cosa sinb

= 2cos$\frac{u+v}{2}\sin \frac{u-v}{2}$.

Luyện tập 7 trang 19 Toán 11 Tập 1: Tính: D = $\frac{\sin \frac{7\pi }{9}+\sin \frac{\pi }{9}}{\text{cos}\frac{7\pi }{9}-\cos \frac{\pi }{9}}$.

Lời giải:

Áp dụng công thức biến đổi tổng thành tích ta có:

Khi đó:

D = $\frac{\sin \frac{7\pi }{9}+\sin \frac{\pi }{9}}{\text{cos}\frac{7\pi }{9}-\cos \frac{\pi }{9}}$

Bài tập

Bài 1 trang 20 Toán 11 Tập 1: Cho cosa = $\frac{3}{5}$ với 0$\frac{\pi }{2}$. Tính sin$\left(a+\frac{\pi }{6}\right)$, cos$\left(a-\frac{\pi }{3}\right)$, tan$\left(a+\frac{\pi }{4}\right)$.

Lời giải:

Do 0$\frac{\pi }{2}$ nên sina>0.

Áp dụng công thức sin²a + cos²a = 1, ta có:

$si{n}^{2}a+{\left(\frac{3}{5}\right)}^2=1$

$\Rightarrow si{n}^{2}a=1-{\left(\frac{3}{5}\right)}^2=1-\frac{9}{25}=\frac{16}{25}$

$\Rightarrow$sina = $\frac{4}{5}$ (do sina > 0).

Khi đó tana = $\frac{\sin a}{\cos a}=\frac{\frac{4}{5}}{\frac{3}{5}}=\frac{4}{3}$.

Áp dụng công thức cộng, ta có:

Bài 2 trang 20 Toán 11 Tập 1: Tính:

A = sin(a – 17°)cos(a + 13°) – sin(a + 13°)cos(a – 17°);

B = cos$\left(b+\frac{\pi }{3}\right)$cos$\left(\frac{\pi }{6}-b\right)$ - sin$\left(b+\frac{\pi }{3}\right)$sin$\left(\frac{\pi }{6}-b\right)$.

Lời giải:

Ta có:

A = sin(a – 17°)cos(a + 13°) – sin(a + 13°)cos(a – 17°)

= sin(a – 17°)cos(a + 13°) – cos(a – 17°)sin(a + 13°)

= sin[(a – 17°) – (a + 13°)]

= sin(a – 17° – a – 13°)

= sin(‒30°)

= ‒ sin30°

=-$\frac{1}{2}$ .

Bài 3 trang 20 Toán 11 Tập 1: Cho tan(a + b) = 3, tan(a – b) = 2. Tính: tan2a, tan2b.

Lời giải:

Ta có:

tan2a = tan[(a + b) + (a – b)]

$=\frac{\tan \left(a+b\right)+\tan \left(a-b\right)}{1-\tan \left(a+b\right)\tan \left(a-b\right)}=\frac{3+2}{1-3.2}=\frac{5}{-5}=-1$;

tan2b = tan[(a + b) ‒ (a – b)]

$=\frac{\tan \left(a+b\right)-\tan \left(a-b\right)}{1+\tan \left(a+b\right)\tan \left(a-b\right)}=\frac{3-2}{1+3.2}=\frac{1}{7}$.

Bài 4 trang 20 Toán 11 Tập 1: Cho sina = $\frac{2}{\sqrt{5}}$. Tính cos2a, cos4a.

Lời giải:

Áp dụng công thức hạ bậc, ta có:

cos2a = 1 – 2sin²a = 1 -2.${\left(\frac{2}{\sqrt{5}}\right)}^2=1-2.\frac{4}{5}=-\frac{3}{5}$.

cos4a = 2cos²a – 1 = ${\left(-\frac{3}{5}\right)}^2-1=\frac{9}{25}-1=-\frac{16}{25}$.

Bài 5 trang 20 Toán 11 Tập 1: Cho sina + cosa = 1. Tính: sin2a.

Lời giải:

Ta có: sina + cosa = 1

$\Rightarrow$ (sina + cosa)² = 1²

$\Rightarrow$ sin²a + 2sina cosa + cos²a = 1

$\Rightarrow$ 2sina cosa + (sin²a + cos²a) = 1

$\Rightarrow$ sin2a + 1 = 1

$\Rightarrow$ sin2a = 0.

Vậy với sina + cosa = 1 thì sin2a = 0.

Bài 6 trang 21 Toán 11 Tập 1: Cho cos2a = $\frac{1}{3}$ với $\frac{\pi }{2}$$\pi$. Tính: sina, cosa, tana.

Lời giải:

Do $\frac{\pi }{2}$$\pi$ nên cosa < 0 và sina > 0.

Áp dụng công thức hạ bậc ta có:

• sin²a = $\frac{1-\cos 2a}{2}=\frac{1-\frac{1}{3}}{2}=\frac{1}{3}$$\Rightarrow$sina = $\frac{\sqrt{3}}{3}$ (do sina > 0).

• cos²a = $\frac{1+\cos 2a}{2}=\frac{1+\frac{1}{3}}{2}=\frac{2}{3}$ $\Rightarrow$ cosa = $-\frac{\sqrt{6}}{3}$(do cosa < 0).

Khi đó: tana = $\frac{\sin a}{\cos a}=\frac{\frac{\sqrt{3}}{3}}{-\frac{\sqrt{6}}{3}}=\frac{\sqrt{2}}{2}$.

Vậy sina = $\frac{\sqrt{3}}{3}$, cosa = $-\frac{\sqrt{6}}{3}$ và tana = $\frac{\sqrt{2}}{2}$.

Bài 7 trang 21 Toán 11 Tập 1: Cho cos2x = $\frac{1}{4}$. Tính: A = cos$\left(x+\frac{\pi }{6}\right)$cos$\left(x-\frac{\pi }{6}\right)$; B = sin$\left(x+\frac{\pi }{3}\right)$sin$\left(x-\frac{\pi }{3}\right)$.

Lời giải:

Ta có:

A = cos$\left(x+\frac{\pi }{6}\right)$cos$\left(x-\frac{\pi }{6}\right)$

$=\frac{1}{2}\left(\cos \left(x+\frac{\pi }{6}+x-\frac{\pi }{6}\right)+\cos \left(x+\frac{\pi }{6}-x+\frac{\pi }{6}\right)\right)$

$=\frac{1}{2}\left(\cos 2x+\cos \frac{\pi }{3}\right)$

$=\frac{1}{2}\left(\frac{1}{4}+\frac{1}{2}\right)=\frac{3}{8}$.

B = sin$\left(x+\frac{\pi }{3}\right)$sin$\left(x-\frac{\pi }{3}\right)$

$=-\frac{1}{2}\left(\cos \left(x+\frac{\pi }{3}+x-\frac{\pi }{3}\right)-\cos \left(x+\frac{\pi }{3}-x+\frac{\pi }{3}\right)\right)$

$=-\frac{1}{2}\left(\cos 2x-\cos \frac{2\pi }{3}\right)$

$=-\frac{1}{2}\left(\frac{1}{4}-\left(-\frac{1}{2}\right)\right)=-\frac{3}{8}$.

Vậy A = $\frac{3}{8}$, B = -$\frac{3}{8}$.

Bài 8 trang 21 Toán 11 Tập 1: Rút gọn biểu thức: A = $\frac{\sin x+\sin 2x+\sin 3x}{\cos x+\cos 2x+\cos 3x}$.

Lời giải:

Khi các biểu thức đều có nghĩa, ta có:

A = $\frac{\sin x+\sin 2x+\sin 3x}{\cos x+\cos 2x+\cos 3x}$

$=\frac{\left(\sin 3x+\sin x\right)+\sin 2x}{\left(\cos 3x+\cos x\right)+\cos 2x}$

Bài 9 trang 21 Toán 11 Tập 1: Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14 m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12 m. Biết rằng hai sợi cáp trên cùng được gắn với mặt đất tại một vị trí cách chân cột 15 m (Hình 17).

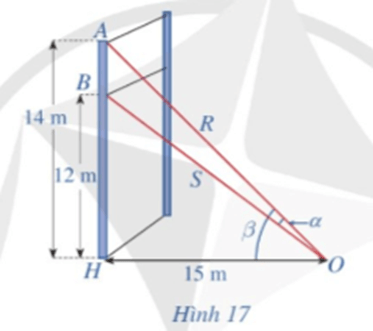
a) Tính tanα, ở đó α là góc giữa hai sợi cáp trên.

b) Tìm góc α (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).

Lời giải:

a) Xét DAOH vuông tại H, ta có: tan$\beta =\frac{AH}{HO}=\frac{14}{15}$.

Đặt $\widehat{BOH}=\gamma$

Xét DBOH vuông tại H, ta có: tan$\gamma =\frac{BH}{HO}=\frac{12}{15}=\frac{4}{5}$.

tan$\alpha$ = tan($\beta -\widehat{BOH}$) = tan$\left(\beta -\gamma \right)=\frac{\tan \beta -\tan \gamma }{1+\tan \beta \tan \gamma }$

$=\frac{\frac{14}{15}-\frac{4}{5}}{1+\frac{14}{15}.\frac{4}{5}}=\frac{\frac{2}{15}}{\frac{131}{75}}=\frac{10}{131}$.

Vậy tan$\alpha =\frac{10}{131}$.

b) Từ tan$\alpha =\frac{10}{131}$, để tìm số đo góc α, ta sử dụng máy tính cầm tay ấn lần lượt các nút:

Ta được kết quả làm tròn kết quả đến hàng đơn vị theo đơn vị độ là 4°.

Vậy α ≈ 4°.

Bài 10 trang 21 Toán 11 Tập 1: Có hai chung cư cao tầng xây cạnh nhau với khoảng cách giữa chúng là HK = 20 m. Để đảm bảo an ninh, trên nóc chung cư thứ hai người ta lắp camera ở vị trí C. Gọi A, B lần lượt là vị trí thấp nhất, cao nhất trên chung cư thứ nhất mà camera có thể quan sát được (Hình 18). Hãy tính số đo góc ACB (phạm vi camera có thể quan sát được ở chung cư thứ nhất). Biết rằng chiều cao của chung cư thứ hai là CK = 32 m, AH = 6 m, BH = 24 m (làm tròn kết quả đến hàng phần mười theo đơn vị độ).

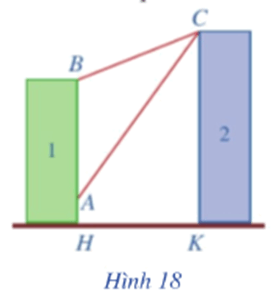
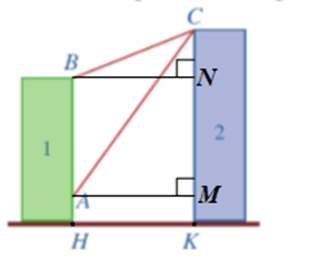
Lời giải:

Kẻ AM ⊥ CK, BN ⊥CK (hình vẽ) ta có:

BN = AM = HK = 20 (m);

CN = CK – NK = CK – BH = 32 – 24 = 8 (m);

MN = AB = BH – AH = 24 – 6 = 18 (m);

CM = CN + MN = 8 + 18 = 26 (m).

Đặt $\widehat{BCN}=\alpha ,\widehat{ACM}=\beta$.

Xét $∆$BCN vuông tại N có: tan$\alpha =\frac{BN}{CN}=\frac{20}{8}=\frac{5}{2}$;

Xét $∆$ACM vuông tại M có: tan$\beta =\frac{AM}{CM}=\frac{20}{26}=\frac{10}{13}$;

Ta có: tan$\widehat{ACB}=\tan \left(\widehat{BCN}-\widehat{ACM}\right)=\tan \left(\alpha -\beta \right)$

$\Rightarrow \tan \widehat{ACB}=\frac{\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta }=\frac{\frac{5}{2}-\frac{10}{13}}{1+\frac{5}{2}.\frac{10}{13}}=\frac{45}{76}$.

$\Rightarrow \widehat{ACB}\approx 0,01°$.

Vậy góc ACB (phạm vi camera có thể quan sát được ở chung cư thứ nhất) có số đo xấp xỉ 0,01°.