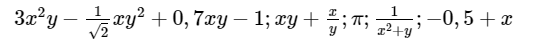Giải SBT Toán 8 (Kết nối tri thức) Bài 2: Đa thức
Bài 1.7 trang 9 SBT Toán 8 Tập 1: Những biểu thức nào sau đây là đa thức:
Lời giải:
Các biểu thức là đa thức là:
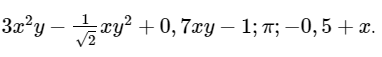
Bài 1.8 trang 9 SBT Toán 8 Tập 1: Cho đa thức M = x3 – 2xy + 3xyz – 4xy2 + 5x2y – 6xyz + 7xy2 – 8xy.
b) Tìm các hạng tử bậc 3 trong dạng thu gọn của M.
Lời giải:
a) Thu gọn M ta có:
M = x3 ‒ 2xy + 3xyz ‒ 4xy2 + 5x2y ‒ 6xyz + 7xy2 ‒ 8xy
= x3 + (‒2xy ‒ 8xy) + (3xyz ‒ 6xyz) + (‒ 4xy2 + 7xy2) + 5x2y
= x3 ‒ 10xy ‒ 3xyz +3xy2 + 5x2y.
b) Các hạng tử bậc 3 là x3; –3xyz; 3xy2 và 5x2y.
Lời giải:
Các đơn thức chứa biến x, y có hệ số bằng 1 và có bậc 2 là: x2; xy; y2.
Vậy đa thức P thu gọn với hai biến x và y cần tìm là: P = x2 + xy + y2.
Lời giải:
Các đơn thức chứa biến x, y, z có hệ số bằng 1 và có bậc 3 là:
x3; y3; z3; x2y; xy2; x2z; xz2; y2z; yz2; xyz.
Vậy đa thức Q thu gọn với ba biến x, y, z cần tìm là:
Q = x3 + y3 + z3 + x2y + xy2 + x2z + xz2 + y2z + yz2 + xyz.
Bài 1.11 trang 9 SBT Toán 8 Tập 1: Cho đa thức N = 1,5x3y2 – 3xyz + 2x2y – 1,5x3y2 + xy2z + 2,5xyz.
b) Tính giá trị của N tại x = 2; y = –2; z = 3.
Lời giải:
a) Thu gọn đa thức N ta có:
N = 1,5x3y2 – 3xyz + 2x2y – 1,5x3y2 + xy2z + 2,5xyz
= (1,5x3y2– 1,5x3y2) + (– 3xyz+ 2,5xyz) + 2x2y + xy2z
= ‒0,5xyz + 2x2y + xy2z.
Vậy N là đa thức bậc 4.
b) Tại x = 2; y = –2; z = 3 ta có:
N = ‒0,5.2.(‒2).3 + 2.22.(‒2) + 2.(‒2)2.3 = 6 ‒ 16 + 24 = 14.
Bài 1.12 trang 9 SBT Toán 8 Tập 1: Tìm bậc của mỗi đa thức sau:
a) 5x4 – 3x3y + 2xy3 – x3y + 2y4 – 6x2y2 – 2xy3;
Lời giải:
a) Thu gọn đa thức ta có:
5x4 – 3x3y + 2xy3 – x3y + 2y4 – 6x2y2 – 2xy3
= 5x4+ 2y4 + (– 3x3y– x3y) + (2xy3– 2xy3) – 6x2y2
= 5x4+ 2y4 ‒ 4x3y– 6x2y2.
Vậy đây là đa thức bậc 4.
b) Thu gọn đa thức ta có:
= yz3 +0,25y4 ‒ 5.
Vậy đây là đa thức bậc 4.
Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
Bài 3: Phép cộng và phép trừ đa thức