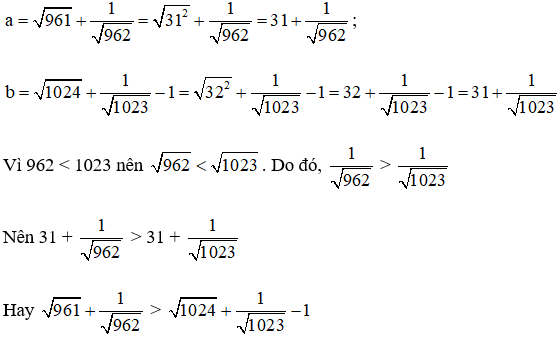Giải SBT Toán 7 (Kết nối tri thức) Bài 6: Số vô tỉ. Căn bậc hai số học

Giải Sách bài tập Toán lớp 7 Bài 6: Số vô tỉ. Căn bậc hai số học

Giải trang 28 Tập 1

Bài 2.10 trang 28 sách bài tập Toán lớp 7 Tập 1:Những số nào sau đây có căn bậc hai số học?

0,9; -4; 11; -100; $\frac{4}{5};\pi$.

Lời giải:

Những số không âm là những số có căn bậc hai số học.

Do đó 0,9; 11; $\frac{4}{5};\pi$ là những số có căn bậc hai số học.

Bài 2.11 trang 28 sách bài tập Toán lớp 7 Tập 1:Trong các kết quả sau, kết quả nào đúng?

A. $\sqrt{0,1}=0,01$;

B. $\sqrt{16}=-4$;

C. $\sqrt{-0,09}=0,3$;

D. $\sqrt{0,04}=0,2$

Lời giải:

Ta có: $\sqrt{0,1}=0,01$ đây là kết quả sai vì $\sqrt{0,1}=0,\mathrm{31622...}$

$\sqrt{16}=-4$ đây là kết quả sai vì $\sqrt{16}=4$.

$\sqrt{-0,09}=0,3$ đây là kết quả sai vì -0,09 không có căn bậc hai số học.

$\sqrt{0,04}=0,2$ đây là kết quả đúng vì 0,2² = 0,04.

Bài 2.12 trang 28 sách bài tập Toán lớp 7 Tập 1: Những biểu thức nào dưới đây có giá trị bằng $\frac{3}{7}$?

$\sqrt{\frac{3^2}{7^2}};$ $\frac{\sqrt{3^2}+\sqrt{{39}^2}}{\sqrt{7^2}+\sqrt{{91}^2}}$;

$\frac{39}{91}$; $\frac{\sqrt{3^2}-\sqrt{{39}^2}}{\sqrt{7^2}-\sqrt{{91}^2}}$

Lời giải:

$\sqrt{\frac{3^2}{7^2}}=\sqrt{\frac{9}{49}}=\sqrt{{\left(\frac{3}{7}\right)}^2}=\frac{3}{7}$;

$\frac{\sqrt{3^2}+\sqrt{{39}^2}}{\sqrt{7^2}+\sqrt{{91}^2}}=\frac{3+39}{7+91}=\frac{42}{98}=\frac{3}{7}$;

$\frac{39}{91}=\frac{39:13}{91:13}=\frac{3}{7}$

$\frac{\sqrt{3^2}-\sqrt{{39}^2}}{\sqrt{7^2}-\sqrt{{91}^2}}=\frac{3-39}{7-91}=\frac{-36}{-84}=\frac{3}{7}$

Vậy tất cả các biểu thức đã cho đều có giá trị bằng $\frac{3}{7}$.

Bài 2.13 trang 28 sách bài tập Toán lớp 7 Tập 1: Số nào trong các số:

$-\frac{16}{3};\sqrt{36};\sqrt{47};-2\pi ;\sqrt{0,01};2+\sqrt{7}$ là số vô tỉ?

Lời giải:

$-\frac{16}{3}$ = -5,(3). Vì $-\frac{16}{3}$ được viết dưới dạng số thập phân vô hạn tuần hoàn nên $-\frac{16}{3}$ không phải số vô tỉ.

$\sqrt{36}$ = 6. Vì $\sqrt{36}$ là số nguyên nên $\sqrt{36}$ không phải số vô tỉ.

$\sqrt{47}$ = 6,855... Vì $\sqrt{47}$ được viết dưới dạng số thập phân vô hạn không tuần hoàn nên $\sqrt{47}$ là số vô tỉ.

-2π = -6,2831… Vì -2π được viết dưới dạng số thập phân vô hạn không tuần hoàn nên -2π là số vô tỉ.

$\sqrt{0,01}$ = 0,1. Vì $\sqrt{0,01}$ được viết dưới dạng số thập phân hữu hạn nên $\sqrt{0,01}$ không là số vô tỉ.

2 + $\sqrt{7}$ = 4,645… Vì 2 + $\sqrt{7}$ được viết dưới dạng số thập phân vô hạn không tuần hoàn nên 2 + $\sqrt{7}$ là số vô tỉ.

Vậy các số vô tỉ là $\sqrt{47}$; -2π; 2 + $\sqrt{7}$.

Bài 2.14 trang 28 sách bài tập Toán lớp 7 Tập 1:Số nào trong các số sau là số vô tỉ?

a = 0,777…; b = 0,70700700070000…;

c = $\frac{-1}{7}$; d = $\sqrt{{\left(-7\right)}^2}$

Lời giải:

a = 0,777… = 0,(7). Vì a được viết dưới dạng số thập phân vô hạn tuần hoàn nên a không là số vô tỉ;

b = 0,70700700070000… Vì b được viết dưới dạng số thập phân vô hạn không tuần hoàn nên b là số vô tỉ;

c = $\frac{-1}{7}$ = -0,142857142857... = -0,(142857). Vì c được viết dưới dạng số thập phân vô hạn tuần hoàn nên c không là số vô tỉ;

d = $\sqrt{{\left(-7\right)}^2}$ = $\sqrt{49}$ = 7. Vì d là số nguyên nên d không là số vô tỉ.

Vậy trong các số đã cho chỉ có số 0,70700700070000… là số vô tỉ.

Bài 2.15 trang 28 sách bài tập Toán lớp 7 Tập 1:Tìm căn bậc hai số học của các số sau: 81; 8 100; 0,81; 81².

Lời giải:

$\sqrt{81}=\sqrt{9^2}=9$;

$\sqrt{8100}=\sqrt{{90}^2}=90$;

$\sqrt{0,81}=\sqrt{0,9^2}=0,9$;

$\sqrt{{81}^2}=81$.

Bài 2.16 trang 28 sách bài tập Toán lớp 7 Tập 1:Cho $a=\sqrt{961}+\frac{1}{\sqrt{962}}$ và b = $\sqrt{1024}+\frac{1}{\sqrt{1023}}-1$. So sánh a và b.

Lời giải:

Vậy a > b.

Bài 2.17 trang 28 sách bài tập Toán lớp 7 Tập 1:Xét số a = 1 + $\sqrt{2}$.

a) Làm tròn số a đến hàng phần trăm;

b) Làm tròn số a đến chữ số thập phân thứ năm;

c) Làm tròn số a với độ chính xác 0,0005.

Lời giải:

a = 1 + $\sqrt{2}$ = 2,414213562…

a) Ta gạch chân dưới chữ số hàng phần trăm 2,414213562…

Nhận thấy chữ số bên phải liền kề hàng phần trăm là 4 < 5 nên ta giữ nguyên chữ số hàng phần trăm và bỏ đi các chữ phần thập phân phía sau hàng phân trăm.

Vậy làm tròn số 1 + $\sqrt{2}$ đến hàng phần trăm ta thu được kết quả là 2,41.

b) Ta gạch chân dưới chữ số thập phân thứ năm 2,414213562…

Nhận thấy chữ số bên phải liền kề chữ số thập phân thứ năm là 3 < 5 nên ta giữ nguyên chữ số thập phân thứ năm và bỏ đi các chữ phần thập phân phía sau chữ số thập phân thứ 5.

Vậy làm tròn số 1 + $\sqrt{2}$ đến chữ số thập phân thứ năm ta thu được kết quả là 2,41421.

c) Làm tròn số a với độ chính xác 0,0005 tức là ta làm tròn số đó đến hàng phần nghìn.

Ta gạch chân dưới chữ số hàng phần nghìn 2,414213562…

Nhận thấy chữ số bên phải liền kề chữ số hàng phần nghìn là 2 < 5 nên ta giữ nguyên chữ số hàng phần nghìn và bỏ đi các chữ phần thập phân phía sau chữ số hàng phân nghìn.

Vậy làm tròn số 1 + $\sqrt{2}$ đến chữ số hàng phần nghìn ta thu được kết quả là 2,414.

Bài 2.18 trang 28 sách bài tập Toán lớp 7 Tập 1: Biểu thức $\sqrt{x+8}-7$ có giá trị nhỏ nhất bằng:

A. $\sqrt{8}-7$;

B. – 7;

C. 0;

D. $\sqrt{-8}-7$.

Lời giải:

Điều kiện: x + 8 ≥ 0 nên x ≥ -8

Vì $\sqrt{x+8}$ ≥ 0 với mọi x ≥ -8

Nên $\sqrt{x+8}-7\ge 0-7$.

Do đó, $\sqrt{x+8}-7\ge -7$

Vậy giá trị nhỏ nhất của $\sqrt{x+8}-7$ là -7. Dấu “=” xảy ra khi x + 8 = 0 hay x = -8.

Bài 2.19 trang 28 sách bài tập Toán lớp 7 Tập 1:Giá trị lớn nhất của biểu thức $3-\sqrt{x-6}$ bằng:

A. $3-\sqrt{6}$

B. $3-\sqrt{-6}$

C. $3+\sqrt{6}$

D. 3

Lời giải:

Điều kiện: x – 6 ≥ 0 nên x ≥ 6

Vì $\sqrt{x-6}$ ≥ 0 nên $-\sqrt{x-6}\le 0$ với mọi x ≥ 6

Nên $3+\text{}\left(-\sqrt{x-6}\right)\le 3+0$ hay $3-\sqrt{x-6}\le 3+0$.

Do đó, $3-\sqrt{x-6}\le 3$

Vậy giá trị lớn nhất của $3-\sqrt{x-6}$ là 3. Dấu “=” xảy ra khi x – 6 = 0 hay x = 6.

Bài 2.20 trang 28 sách bài tập Toán lớp 7 Tập 1:Tìm giá trị lớn nhất của biểu thức: $\frac{4}{3+\sqrt{2-x}}$

Lời giải:

Điều kiện: 2 – x ≥ 0 nên x ≤ 2.

Ta có: $\sqrt{2-x}\ge 0$ với mọi x ≤ 2

Nên $3+\sqrt{2-x}\ge 3+0$ hay $3+\sqrt{2-x}\ge 3$.

Do đó, $\frac{4}{3+\sqrt{2-x}}\le \frac{4}{3}$

Vậy giá trị lớn nhất của $\frac{4}{3+\sqrt{2-x}}$ là $\frac{4}{3}$. Dấu “=” xảy ra khi $3+\sqrt{2-x}=3$ hay $\sqrt{2-x}=0$ nên x = 2. Do đó, $\frac{4}{3+\sqrt{2-x}}$ có giá trị lớn nhất là $\frac{4}{3}$ khi x = 2.

Bài 2.21 trang 28 sách bài tập Toán lớp 7 Tập 1:Tìm số tự nhiên n nhỏ hơn 45 sao cho $x=\frac{\sqrt{n}-1}{2}$ là số nguyên.

Lời giải:

Vì $x=\frac{\sqrt{n}-1}{2}$ là số nguyên nên $\sqrt{n}-1$ phải chia hết cho 2 và $\sqrt{n}$ cũng là số nguyên hay n là các số chính phương. Mà n < 45 nên ta có các số chính phương nhỏ hơn 45 là {0; 1; 4; 9; 16; 25; 36}.

Vì $\sqrt{n}-1$ chia hết cho 2 nên $\sqrt{n}$ là số lẻ nên n lẻ. Do đó, n ∈ {1; 9; 25}

Vậy để $x=\frac{\sqrt{n}-1}{2}$ là số nguyên thì n ∈ {1; 9; 25}.

Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 4: Thứ tự thực hiện các phép tính. Quy tắc chuyển vế

Bài 5: Làm quen với số thập phân vô hạn tuần hoàn

Bài 7: Tập hợp các số thực

Ôn tập chương 2

Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc