Giải SBT Toán 7 (Kết nối tri thức) Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc

Giải Sách bài tập Toán lớp 7 Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc

Giải trang 36 Tập 1

Bài 3.1 trang 36 Tập 1: Cho Hình 3.4, kể tên các cặp góc kề bù.

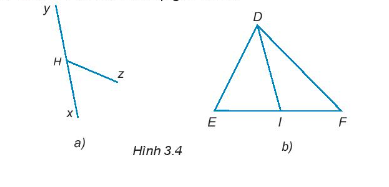
Lời giải:

Các cặp góc kề bù có trong hình là:

Hình 3.4a: $\widehat{xHz}$ và $\widehat{yHz}$

Hình 3.4b: $\widehat{EID}$ và $\widehat{FID}$.

Giải trang 37 Tập 1

Bài 3.2 trang 37 Tập 1: Cho Hình 3.5

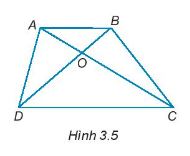
a) Gọi tên các cặp góc đối đỉnh.

b) Gọi tên góc kề bù với $\widehat{AOD}$.

Lời giải:

a) Các cặp góc đối đỉnh là: $\widehat{AOB}$ và $\widehat{DOC}$;  $\widehat{AOD}$ và $\widehat{BOC}$.

b) Góc kề bù với góc $\widehat{AOD}$ là góc $\widehat{AOB}$ và $\widehat{COD}$.

Bài 3.3 trang 37 Tập 1: Vẽ hai đường thẳng xy và mn cắt nhau tại điểm O sao cho $\widehat{xOm}=120°$. Tính các góc $\widehat{mOy};\widehat{yOn};\widehat{xOn}$.

Lời giải:

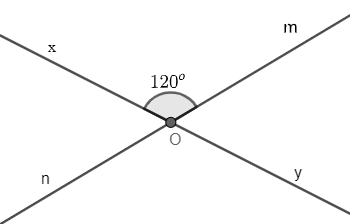
Vì góc $\widehat{xOm}$ và góc $\widehat{nOy}$ là hai góc đối đỉnh nên $\widehat{xOm}=\widehat{nOy}=120°$ 

Vì góc $\widehat{xOn}$ và góc $\widehat{nOy}$ là hai góc kề bù nên $\widehat{xOn}$ + $\widehat{xOm}=180°$

$\widehat{xOn}$ + $120°=180°$

$\widehat{xOn}$ = 180^o – 120^o

$\widehat{xOn}$ = 60^o.

Mà $\widehat{xOn}$ và $\widehat{yOm}$ đối đỉnh nên $\widehat{xOn}$ = $\widehat{yOm}$ = 60^o.

Bài 3.4 trang 37 Tập 1: Vẽ $\widehat{xAm}=50°$. Vẽ tia phân giác An của $\widehat{xAm}$.

a) Tính $\widehat{xAn}$.

b) Vẽ tia Ay là tia đối của tia An. Tính $\widehat{mAy}$.

Lời giải:

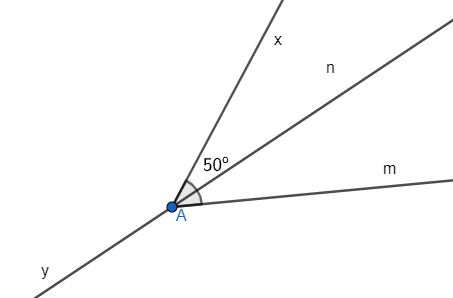
a) Vì An là tia phân giác của góc $\widehat{xAm}$ nên $\widehat{xAn}=\widehat{mAn}=\frac{\widehat{xAM}}{2}=\frac{50°}{2}=25°$.

b) Vì tia Ay là tia đối của tia An nên $\widehat{yAn}=180°$

Do đó, $\widehat{nAm}$ và góc $\widehat{mAy}$ là hai góc kề bù.

Ta có:

$\widehat{nAm}$ + $\widehat{mAy}$ = 180^o

25^o + $\widehat{mAy}$ = 180^o

$\widehat{mAy}$ = 180^o – 25^o

$\widehat{mAy}$ = 155^o.

Vậy $\widehat{mAy}$ = 155^o.

Bài 3.5 trang 37 Tập 1: Cho Hình 3.6. Biết tia Oz là tia phân giác của $\widehat{xOy}$. Tính $\widehat{xOy}$

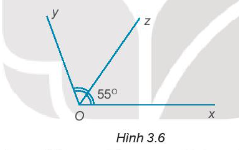
Lời giải:

Vì Oz là tia phân giác của góc $\widehat{xOy}$ nên $\widehat{xOz}=\widehat{zOy}=\frac{\widehat{xOy}}{2}=55°$.

Do đó, $\widehat{xOy}=55°.2=110°$.

Vậy $\widehat{xOy}=110°$.

Bài 3.6 trang 37 Tập 1: Vẽ $\widehat{xAy}=40°$. Vẽ $\widehat{yAz}$ là góc kề bù với $\widehat{xAy}$.

Lời giải:

Bài 3.7 trang 37 Tập 1: Cho góc bẹt xOy. Vẽ tia Oz sao cho $\widehat{xOz}=60°$. Vẽ tia Om là tia phân giác của góc xOz. Vẽ tia On là tia phân giác của góc zOy.

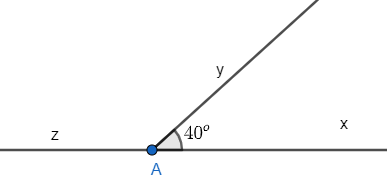
a) Tính số đo góc xOm.

b) Tính số đo góc yOn.

c) Tính số đo góc mOn.

Lời giải:

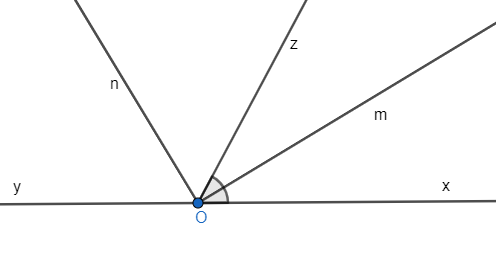
a) Vì Om là tia phân giác của góc $\widehat{xOz}$ nên $\widehat{xOm}=\widehat{mOz}=\frac{\widehat{xOz}}{2}=\frac{60°}{2}=30°$

Vậy $\widehat{xOm}=30°$.

b) Vì góc $\widehat{xOz}$ và $\widehat{yOz}$ là hai góc kề bù nên:

$\widehat{xOz}$ + $\widehat{yOz}$ = 180^o

60^o + $\widehat{yOz}$ = 180⁰

$\widehat{yOz}$ = 180^o – 60⁰

$\widehat{yOz}$ = 120^o

Lại có: On là tia phân giác của góc $\widehat{yOz}$, do đó:

$\widehat{yOn}=\widehat{nOz}=\frac{\widehat{yOz}}{2}=\frac{120°}{2}=60°$

Vậy $\widehat{yOn}=60°$.

c) Ta có: $\widehat{mOn}=\widehat{mOz}+\widehat{zOn}$

$\widehat{mOn}=30°+60°=90°$

Vậy $\widehat{mOn}=90°$.

Bài 3.8 trang 37 Tập 1: Vẽ $\widehat{xOy}=60°$. Vẽ tia Oz là tia đối của tia Ox. Vẽ tia Om là tia phân giác của góc zOy.

a) Tính $\widehat{zOm}$.

b) Vẽ tia On là tia đối của tia Om. Tia Ox có phải là tia phân giác của góc yOn không? Vì sao?

Lời giải:

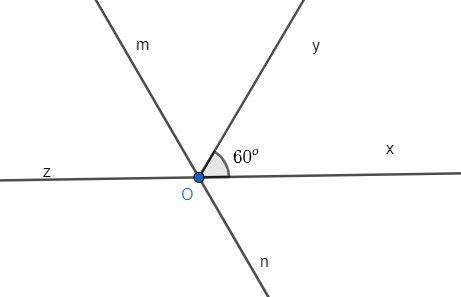
a) Vì Oz và Ox là hai tia đối nhau nên $\widehat{zOx}=180°$. Do đó, $\widehat{zOy}$ và $\widehat{yOx}$ là hai góc kề bù.

$\widehat{zOy}$ + $\widehat{xOy}$ = 180^o

$\widehat{zOy}$ + 60^o = 180^o

$\widehat{zOy}$ = 180^o – 60^o

$\widehat{zOy}$ = 120^o.

Mà Om là tia phân giác của góc $\widehat{zOy}$ nên ta có:

$\widehat{zOm}=\widehat{mOy}=\frac{\widehat{zOy}}{2}$$=\frac{120°}{2}=60°$

Vậy $\widehat{zOm}$ = 60^o.

b) Vì On là tia đối của  tia Om và Oz là tia đối của tia Ox nên $\widehat{mOz};\widehat{nOx}$ đối đỉnh.

Suy ra,

$\widehat{mOz}=\widehat{nOx}$ = 60^o.

Ta có: Ox nằm giữa hai tia Oy và On;

$\widehat{xOy}=\widehat{nOx}$ = 60^o.

Do đó, Ox là tia phân giác của góc $\widehat{yOn}$.

Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 7: Tập hợp các số thực

Ôn tập chương 2

Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết

Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song

Bài 11: Định lí và chứng minh định lí