Giải Sách bài tập Toán lớp 7 Bài 4: Đường vuông góc và đường xiên
Bài 1 trang 52 SBT Toán 7 Tập 2:
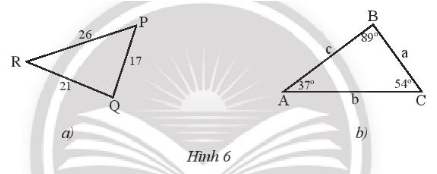
a) Sắp xếp theo thứ tự từ nhỏ đến lớn số đo các góc của tam giác PQR ở Hình 6a.
b) Sắp xếp theo thứ tự từ nhỏ đến lớn độ dài các cạnh của tam giác ABC ở Hình 6b.
Lời giải
a)
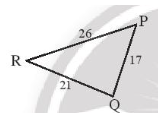
Trong PQR ta có lần lượt đối diện với cạnh QR, cạnh RP, cạnh QP.
Vì PQ < QR < PR (do 17 < 21 < 26) nên theo quan hệ giữa cạnh và góc trong tam giác ta có .
Vậy sắp xếp theo thứ tự từ nhỏ đến lớn số đo các góc của tam giác PQR ta được
b)
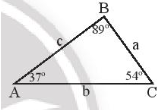
Xét tam giác ABC có (do 37° < 54° < 89°).
Nên BC < AB < AC (quan hệ giữa cạnh và góc trong tam giác)
Hay a < c < b.
Vậy sắp xếp theo thứ tự từ nhỏ đến lớn độ dài các cạnh của tam giác ABC ta được: a, c, b.
Bài 2 trang 52 SBT Toán 7 Tập 2:
Lời giải
a) Vì DEF có góc tù nên là góc lớn nhất.
Do đó cạnh DE đối diện với góc F là cạnh có độ dài lớn nhất (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn).
Vậy DE là cạnh có độ dài lớn nhất trong ba cạnh của tam giác DEF.
b) Vì ABC vuông tại A nên là góc lớn nhất.
Do đó cạnh huyển BC đối diện với góc A là cạnh dài nhất (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn).
Vậy BC là cạnh có độ dài lớn nhất trong ba cạnh của tam giác ABC.
Bài 3 trang 52 SBT Toán 7 Tập 2:
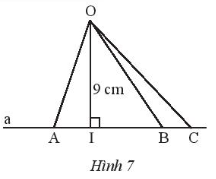
a) tìm đường ngắn nhất trong các đường OA, OI, OB, OC;
b) tìm khoảng cách từ O đến đường thẳng a.
Lời giải
a) Ta có OI là đường vuông góc;
OA, OB, OC là các đường xiên.
Do đó trong các đường OA, OI, OB, OC thì OI là đường ngắn nhất (mối quan hệ giữa đường vuông góc và đường xiên).
Vậy đường OI ngắn nhất.
b) Khoảng cách từ O đến đường thẳng a chính là độ dài đoạn thẳng OI.
Vì OI = 9 cm (giả thiết) nên khoảng cách từ O đến đường thẳng a bằng 9 cm.
Vậy khoảng cách từ O đến đường thẳng a bằng 9 cm.
Bài 4 trang 52 SBT Toán 7 Tập 2:
a) Tìm cạnh lớn nhất của tam giác MNP.
b) Tam giác MNP là tam giác gì? Vì sao?
Lời giải
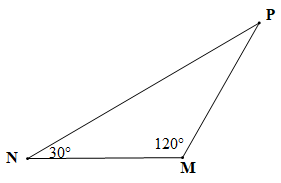
a) Vì MNP có nên là góc tù và là góc lớn nhất trong tam giác MNP.
Do đó cạnh NP đối diện với góc M là cạnh có độ dài lớn nhất (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn).
Vậy NP là cạnh lớn nhất trong ba cạnh của tam giác MNP.
b) Xét MNP có: (định lí tổng ba góc trong một tam giác).
Suy ra
Do đó
Khi đó (cùng bằng 30°).
Suy ra tam giác MNP cân tại M.
Vậy MNP là tam giác cân tại M.
Bài 5 trang 53 SBT Toán 7 Tập 2: Cho tam giác OHK vuông tại O có
a) So sánh các cạnh của tam giác.
b) Lấy điểm M bất kì thuộc đoạn thẳng OH, So sánh độ dài KM và KH.
Lời giải
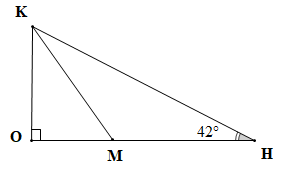
a) Xét ∆OHK vuông tại O ta có: (trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Suy ra .
Xét ∆OHK có (do 90° > 48° > 42°).
Nên KH > OH > OK (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn).
Vậy KH > OH > OK.
b) Ta có và là hai góc kề bù.
Mà trong ∆OKM vuông tại M nên là góc nhọn.
Do đó là góc tù.
Xét KMH có là góc tù nên là góc lớn nhất.
Khi đó cạnh KH đối diện với góc KMH là cạnh có độ dài lớn nhất (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn).
Do đó KH > KM.
Vậy KH > KM.
Lời giải
|
GT |
ABC vuông tại A, BD là tia phân giác của góc ABC (D ∈ AC). |
|
KL |
So sánh AD, CD. |
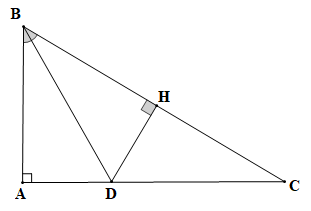
Vẽ DH vuông góc với BC.
• Xét ABD và HBD có:
,
(do BD là tia phân giác của ),
BD là cạnh chung,
Do đó ABD = HBD (cạnh huyền – góc nhọn).
Suy ra AD = HD (hai cạnh tương ứng).
• Vì DHC vuông tại H nên là góc lớn nhất.
Do đó cạnh huyển DC đối diện với góc H là cạnh lớn nhất (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn).
Suy ra DC > DH.
Lại có DH = AD (chứng minh trên).
Nên DC > AD.
Vậy DC > AD.
Xem thêm lời giải sách bài tập Toán lớp 7 bộ sách Chân trời sáng tạo hay, chi tiết nhất:
Bài 5: Đường trung trực của một đoạn thẳng