Giải SBT Toán 7 (Chân trời sáng tạo) Bài 3: Phép cộng và phép trừ đa thức một biến

Giải Sách bài tập Toán lớp 7 Bài 3: Phép cộng và phép trừ đa thức một biến

Giải SBT Toán 7 trang 30 Tập 2

Bài 1 trang 30 SBT Toán 7 Tập 2:

Cho hai đa thức: P(x) = –4x⁴ – 3x² + 7 và Q(x) = 2x⁴ – 5x² + 8x – 1. Hãy tính P(x) + Q(x) và P(x) – Q(x).

Lời giải:

Ta có:

• P(x) + Q(x)

= (–4x⁴ – 3x² + 7) + (2x⁴ – 5x² + 8x – 1)

= –4x⁴ – 3x² + 7 + 2x⁴ – 5x² + 8x – 1

= (–4x⁴ + 2x⁴) + (– 3x² – 5x²) + 8x + (7 – 1)

= –2x⁴ – 8x² + 8x + 6.

• P(x) – Q(x)

= (–4x⁴ – 3x² + 7) – (2x⁴ – 5x² + 8x – 1)

= –4x⁴ – 3x² + 7 – 2x⁴ + 5x² – 8x + 1

= (–4x⁴ – 2x⁴) + (– 3x² + 5x²) – 8x + (7 + 1)

= –6x⁴ + 2x² – 8x + 8.

Vậy P(x) + Q(x) = –2x⁴ – 8x² + 8x + 6 và P(x) – Q(x) = –6x⁴ + 2x² – 8x + 8.

Bài 2 trang 30 SBT Toán 7 Tập 2:

Cho đa thức A(t) = 2t⁴ – 8t³ + 9t + 3.

Tìm đa thức B(t) sao cho B(t) – A(t) = –4t³ + 3t² + 8t.

Lời giải:

Ta có B(t) – A(t) = –4t³ + 3t² + 8t

Suy ra B(t) = A(t) + (–4t³ + 3t² + 8t)

Do đó B(t) = (2t⁴ – 8t³ + 9t + 3) + (–4t³ + 3t² + 8t)

                  = 2t⁴ – 8t³ + 9t + 3 – 4t³ + 3t² + 8t

                  = 2t⁴ + (– 8t³ – 4t³) + 3t² + (9t + 8t) + 3

                  = 2t⁴ – 12t³ + 3t² + 17t + 3

Vậy B(t) = 2t⁴ – 12t³ + 3t² + 17t + 3.

Bài 3 trang 30 SBT Toán 7 Tập 2:

Cho đa thức M(x) = 4x³ – 7x² + 2x – 9.

Tìm đa thức N(x) sao cho M(x) + N(x) = 2x³ – 6x.

Lời giải:

Ta có M(x) + N(x) = 2x³ – 6x

Suy ra N(x) = 2x³ – 6x – M(x)  

Do đó N(x) = 2x³ – 6x – (4x³ – 7x² + 2x – 9)

                   = 2x³ – 6x – 4x³ + 7x² – 2x + 9

                   = (2x³ – 4x³) + 7x² + (– 6x – 2x) + 9

                   = –2x³ + 7x² – 8x + 9.

Vậy N(x) = –2x³ + 7x² – 8x + 9.

Bài 4 trang 30 SBT Toán 7 Tập 2:

Cho ba đa thức P(x) = 3x⁴ – 2x² + 8x – 10; Q(x) = 4x³ – 6x² + 7x – 1 và R(x) = –3x⁴ + 5x² – 8x – 5. Tính P(x) + Q(x) + R(x) và P(x) – Q(x) – R(x).

Lời giải:

Ta có:

• P(x) + Q(x) + R(x)

= (3x⁴ – 2x² + 8x – 10) + (4x³ – 6x² + 7x – 1) + (–3x⁴ + 5x² – 8x – 5)

= 3x⁴ – 2x² + 8x – 10 + 4x³ – 6x² + 7x – 1 – 3x⁴ + 5x² – 8x – 5

= (3x⁴ – 3x⁴) + 4x³ + (– 2x² – 6x² + 5x²) + (8x + 7x – 8x) + (– 10 – 1 – 5)

= 4x³ – 3x² + 7x – 16.

• P(x) – Q(x) – R(x)

= (3x⁴ – 2x² + 8x – 10) – (4x³ – 6x² + 7x – 1) – (–3x⁴ + 5x² – 8x – 5)

= 3x⁴ – 2x² + 8x – 10 – 4x³ + 6x² – 7x + 1 + 3x⁴ – 5x² + 8x + 5

= (3x⁴ + 3x⁴) – 4x³ + (– 2x² + 6x² – 5x²) + (8x – 7x + 8x) + (– 10 + 1 + 5)

= 6x⁴ – 4x³ – x² + 9x – 4.

Vậy P(x) + Q(x) + R(x) = 4x³ – 3x² + 7x – 16;

P(x) – Q(x) – R(x) = 6x⁴ – 4x³ – x² + 9x – 4.

Bài 5 trang 30 SBT Toán 7 Tập 2:

Cho đa thức P(x) = –3x² + 7x – 5. Hãy viết P(x) thành tổng của hai đa thức bậc bốn.

Lời giải:

Ta có:

P(x) = –3x² + 7x – 5

        = –3x² + 7x – 5 + x⁴ – x⁴

        = (x⁴ – 3x²) + (– x⁴ + 7x – 5)

        = M(x)  + N(x)

Vậy với M(x) = x⁴ – 3x² và N(x) = – x⁴ + 7x – 5 thì P(x) được viết thành tổng của hai đa thức bậc bốn.

Nhận xét: Bài này có nhiều cách trả lời.

Bài 6 trang 30 SBT Toán 7 Tập 2:

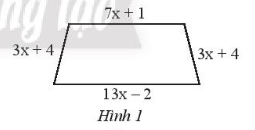
Viết biểu thức biểu thị chu vi của hình thang cân trong Hình 1.

Lời giải:

Chu vi hình thang cân trong Hình 1 là:

(7x + 1) + (3x + 4) + (13x – 2) + (3x + 4)

= 7x + 1 + 3x + 4 + 13x – 2 + 3x + 4

= (7x + 3x + 13x + 3x) + (1 + 4 – 2 + 4)

= 26x + 7.

Vậy chu vi của hình thang cân trong Hình 1 là 26x + 7.

Bài 7 trang 30 SBT Toán 7 Tập 2:

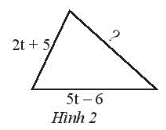
Cho tam giác (xem Hình 2) có chu vi bằng 12t – 6. Hãy tìm cạnh chưa biết của tam giác đó.

Lời giải:

Gọi biểu thức biểu thị độ dài cạnh chưa biết của tam giác trong Hình 2 là A(t).

Khi đó chu vi của tam giác trong Hình 2 là:

(2t + 5) + (5t – 6) + A(t)

= (2t + 5t) + (5 – 6) + A(t)

= 7t – 1 + A(t).

Mà theo bài tam giác có chu vi bằng 12t – 6 nên ta có:

7t – 1 + A(t) = 12t – 6.

Suy ra A(t) = 12t – 6 – (7t – 1)

                    = 12t – 6 – 7t + 1

                    = (12t – 7t) + (– 6 + 1)

                    = 5t – 5.

Vậy độ dài cạnh cần tìm là A(t) = 5t – 5.

Bài 8 trang 30 SBT Toán 7 Tập 2:

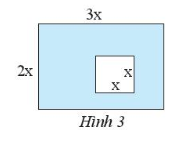
Hãy viết biểu thức biểu thị diện tích của phần được tô đậm trong Hình 3.

Lời giải:

Diện tích của hình chữ nhật có độ dài cạnh 2x và 3x là:

2x . 3x = 6x² (đơn vị diện tích).

Diện tích của hình vuông cạnh x là: x² (đơn vị diện tích).

Diện tích của phần được tô đậm trong Hình 3 là:

6x² – x² = 5x² (đơn vị diện tích).

Vậy biểu thức biểu thị diện tích của phần được tô đậm trong Hình 3 là 5x².

Giải SBT Toán 7 trang 31 Tập 2

Bài 9 trang 31 SBT Toán 7 Tập 2:

Số lượng xe du lịch được bán ra tại một nước từ năm 1983 tới năm 1996 được mô tả theo công thức C = –0,016t⁴ + 0,49t³ – 4,8t² + 14t + 70 (tính bằng đơn vị nghìn chiếc), trong khi đó số xe tải thì tính theo T =  –0,01t⁴ + 0,31t³ – 3t² + 11t + 23, với t là số năm tính từ 1983. Viết biểu thức biểu thị số xe (cả xe du lịch và xe tải) được bán ra trong khoảng thời gian nêu trên. Tính số xe được bán ra vào năm 1990 (ứng với t = 7).

Lời giải:

Tổng số xe được bán ra biểu thị bởi:

C + T

= (–0,016t⁴ + 0,49t³ – 4,8t² + 14t + 70) + (–0,01t⁴ + 0,31t³ – 3t² + 11t + 23)

= –0,016t⁴ + 0,49t³ – 4,8t² + 14t + 70 – 0,01t⁴ + 0,31t³ – 3t² + 11t + 23

= (–0,016t⁴ – 0,01t⁴) + (0,49t³ + 0,31t³) + (–4,8t² – 3t²) + (14t + 11t) + (70 + 23)

= – 0,026t⁴ + 0,8t³ – 7,8t² + 25t + 93

Khi t = 7 thay vào biểu thức C + T ở trên ta có:

C + T = – 0,026 . 7⁴ + 0,8 . 7³ – 7,8 . 7² + 25 . 7 + 93

          = –0,026 . 2 401 + 0,8 . 343 – 7,8 . 49 + 175 + 93

          = –62,426 + 274,4 – 382,2 + 175 + 93

          = 97,774 (nghìn chiếc) = 97 774 chiếc.

Vậy số xe bán ra vào năm 1990 là 97 774 chiếc.

Bài 10 trang 31 SBT Toán 7 Tập 2:

Dân số nước Mỹ từ năm 1980 tới 1996 được tính theo công thức:

P = –0,8t⁴ + 27t³ – 262t² + 3 010t + 227 000.

Và số người từ 85 tuổi trở lên thì tính theo công thức:

S = 0,02t⁴ – 0,7t³ + 6,4t² + 213t + 7 740.

Trong đó P, S tính theo đơn vị nghìn người, t là số năm tính từ 1980.

Viết biểu thức biểu thị số người Mỹ dưới 85 tuổi và tính số người đó vào năm 1995 (ứng với t = 15).

Lời giải:

Số người Mỹ dưới 85 tuổi được biểu thị bởi:

P – S

= (–0,8t⁴ + 27t³ – 262t² + 3 010t + 227 000) – (0,02t⁴ – 0,7t³ + 6,4t² + 213t + 7 740)

= –0,8t⁴ + 27t³ – 262t² + 3 010t + 227 000 – 0,02t⁴ + 0,7t³ – 6,4t² – 213t – 7 740

= (–0,8t⁴ – 0,02t⁴) + (27t³ + 0,7t³) + (– 262t² – 6,4t²) + (3 010t – 213t) + (227 000 – 7 740)

= –0,82t⁴ + 27,7t³ – 268,4t² + 2 797t + 219 260.

Khi t = 15 ta có:

P – S = –0,82 . 15⁴ + 27,7 . 15³ – 268,4 . 15² + 2 797 . 15 + 219 260. 

         = –0,82 . 50 625 + 27,7 . 3 375 – 268,4 . 225 + 41 955 + 219 260. 

         = –41 512,5 + 93 487,5 – 60 390 + 41 955 + 219 260. 

         = 252 800 (nghìn người) = 252 800 000 (người).

Vậy vào năm 1995, số người Mỹ dưới 85 tuổi là vào khoảng 252 800 000 người.

Xem thêm lời giải sách bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

Bài 1: Biểu thức số, biểu thức đại số

Bài 2: Đa thức một biến

Bài 4: Phép nhân và phép chia đa thức một biến

Bài tập cuối chương 7

Bài 1: Góc và cạnh của một tam giác