Giải SBT Toán 7 (Chân trời sáng tạo) Bài tập cuối chương 7

• Giải Sách bài tập Toán lớp 7 Bài tập cuối chương 7

Giải SBT Toán 7 trang 33 Tập 2

Bài 1 trang 33 SBT Toán 7 Tập 2:

Cho B = xy³ + 4xy – 2x² + 3. Tính giá trị của biểu thức B khi x = –1, y = 2.

Lời giải:

Khi x = –1, y = 2 thay vào biểu thức B ta được:

B = (–1) . 2³ + 4 . (–1) . 2 – 2 . (–1)² + 3

    = –8 – 8 – 2 + 3

    = –15.

Vậy giá trị của biểu thức B khi x = –1, y = 2 là B = –15.

Bài 2 trang 33 SBT Toán 7 Tập 2:

Trong các biểu thức sau, biểu thức nào là đơn thức một biến?

a) 2y;           b) 3x + 5;               c) 12;           d) $\frac{1}{3}$ t².

Lời giải:

Ta có:

+ Biểu thức a) là đơn thức một biến của biến y;

+ Biểu thức b) là đa thức một biến của biến x;

+ Biểu thức c) là đơn thức một biến.

+ Biểu thức d) là đơn thức một biến của biến t.

Vậy trong các biểu thức trên, biểu thức a), c), d) là đơn thức một biến.

Bài 3 trang 33 SBT Toán 7 Tập 2:

Trong các biểu thức sau, biểu thức nào là đa thức một biến?

5 – 2x;         6x² + 8x³ + 3x – 2;            $\frac{2}{x-1}$;          $\frac{1}{4}$ t – 5.

Lời giải:

Ta có:

+ Biểu thức 5 – 2x là đa thức một biến của biến x;

+ Biểu thức 6x² + 8x³ + 3x – 2 là đa thức một biến của biến x;

+ Biểu thức $\frac{2}{x-1}$  không phải là đa thức một biến;

+ Biểu thức $\frac{1}{4}$ t – 5 là đa thức một biến của biến t.

Vậy trong các biểu thức trên, các biểu thức là đa thức một biến là: 5 – 2x; 6x² + 8x³ + 3x – 2; $\frac{1}{4}$ t – 5.

Bài 4 trang 33 SBT Toán 7 Tập 2:

Hãy viết một đa thức một biến bậc bốn có 5 số hạng.

Lời giải:

Đa thức một biến bậc bốn có 5 số hạng là:

A(x) = x⁴ – 2x³ + 3x² – 4x + 5.

Nhận xét: Bài này có nhiều cách trả lời.

Bài 5 trang 33 SBT Toán 7 Tập 2:

Hãy nêu bậc của các đa thức sau:

A = 5x² – 2x⁴ + 7;            B = 17;                  C = 3x – 4x³ + 2x² + 1.

Lời giải:

• Ta có:

A = 5x² – 2x⁴ + 7

    = – 2x⁴ + 5x² + 7

Đa thức A có bậc là 4 (vì số mũ lớn nhất của biến x là 4).

• Đa thức B = 17 có bậc là 0 (vì đa thức chỉ có số, không có biến x nên số mũ lớn nhất của biến là 0).

• Ta có:

C = 3x – 4x³ + 2x² + 1

    = – 4x³ + 2x² + 3x + 1

Đa thức C có bậc là 3 (vì số mũ lớn nhất của biến x là 3).

Bài 6 trang 33 SBT Toán 7 Tập 2:

Cho đa thức P(x) = x³ + 64. Tìm nghiệm của P(x) trong tập hợp {0; 4; –4}. 

Lời giải:

Cách 1: Xét đa thức P(x) = x³ + 64.

• Với x = 0 thay vào P(x) ta có:

P(0) = 0³ + 64 = 64.

Do đó x = 0 không là nghiệm của P(x).

• Với x = 4 thay vào P(x) ta có:

P(4) = 4³ + 64 = 64 + 64 = 128.

Do đó x = 4 không là nghiệm của P(x).

• Với x = –4 thay vào P(x) ta có:

P(–4) = (–4)³ + 64 = –64 + 64 = 0.

Do đó x = –4 là nghiệm của P(x).

Vậy trong các số thuộc tập hợp {0; 4; –4} thì có –4 là nghiệm của P(x).

Cách 2: Xét đa thức P(x) = x³ + 64.

Ta có P(x) = 0

Hay x³ + 64 = 0

Suy ra x³ = –64 = (–4)³

Do đó x = –4.

Vậy trong các số thuộc tập hợp {0; 4; –4} thì số –4 là nghiệm của P(x).

Bài 7 trang 33 SBT Toán 7 Tập 2:

Tam giác có độ dài hai cạnh là 3y + 2; 6y – 4 và chu vi bằng 23y – 5. Tìm cạnh chưa biết trong tam giác đó.

Lời giải:

Gọi A(y) là biểu thức biểu thị độ dài cạnh chưa biết trong tam giác đó.

Khi đó chu vi của tam giác đó là:

(3y + 2) + (6y – 4) + A(y)

= (3y + 6y) + (2 – 4) + A(y)

= 9y – 2 + A(y).

Mà theo bài tam giác đó có chu vi bằng 23y – 5 nên ta có:

9y – 2 + A(y) = 23y – 5

Suy ra A(y) = 23y – 5 – (9y – 2)

                    = 23y – 5 – 9y + 2

                    = (23y – 9y) + (–5 + 2)

                    = 14y – 3.

Vậy độ dài cạnh chưa biết trong tam giác đó là A(y) = 14y – 3.

Giải SBT Toán 7 trang 34 Tập 2

Bài 8 trang 34 SBT Toán 7 Tập 2:

Cho đa thức M(x) = 3x⁵ – 4x³ + 9x + 2. Tìm các đa thức N(x), Q(x) sao cho: N(x) – M(x) = –5x⁴ – 4x³ + 2x² + 8x và Q(x) + M(x) = 3x⁴ – 2x³ + 9x² – 7.

Lời giải:

• Ta có: N(x) – M(x) = –5x⁴ – 4x³ + 2x² + 8x

Suy ra N(x) = –5x⁴ – 4x³ + 2x² + 8x + M(x)

Do đó N(x) = –5x⁴ – 4x³ + 2x² + 8x + (3x⁵ – 4x³ + 9x + 2)

                    = –5x⁴ – 4x³ + 2x² + 8x + 3x⁵ – 4x³ + 9x + 2

                    = 3x⁵ – 5x⁴ + (–4x³ – 4x³) + 2x² + (8x + 9x) + 2

                    = 3x⁵ – 5x⁴ – 8x³ + 2x² + 17x + 2.

• Ta có: Q(x) + M(x) = 3x⁴ – 2x³ + 9x² – 7.

Suy ra Q(x) = 3x⁴ – 2x³ + 9x² – 7 – M(x)

Do đó Q(x) = 3x⁴ – 2x³ + 9x² – 7 – (3x⁵ – 4x³ + 9x + 2)

                    = 3x⁴ – 2x³ + 9x² – 7 – 3x⁵ + 4x³ – 9x – 2

                    = – 3x⁵ + 3x⁴ + (– 2x³ + 4x³) + 9x² – 9x + (– 7 – 2)

                    = – 3x⁵ + 3x⁴ + 2x³ + 9x² – 9x – 9.

Vậy N(x) = 3x⁵ – 5x⁴ – 8x³ + 2x² + 17x + 2;

Q(x) = – 3x⁵ + 3x⁴ + 2x³ + 9x² – 9x – 9.

Bài 9 trang 34 SBT Toán 7 Tập 2:

Thực hiện phép nhân.

a) (4x – 5)(3x + 4);

b) (2x² – 3x + 5)(4x + 3).

Lời giải:

a) (4x – 5)(3x + 4)

= 4x(3x + 4) – 5(3x + 4)

= 12x² + 16x – 15x – 20

= 12x² + (16x – 15x) – 20

= 12x² + x – 20.

Vậy (4x – 5)(3x + 4) = 12x² + x – 20.

b) (2x² – 3x + 5)(4x + 3)

= 2x²(4x + 3) – 3x(4x + 3) + 5(4x + 3)

= 8x³ + 6x² – 12x² – 9x + 20x + 15

= 8x³ + (6x² – 12x²) + (– 9x + 20x) + 15

= 8x³ – 6x² + 11x + 15.

Vậy (2x² – 3x + 5)(4x + 3) = 8x³ – 6x² + 11x + 15.

Bài 10 trang 34 SBT Toán 7 Tập 2:

Thực hiện phép chia.

a) (64y² – 16y⁴ + 8y⁵) : 4y;

b) (5t² – 8t + 3) : (t – 1).

Lời giải:

a) (64y² – 16y⁴ + 8y⁵) : 4y;

= (64y² : 4y) + (–16y⁴ : 4y) + (8y⁵ : 4y)

= 16y – 4y³ + 2y⁴.

Vậy (64y² – 16y⁴ + 8y⁵) : 4y = 16y – 4y³ + 2y⁴.

b) (5t² – 8t + 3) : (t – 1)

Thực hiện đặt tính phép chia đa thức như sau:

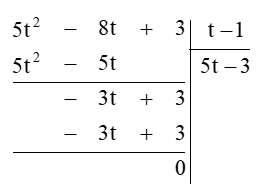
Vậy (5t² – 8t + 3) : (t – 1) = 5t – 3.

Bài 11 trang 34 SBT Toán 7 Tập 2:

Thực hiện phép chia.

a) (x⁴ + 6x² + 8) : (x² + 2);

b) (3x³ – 2x² + 3x – 2) : (x² + 1).

Lời giải:

a) (x⁴ + 6x² + 8) : (x² + 2)

Thực hiện đặt tính phép chia đa thức như sau:

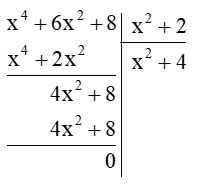
Vậy (x⁴ + 6x² + 8) : (x² + 2) = x² + 4.

b) (3x³ – 2x² + 3x – 2) : (x² + 1)

Thực hiện đặt tính phép chia đa thức như sau:

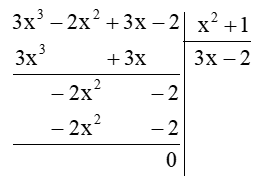
Vậy (3x³ – 2x² + 3x – 2) : (x² + 1) = 3x – 2.

Bài 12 trang 34 SBT Toán 7 Tập 2:

Thực hiện phép chia.

a) (2x² – 7x + 4) : (x – 2);

b) (2x³ + 3x² + 3x + 4) : (x² + 2).

Lời giải:

a) (2x² – 7x + 4) : (x – 2)

Thực hiện đặt tính phép chia đa thức như sau:

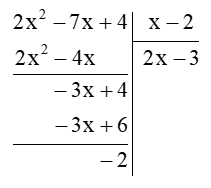
Vậy $\frac{2x^2-7x+4}{x-2}=2x-3-\frac{2}{x-2}.$

b) (2x³ + 3x² + 3x + 4) : (x² + 2).

Thực hiện đặt tính phép chia đa thức như sau:

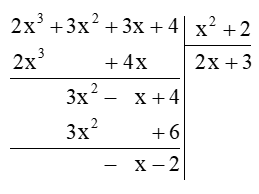
Vậy  $\frac{2x^3+3x^2+3x+4}{x^2+2}=2x+3-\frac{x+2}{x^2+2}.$

Xem thêm lời giải sách bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

Bài 3: Phép cộng và phép trừ đa thức một biến

Bài 4: Phép nhân và phép chia đa thức một biến

Bài 1: Góc và cạnh của một tam giác

Bài 2: Tam giác bằng nhau

Bài 3: Tam giác cân