Sách bài tập Toán 6 Bài 13: Bội chung. Bội chung nhỏ nhất
Bài 1 trang 32 sách bài tập Toán lớp 6 Tập 1: Tìm
a) BC(6,10);
b) BC(9,12).
Lời giải:
a) Ta có:
B(6) = {0; 6; 12; 18; 24; 30; 36; 42; 48; 54; 60;…}
B(10) = {0; 20; 30; 40; 50; 60; …}
⇒ BC(6,10) = {0; 30; 60; …}.
Vậy BC(6,10) = {0; 30; 60; …}.
b) Ta có:
B(9) = {0; 9; 18; 27; 36; 45; 54; 63; 72;…}
B(12) = {0; 24; 36; 48; 60; 72; …}
⇒ BC(9,12) = {0; 36; 72; …}.
Vậy BC(9,12) = {0; 36; 72; …}.
Bài 2 trang 32 sách bài tập Toán lớp 6 Tập 1: Tìm BCNN của:
a) 1 và 8
b) 8; 1 và 12
c) 36 và 72
d) 5 và 24
Lời giải:
a) Vì 8 chia hết cho 1 nên BCNN(1,8) = 8.
b) Vì 8 và 12 đều chia hết cho 1 nên BCNN(8,1,12) = BCNN(8,12).
Ta có 8 = 23, 12 = 22.3
Lập tích các thừa số chung và riêng mỗi thừa số lấy số mũ lớn nhất là: 23.3 = 24.
Suy ra BCNN(8,12) = 23.3 = 8.3 = 24.
Vậy BCNN(8,1,12) = 24.
c) Vì 72 = 36.2 nên 72 chia hết cho 36. Do đó BCNN(36,72) = 72.
d) Ta có 5 = 5 và 24 = 23.3
Lập tích các thừa số chung và riêng mỗi thừa số lấy số mũ lớn nhất là: 23.3.5.
Suy ra BCNN(5,24) = 23.3.5 = 120.
Vậy BCNN(5,24) = 120.
Bài 3 trang 32 sách bài tập Toán lớp 6 Tập 1: Tìm BCNN của:
a) 17 và 27
b) 45 và 48
c) 60 và 150
d) 10, 12 và 15
Lời giải:
a) Ta có: 17 = 17 và 27 = 33
Lập tích các thừa số chung và riêng mỗi thừa số có số mũ nhỏ nhất là: 33.17
Suy ra BCNN(17, 27) = 33.17 = 459.
Vậy BCNN(17, 27) = 459.
b) Ta có: 45 = 32.5 và 48 = 24.3
Lập tích các thừa số chung và riêng mỗi thừa số có số mũ nhỏ nhất là: 24.32.5.
Suy ra BCNN(45, 48) = 24.32.5 = 720.
Vậy BCNN(45,48) = 720.
c) Ta có: 60 = 22.3.5 và 150 = 2.3.52
Lập tích các thừa số chung và riêng mỗi thừa số có số mũ nhỏ nhất là: 22.3.52.
Suy ra BCNN(60, 150) = 22.3.52 = 300.
Vậy BCNN(60,15) = 300.
d) Ta có: 10 = 2.5, 12 = 22.3, 15 = 3.5
Lập tích các thừa số chung và riêng mỗi thừa số có số mũ nhỏ nhất là: 22.3.5.
Suy ra BCNN(10, 12, 15) = 22.3.5 = 60.
Vậy BCNN(10,12,15) = 60.
a) 30 và 150
b) 40; 28 và 140
c) 100; 120 và 200
Lời giải:
a) Ta có: 150 = 30.5 nên 150 chia hết cho 30
⇒ BCNN(30,150) = 150.
Vậy BCNN(30,150) = 150.
b) Ta lấy 140 nhân lần lượt với 1; 2; 3, … ta thấy: 140.2 = 280 chia hết cho 40 và 140
⇒ BCNN(28,40,140) = 280.
Vậy BCNN(28,40,140) = 280.
c) Ta lấy 200 nhân lần lượt với 1; 2; 3, … ta thấy: 200.3 = 600 chia hết cho 100 và 120
⇒ BCNN(100,120,200) = 600.
Vậy BCNN(100,120,200) = 600.
Bài 5 trang 32 sách bài tập Toán lớp 6 Tập 1: Tìm các bội chung nhỏ hơn 500 của 30 và 45.
Lời giải:
Ta có: 30 = 2.3.5, 45 = 32.5
Suy ra BCNN(30,45) = 2.32.5 = 90.
Suy ra BC(30,45) = B(90) = {0; 60; 180; 270; 360; 450; 540; …}
Tập các bội chung nhỏ hơn 500 của 30 và 45 là: {0; 90; 180; 270; 360; 450}.
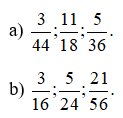
Lời giải:
a) Ta có: 44 = 22.11; 18 = 2.32, 36 = 22.32.
Suy ra BCNN(44, 18, 36) = 22.32.11 = 396.
Khi đó, ta có:
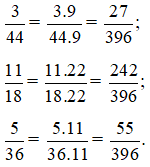
b) Cách 1: Ta có: 16 = 24, 24 = 23.3, 56 = 23.7
Suy ra BCNN(16,24,56) = 24.3.7 = 336.
Khi đó, ta có:
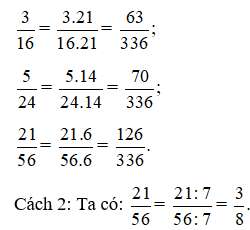
16 = 24, 24 = 23.3, 8 = 23
Suy ra BCNN(16,24,56) = 24.3 = 48.
Khi đó, ta có:
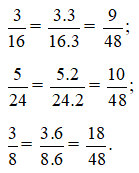
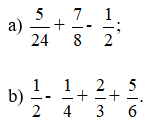
Lời giải:

Lời giải:
Vì xếp hàng 12, hàng 15, hàng 18 đều vừa đủ nên số học sinh này chia hết cho cả 12, 15 và 18.
Do đó số học sinh khối 6 là bội chung của 12, 15 và 18.
Ta có: 12 = 22.3, 15 = 3.5, 18 = 2.32
Suy ra BCNN(12, 15, 18) = 22.32.5 = 180
Nên BC(12,15,18) = B(180) = {0; 180; 360; 540; …}.
Mà số học sinh khối 6 nằm trong khoảng 300 đến 400 học sinh nên số học sinh khối 6 của trường Kết Đoàn là 360 học sinh.
Vậy số học sinh khối 6 của trường Kết Đoàn là 360 học sinh.
Xem thêm các bài giải SBT Toán 6 Chân trời sáng tạo hay, chi tiết khác:
Bài 10. Số nguyên tố. Hợp số. Phân tích một số ra thừa một số nguyên tố
Bài 12. Ước chung. Ước chung lớn nhất
Bài 2. Thứ tự trong tập hợp số nguyên

