Sách bài tập Toán 6 Bài 10: Số nguyên tố. Hợp số. Phân tích một số ra thừa một số nguyên tố
Bài 1 trang 28 sách bài tập Toán lớp 6 Tập 1: Gọi P là tập hợp các số nguyên tố.
Điền kí hiệu ∈, ∉ thích hợp vào chỗ chấm.
41 … P;
57 … P;
83 … P;
95 … P.
Lời giải:
41 chỉ có hai ước là 1 và chính nó nên 41 là số nguyên tố. Suy ra 41∈P.
57 có tổng các chữ số là: 5 + 7 = 12 chia hết cho 3 nên 57 chia hết 3, nghĩa là 57 có nhiều hai ước nên 57 là hợp số. Suy ra 57∉ P.
83 chỉ có hai ước là 1 và chính nó nên 83 là số nguyên tố. Suy ra 83∈ P.
95 có chữ số tận cùng là 5 nên 95 chia hết cho 5, nghĩa là 95 có nhiều hơn hai ước nên 95 là hợp số. Suy ra 95∉ P.
117; 131; 313; 469; 647.
Lời giải:
Quan sát vào bảng nguyên tố, ta thấy các số nguyên tố là: 131; 313; 647.
Bài 3 trang 28 sách bài tập Toán lớp 6 Tập 1: Thay chữ số thích hợp vào dấu * để được mỗi số sau là:
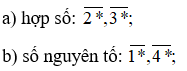
Lời giải:

|
Kết luận |
Đáp số |
|
i. Mỗi số chẵn lớn hơn 2 đều là hợp số. |
|
|
ii. Tổng của hai số nguyên tố lớn hơn 2 luôn là một hợp số |
|
|
iii. Tổng của hai hợp số luôn là một hợp số. |
|
|
iv. Tích của hai số nguyên tố có thể là một số chẵn |
|
b) Với mỗi kết luận sai trong câu a, hãy cho ví dụ minh hoạ.
Lời giải:
a) - Tất cả mọi số chẵn lớn hơn 2 đều là hợp số. Do đó i) đúng.
- Mọi số nguyên tố lớn hơn 2 đều là các số lẻ. Mà tổng hai số lẻ này là một số chẵn lớn hơn 2 nên tổng hai số nguyên tố lớn hơn 2 này chia hết cho 2. Do đó chúng có nhiều hơn hai ước và là một hợp số. Suy ra ii) là đúng.
- Hai hợp số là 25 và 12 có tổng là 25 + 12 = 37 là một số nguyên tố. Do đó iii) là sai.
- Vì có một số nguyên tố chẵn duy nhất là 2 nên tích của số 2 với bất kì số nguyên tố nào khác đều là số chẵn. Chẳng hạn như tích của 2 và của 17 là 2.17 = 34 là một số chẵn. Do đó iv) đúng.
Ta có bảng sau:
|
Kết luận |
Đáp số |
|
i. Mỗi số chẵn lớn hơn 2 đều là hợp số. |
Đ |
|
ii. Tổng của hai số nguyên tố lớn hơn 2 luôn là một hợp số |
Đ |
|
iii. Tổng của hai hợp số luôn là một hợp số. |
S |
|
iv. Tích của hai số nguyên tố có thể là một số chẵn |
Đ |
b) Ví dụ minh họa:
Hai hợp số là 25 và 12 có tổng là 25 + 12 = 37 là một số nguyên tố. Do đó iii) là sai.
b) Viết 15 thành tổng của 3 số nguyên tố.
Lời giải:
a) Ta có: 16 = 5 + 11 = 3 + 13;
18 = 5 + 13 = 7 + 11 ;
20 = 3 + 17 = 7 + 13
b) Ta có: 15 = 3 + 5 + 7
a) 154;
b) 187;
c) 630.
Lời giải:
a) Cách 1: Phân tích một số ra thừa số nguyên tố theo cột dọc:
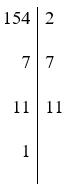
Vậy 154 = 2.7.11.
Cách 2: Phân tích một số ra thừa số nguyên tố bằng sơ đồ cây:
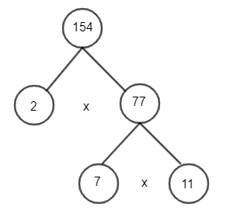
Vậy 154 = 2.7.11.
b) Cách 1: Phân tích một số ra thừa số nguyên tố theo cột dọc:
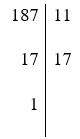
Vậy 187 = 11.17
Cách 2: Phân tích một số ra thừa số nguyên tố bằng sơ đồ cây:
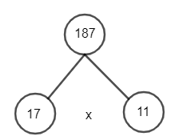
Vậy 187 = 11.17.
c) Cách 1: Phân tích một số ra thừa số nguyên tố theo cột dọc:
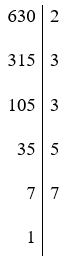
Vậy 630 = 2.32.5.7.
Cách 2: Phân tích một số ra thừa số nguyên tố bằng sơ đồ cây:
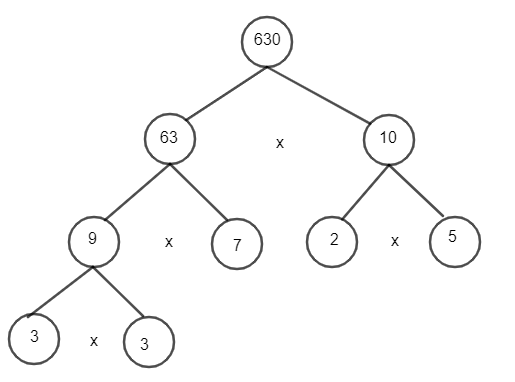
Vậy 630 = 2.32.5.7.
a) 38;
b) 75;
c) 100.
Lời giải:
a) 38 = 2.19
Tập hợp các ước của 38 là: {1; 2; 19; 38}.
b) Ta có: 75 = 3.52
Tập hợp các ước của 75 là: {1; 3; 5; 15; 25; 75}.
c) 100 = 2.2.5.5 = 22.52.
Tập hợp các ước của 100 là: {1; 2; 4; 5; 10; 20; 25; 50; 100}.

Lời giải:
Nếu đựng trứng bằng khay Hình 1:
Quan sát Hình 1, dễ thấy: Khay có 3 hàng, mỗi hàng có 6 quả trứng.
Do đó mỗi khay ở Hình 1 đựng được số trứng là: 3.6 = 18 (quả)
Cần số khay để đựng 360 quả trứng là: 360 : 18 = 20 (khay).
Nếu đựng trứng bằng khay Hình 2:
Quan sát hình 2, dễ thấy: Khay có 5 hàng, mỗi hàng có 6 quả trứng.
Do đó mỗi khay ở Hình 2 đựng được số trứng là: 5.6 = 30 (quả)
Cần số khay để đựng 360 quả trứng là: 360 : 30 = 12 (khay).
Vậy nếu đựng trứng bằng khay Hình 1 thì cần dùng 20 khay, nếu đựng trứng bằng khay Hình 2 thì cần dùng 12 khay.
Lời giải:
Trường hợp 1: p chẵn
Do p là số nguyên tố nên p = 2, suy ra p + 1 = 3 và p + 5 = 7 đều là các số nguyên tố.
Vậy p = 2 thỏa mãn.
Trường hợp 2: p lẻ, do p là số nguyên tố nên p > 2
Khi đó p + 1 và p + 5 đều là các số chẵn lớn hơn 2, vì vậy p + 1 và p + 5 là hợp số.
Vậy với p = 2 thì p + 1 và p + 5 đều là số nguyên tố.
Bài 10 trang 29 sách bài tập Toán lớp 6 Tập 1: a) Tìm số tự nhiên k để 3.k là số nguyên tố.
b) Tìm số tự nhiên k để 7.k là số nguyên tố.
Lời giải:
a)
Nếu k = 0 thì 3k = 0, không là số nguyên tố
Nếu k = 1 thì 3k = 3 là một số nguyên tố
Nếu k >1, ta có 3.k chia hết cho 3 và k, do đó nó có ít nhất 3 ước là 1; 3; 3.k nên không là số nguyên tố.
Vậy k = 1 thì 3k là số nguyên tố.
b)
Nếu k = 0 thì 7k = 0, không là số nguyên tố
Nếu k = 1 thì 7k = 7 là một số nguyên tố
Nếu k > 1, ta có 7.k chia hết cho 7 và k, do đó nó có ít nhất 3 ước là 1; 7; 7.k nên không là số nguyên tố.
Vậy k = 1 thì 7k là số nguyên tố.
Xem thêm các bài giải SBT Toán 6 Chân trời sáng tạo hay, chi tiết khác:
Bài 8. Dấu hiệu chia hết cho 3 và cho 9
Bài 12. Ước chung. Ước chung lớn nhất

