Định lý Talet trong hình thang
1. Phương pháp giải
Nếu một đường thẳng song song với hai đáy của hình thang và cắt hai cạnh bên thì nó định ra trên hai cạnh bên đó những đoạn thẳng tương ứng tỉ lệ.
Cho hình thang ABCD, điểm E thuộc AD và F thuộc BC
Nếu EF // AB // CD, ta có AEDE=BFCF
Ngược lại, nếu: AEDE=BFCF => EF // AB// CD
2. Ví dụ minh họa
Ví dụ:
Cho hình vẽ sau:
.png)
trong đó MN song song HG, FN = 12 cm, HM = 18 cm, FG= 36 cm. Độ dài EH bằng bao nhiêu?
Lời giải:
Ta có: MN song song với HG thì các tỷ số như sau:
Thay các số liệu vào:
2 x EH = 18 x 3
2 x EH = 54
EH = 27 (cm)
Đáp số: 27 cm
3. Bài tập vận dụng
Bài 1. Viết tỉ số của các cặp đoạn thẳng có độ dài như sau:
a) AB = 6 cm; CD = 10 cm.
b) AB = 2dm; MN = 4cm.
c) MN = 12 cm; PQ = 2dm
Bài 2: Tìm giá trị của x trên hình vẽ.
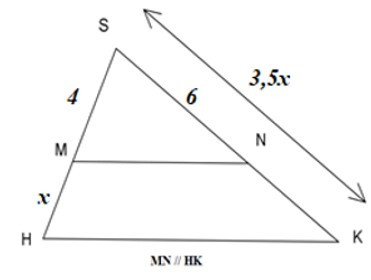
A. x = 3
B. x = 2,5
B. x = 1
D. x = 3,5
Bài 3: Cho hình vẽ, trong đó DE // BC, AE = 12, DB = 18, CA = 36. Độ dài AB bằng:
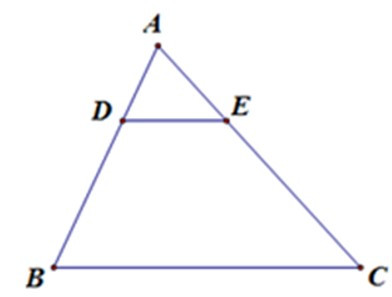
A. 30
B. 36
C. 25
D. 27
Câu hỏi tự luận
Bài tập 1: Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với A qua điểm B trên tia đối của tia HA lấy điểm E sao cho HE = 2HA. Gọi I là hình chiếu của D trên HE. Tính AB, AC, HC biết AH = 4cm, HB = 3cm
Bài tập 2: Cho hình bình hành ABCD. Gọi E, F, G lần lượt là trung điểm của AB,BC,CD. Dùng định lý Talet để chứng minh 2 đoạn thẳng DE và BG chia AC thành 3 đoạn bằng nhau
Bài tập 3: Cho hình thang ABCD có đáy nhỏ CD, từ D kẻ DK // BC (K thuộc AB), DK cắt AC tại M. Vẽ CF // AD (F thuộc AB). Qua F kẻ FP // AC (P thuộc BC). Chứng minh MP // AB
Bài tập 4: Cho tam giac ABC có M là trung điểm của AB, Từ M kẻ đường thẳng song song với BC cắt AC tại N. Chứng minh rằng N là trung điểm của AC
Bài tập 5: Áp dụng định lý Talet. Cho tam giác ABC, các trung tuyến AD, BE, CF cắt nhau tại G. Tính AE/AC
Bài tập 6: Trên cạnh BC của hình vuông ABCD, lấy một đoạn BE = 1/3BC. Trên tia đối của tia CD, lấy một điểm F sao cho CF = 1/2BC, M là giao điểm của AE và BF. Chứng minh AM vuông góc với CM.
Bài 7: Hình thang ABCD (AB//CD, AB
Bài 8: Cho hình thang ABCD (AB//CD, AB
Bài 9: Cho hình thang ABCD (AB//CD, AB
a) MN // AB
b) MN=CD-AB/2
Bài 10: Hình thang ABCD (AB//CD,AB
Bài 11: Cho hình thang ABCD (AB//CD,AB
a) Chứng minh: IK // AB.
b) Đường thẳng IK cắt AD, BC theo thứ tự ở E và F. Chứng minh: EI = IK = KF.
Bài 12: Cho hình thang ABCD có BC // AD. Trên AC kéo dài lấy 1 điểm P tùy ý . Đường thẳng qua P và trung điểm của BC cắt AB tại M và đường thẳng qua P và trung điểm của AD cắt CD tại N. Chứng minh rằng MN // AD.
Xem thêm các dạng bài tập khác:
50 bài tập về hình thang, hình thang vuông, hình thang cân (có đáp án 2024)
50 Bài tập về hình chữ nhật. hình thoi. hình bình hành. hình thang cân (có đáp án năm 2024)
20 bài tập về Hình chữ nhật, Hình thoi, Hình bình hành, Hình thang cân (2024)
50 Bài tập Hình thang. Diện tích hình thang (có đáp án năm 2024)




