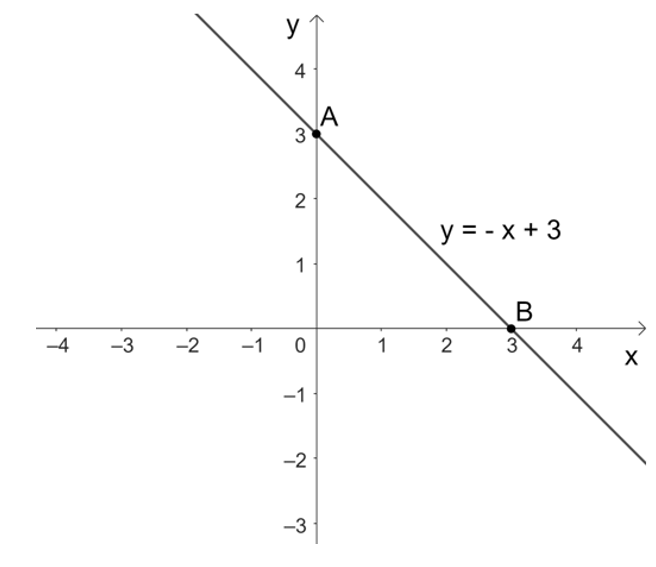Bài 4 trang 77 Toán 8 Tập 1: Xác định đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng – 1 và đi qua điểm M(1; 2). Sau đó vẽ đường thẳng tìm được trên mặt phẳng tọa độ.
Theo đề bài, đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng – 1 nên đường thẳng có dạng y = – x + b.
Mặt khác, đường thẳng đi qua điểm M(1; 2) nên ta có:
– 1 + b = 2 suy ra b = 3.
Do đó, đường thẳng cần tìm là y = – x + 3.
• Với x = 0 thì y = – 0 + 3 = 0 + 3 = 3, ta được điểm A(0; 3) thuộc đồ thị của hàm số y = – x + 3.
• Với y = 0 thì – x + 3 = 0 suy ra x = 3, ta được điểm B(3; 0) thuộc đồ thị của hàm số y = – x + 3.
Do đó, đồ thị của hàm số y = – x + 3 là đường thẳng đi qua hai điểm A(0; 3) và B(3; 0).
Ta vẽ đồ thị hàm số như sau:
Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:
Bài 2: Mặt phẳng tọa độ. Đồ thị của hàm số
Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0)