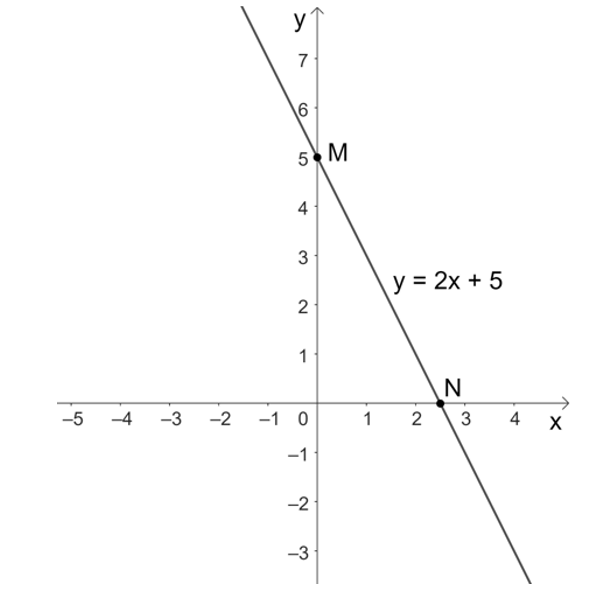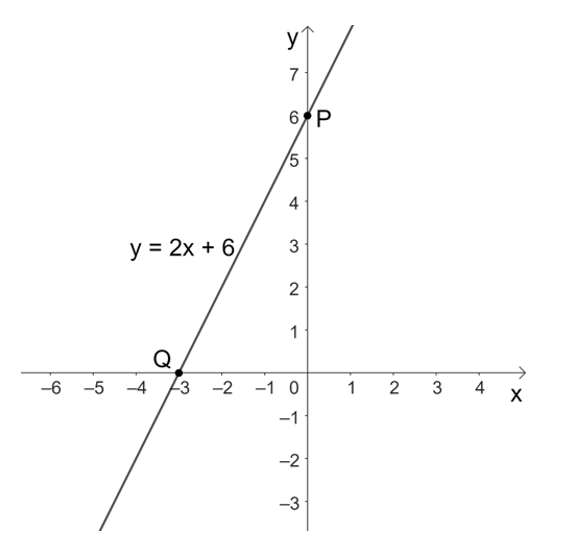Giải SGK Toán 8 (Cánh Diều) Bài tập cuối chương 3

Giải bài tập Toán lớp 8 Bài tập cuối chương 3

Video bài giải Toán lớp 8 Bài tập cuối chương 3 - Cánh diều

Bài 1 trang 78 Toán 8 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai về hai đường thẳng

d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0)?

a) Nếu hai đường thẳng d và d’ song song với nhau thì a = a’, b ≠ b’.

b) Nếu hai đường thẳng d và d’ song song với nhau thì a = a’, b = b’.

c) Nếu hai đường thẳng d và d’ cắt nhau thì a ≠ a’.

d) Nếu hai đường thẳng d và d’ cắt nhau thì a ≠ a’, b ≠ b’.

Lời giải:

Với hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0)

• Nếu hai đường thẳng d và d’ song song với nhau thì a = a’, b ≠ b’.

Do đó, khẳng định a) đúng, khẳng định b) sai.

• Nếu hai đường thẳng d và d’ cắt nhau thì a ≠ a’.

Do đó, khẳng định c) đúng, khẳng định d) sai.

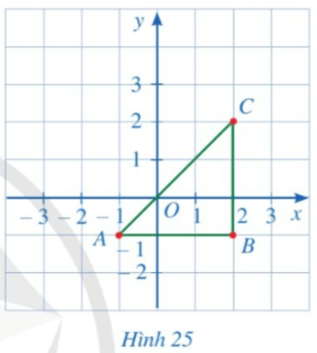
Bài 2 trang 78 Toán 8 Tập 1: Cho tam giác ABC như Hình 25.

a) Xác định tọa độ các điểm A, B, C.

b) Tam giác ABC có là tam giác vuông cân hay không?

c) Gọi D là điểm để tứ giác ABCD là hình vuông. Xác định tọa độ điểm D.

Lời giải:

a) • Hình chiếu của điểm A trên trục hoành là điểm – 1 và trên trục tung là điểm – 1.

Do đó, tọa độ điểm A là A(– 1; – 1).

• Hình chiếu của điểm B trên trục hoành là điểm 2 và trên trục tung là điểm – 1.

Do đó, tọa độ điểm B là B(2; – 1).

• Hình chiếu của điểm C trên trục hoành là điểm 2 và trên trục tung là điểm 2.

Do đó, tọa độ điểm C là C(2; 2).

Vậy tọa độ các điểm A, B, C lần lượt là A(– 1; – 1); B(2; – 1); C(2; 2).

b) Dựa vào các ô vuông trên hình vẽ, ta có AB // Ox; BC // Oy.

Mà Ox ⊥ Oy nên AB ⊥ BC hay $\widehat{B}=90°$.

Ta thấy AB = BC (= 3 ô vuông).

Xét tam giác ABC có $\widehat{B}=90°$ và AB = BC nên tam giác ABC là tam giác vuông cân.

c) Tam giác ABC vuông cân tại A (AB = BC; $\widehat{ABC}=90°$) nên để tứ giác ABCD là hình vuông thì $\widehat{DAB}=90°;\widehat{DCB}=90°$ và AB = BC = CD = DA.

Hay AB ⊥ AD; BC ⊥ CD và AB = BC = CD = DA.

• Qua điểm A, ta kẻ đường thẳng vuông góc với trục Oy.

• Qua điểm C, ta kẻ đường thẳng vuông góc với trục Ox.

 Hai đường thẳng này cắt nhau tại điểm D.

• AD cắt trục Oy tại điểm 1 nên điểm D có tung độ bằng 1.

• CD cắt trục Ox tại điểm 2 nên điểm D có hoành độ bằng 2.

Do đó, tọa điểm D là D(2; 1).

Vậy để tứ giác ABCD là hình vuông thì D(2; 1).

Bài 3 trang 78 Toán 8 Tập 1: Càng lên cao không khí càng loãng nên áp suất khí quyển càng giảm. Chẳng hạn, các khu vực của Thành phố Hồ Chí Minh đều có độ cao sát mực nước biển nên có áp suất khí quyển là p = 760 mmHg; thành phố Puebla (Mexico) có độ cao h = 2 200 m so với mực nước biển nên có áp suất khí quyển là p = 550,4 mmHg. Người ta ước lượng được áp suất khí quyển p (mmHg) tương ứng với độ cao h (m) so với mực nước biển là một hàm số bậc nhất có dạng p = ah + b (a ≠ 0).

a) Xác định hàm số bậc nhất đó.

b) Cao nguyên Lâm Đồng có độ cao 650 m so với mực nước biển thì áp suất khí quyển là bao nhiêu mmHg (làm tròn đến hàng phần mười)?

Lời giải:

a) Các khu vực của Thành phố Hồ Chí Minh đều có độ cao sát mực nước biển nên có áp suất khí quyển là p = 760 mmHg hay ở độ cao h = 0 m thì có áp suất khí quyển là p = 760 mmHg.

Thay h = 0 m; p = 760 mmHg vào hàm số bậc nhất p = ah + b, ta được:

a . 0 + b = 760 hay b = 760.

Do đó hàm số bậc nhất có dạng p = ah + 760.

Mặt khác, thành phố Puebla (Mexico) có độ cao h = 2 200 m so với mực nước biển nên có áp suất khí quyển là p = 550,4 mmHg.

Thay h = 2 200 m; p = 550,4 mmHg vào hàm số bậc nhất p = ah + 760, ta được:

a . 2 200 + 760 = 550,4

2 200a = – 209,6

$a=-\frac{131}{1375}$.

Vậy hàm số bậc nhất cần tìm là $p=-\frac{131}{1375}h+760$.

b) Cao nguyên Lâm Đồng có độ cao 650 m so với mực nước biển thì áp suất khí quyển là

$p=-\frac{131}{1375}.650+760\approx \mathrm{698,1}$ (mmHg).

Vậy cao nguyên Lâm Đồng có độ cao 650 m so với mực nước biển thì áp suất khí quyển khoảng 698,1 mmHg.

Bài 4 trang 78 Toán 8 Tập 1: Cho hai hàm số $y=-\frac{1}{2}x+3;y=2x-2.$

a) Vẽ đồ thị hai hàm số đó trên cùng một mặt phẳng tọa độ.

b) Gọi A, B lần lượt là giao điểm của hai đường thẳng $y=-\frac{1}{2}x+3;y=2x-2.$ với trục hoành và C là giao điểm của hai đường thẳng đó. Tính chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là centimét).

Lời giải:

Cho hai hàm số $y=-\frac{1}{2}x+3;y=2x-2.$

a) * Hàm số $y=-\frac{1}{2}x+3$.

• Với x = 0 thì $y=-\frac{1}{2}.0+3=0+3=3$, ta được điểm M(0; 3) thuộc đồ thị của hàm số $y=-\frac{1}{2}x+3$

• Với y = 0 thì $-\frac{1}{2}x+3=0$ suy ra x = 6, ta được điểm N(6; 0) thuộc đồ thị của hàm số $y=-\frac{1}{2}x+3.$

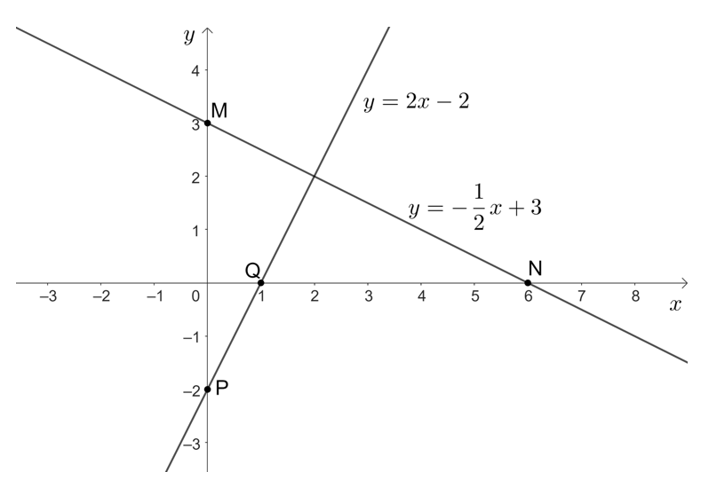
Do đó, đồ thị của hàm số $y=-\frac{1}{2}x+3.$ là đường thẳng đi qua hai điểm M(0; 3) và N(6; 0).

* Hàm số y = 2x – 2.

• Với x = 0 thì y = 2 . 0 – 2 = 0 – 2 = – 2 , ta được điểm P(0; – 2) thuộc đồ thị của hàm số y = 2x – 2.

• Với y = 0 thì 2x – 2 = 0 suy ra x = 1, ta được điểm Q(1; 0) thuộc đồ thị của hàm số y = 2x – 2.

Do đó, đồ thị của hàm số y = 2x – 2 là đường thẳng đi qua hai điểm P(0; – 2) và Q(1; 0).

Ta vẽ đồ thị hai hàm số đó trên cùng một mặt phẳng tọa độ như sau:

b) Gọi A, B lần lượt là giao điểm của hai đường thẳng $y=-\frac{1}{2}x+3;y=2x-2$ với trục hoành và C là giao điểm của hai đường thẳng đó.

Khi đó A ≡ N; B ≡ Q.

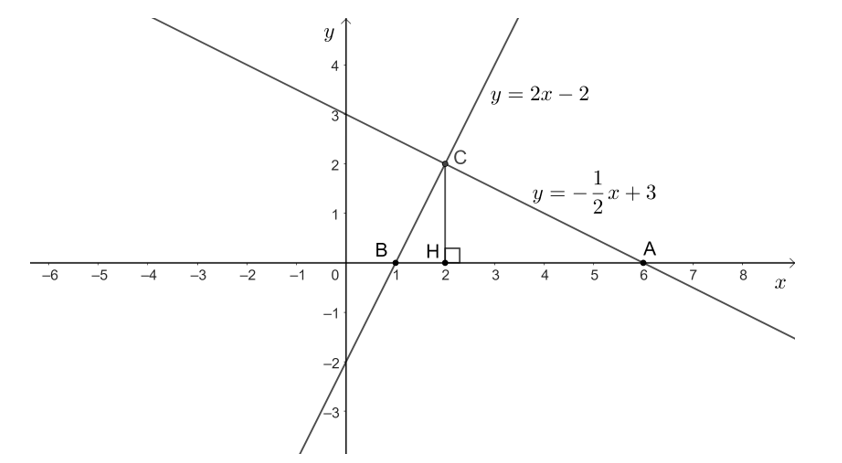
Gọi H là hình chiếu của C trên AB hay CH là đường cao của tam giác ABC.

Ta có đồ thị hàm số như sau:

Dựa vào hình vẽ, ta có:

• Tọa độ điểm C là C(2; 2);

• H là hình chiếu của C trên Ox nên tọa độ điểm H là H(2; 0) suy CH = 2 cm.

• Độ dài AB bằng: 6 – 1 = 5 (cm).

• Độ dài BH bằng: 2 – 1 = 1 (cm).

• Độ dài AH bằng: 6 – 2 = 4 (cm).

Áp dụng định lý Pythagore, ta có:

• AC² = AH² + CH² = 4² + 2² = 20.

Suy ra $AC=\sqrt{20}$ cm.

• BC² = BH² + CH² = 1² + 2² = 5.

Suy ra $BC=\sqrt{5}$ cm.

Khi đó, chu vi tam giác ABC là:

$AB+BC+AC=5+\sqrt{5}+\sqrt{20}\approx \mathrm{11,71}$ (cm)

Diện tích tam giác ABC là:

$\frac{1}{2}AB.CH=\frac{1}{2}.5.2=5$ (cm²).

Vậy chu vi tam giác ABC khoảng 11, 71 cm và diện tích của tam giác ABC bằng 5 cm².

Bài 5 trang 79 Toán 8 Tập 1: a) Biết rằng với x = 3 thì hàm số y = 2x + b có giá trị là 11. Tìm b và vẽ đồ thị của hàm số với giá trị b vừa tìm được.

b) Biết rằng đồ thị của hàm số y = ax + 6 đi qua điểm A(− 2; 2). Tìm a và vẽ đồ thị của hàm số với giá trị a vừa tìm được.

Lời giải:

a) Với x = 3 thì hàm số y = 2x + b có giá trị là 11 tức là

2 . 3 + b = 11

6 + b = 11

b = 11 – 6 = 5.

Khi đó, ta có đồ thị của hàm số y = 2x + 5.

• Với x = 0 thì y = 2 . 0 + 5 = 0 + 5 = 5, ta được điểm M(0; 5) thuộc đồ thị của hàm số y = 2x + 5.

• Với y = 0 thì 2x + 5 = 0 suy ra $x=\frac{-5}{2}$, ta được điểm $N\left(\frac{-5}{2};0\right)$ thuộc đồ thị của hàm số y = 2x + 5.

Do đó, đồ thị của hàm số y = 2x + 5 là đường thẳng đi qua hai điểm M(0; 5) và $N\left(\frac{-5}{2};0\right)$

Ta vẽ đồ thị của hàm số y = 2x + 5 như sau:

b) Đồ thị của hàm số y = ax + 6 đi qua điểm A(− 2; 2) nên – 2a + 6 = 2

Suy ra – 2a = – 4 do đó a = 2.

Khi đó, đồ thị của hàm số cần tìm là y = 2x + 6.

• Với x = 0 thì y = 2 . 0 + 6 = 0 + 6 = 6, ta được điểm P(0; 6) thuộc đồ thị của hàm số y = – 2x + 6.

• Với y = 0 thì 2x + 6 = 0 suy ra x = – 3, ta được điểm Q(– 3; 0) thuộc đồ thị của hàm số y = – 2x + 6.

Do đó, đồ thị của hàm số y = 2x + 6 là đường thẳng đi qua hai điểm P(0; 6) và Q(– 3; 0).

Ta vẽ đồ thị của hàm số y = 2x + 6 như sau:

Bài 6 trang 79 Toán 8 Tập 1: Tìm hàm số bậc nhất y = ax + b (a ≠ 0) trong mỗi trường hợp sau:

a) Đồ thị của hàm số đó đi qua điểm M(1; 3) và có hệ số góc bằng – 2;

b) Đồ thị của hàm số đó đi qua điểm N(– 1; 4) và song song với đường thẳng y = –3x – 1.

Lời giải:

a) Hàm số bậc nhất y = ax + b có hệ số góc bằng – 2 nên có dạng y = – 2x + b.

Đồ thị của hàm số y = – 2x + b đi qua điểm M(1; 3) thì ta có:

– 2 . 1 + b = 3 suy ra b = 5.

Vậy hàm số bậc nhất cần tìm là y = – 2x + 5.

b) Đồ thị của hàm số y = ax + b song song với đường thẳng y = –3x – 1 nên có dạng y = –3x + b.

Đồ thị của hàm số y = –3x + b đi qua điểm N(– 1; 4) thì ta có:

(–3) . (– 1) + b = 4

3 + b = 4

Suy ra b = 1.

Vậy hàm số bậc nhất cần tìm là y = – 3x + 1.

Bài 7 trang 79 Toán 8 Tập 1: Để sử dụng dịch vụ truyền hình cáp, người dùng phải trả một khoản phí ban đầu và phí thuê bao hằng tháng. Một phần đường thẳng d ở Hình 26 biểu thị tổng chi phí (đơn vị: triệu đồng) để sử dụng dịch vụ truyền hình cáp theo thời gian sử dụng của một gia đình (đơn vị: tháng).

a) Tìm hàm số bậc nhất sao cho đồ thị của hàm số là đường thẳng d.

b) Giao điểm của đường thẳng d với trục tung trong tình huống này có ý nghĩa gì?

c) Tính tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng.

Lời giải:

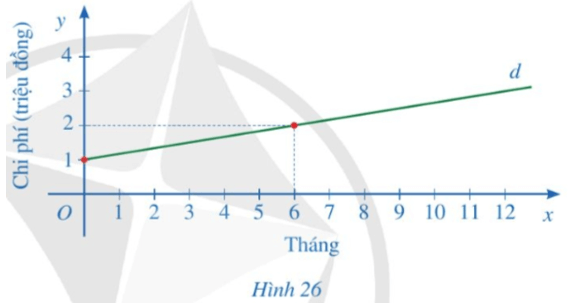
a) Gọi đường thẳng d có dạng y = ax + b.

Trong đó: y là chi phí sử dụng dịch vụ truyền hình cáp (triệu đồng) trong x (tháng).

• Với x = 0 thì y = 1 nên ta có 0x + b = 1 hay b = 1.

Khi đó, hàm số bậc nhất có dạng y = ax + 1.

• Với x = 6 thì y = 2 nên ta có 6a + 1 = 2 hay 6a = 1 suy ra $a=\frac{1}{6}$.

Vậy hàm số bậc nhất biểu diễn đường thẳng d là $y=\frac{1}{6}x+1$.

b) Giao điểm của đường thẳng d với trục tung trong tình huống này là chi phí ban đầu để sử dụng dịch vụ truyền hình cáp là 1 triệu đồng.

c) Tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng là:

$\frac{1}{6}.12+1=2+1=3$ (triệu đồng).

Vậy tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng là 3 triệu đồng.

Bài 8 trang 79 Toán 8 Tập 1: Một kho chứa 60 tấn xi măng, mỗi ngày đều xuất đi m (tấn) với 0 < m < 60. Gọi y (tấn) là khối lượng xi măng còn lại trong kho sau x ngày xuất hàng.

a) Chứng tỏ rằng y là hàm số bậc nhất của biến x, tức là y = ax + b (a ≠ 0).

b) Trong Hình 27, tia At là một phần đường thẳng y = ax + b. Tìm a, b. Từ đó hãy cho biết trong kho còn lại bao nhiêu tấn xi măng sau 15 ngày.

Lời giải:

a) Theo đề bài, mỗi ngày đều xuất đi m (tấn) với 0 < m < 60.

Khi đó, khối lượng xi măng sau x ngày xuất hàng là: mx (tấn).

Khối lượng xi măng còn lại trong kho sau x ngày xuất hàng là: 60 – mx (tấn)

Mà y (tấn) cũng là khối lượng xi măng còn lại trong kho sau x ngày xuất hàng.

Do đó, y = 60 – mx hay y = – mx + 60.

Vậy y là hàm số bậc nhất của biến x.

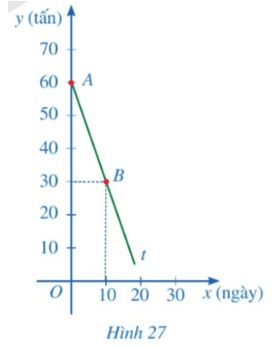
b) Trong Hình 27, ta thấy:

• Điểm A(0; 60):

Với x = 0 thì y = 60 nên ta có: 0x + b = 60 hay b = 60.

Khi đó, đường thẳng cần tìm có dạng y = ax + 60.

• Điểm B(10; 30):

Với x = 10 thì y = 30 nên ta có: 10a + 60 = 30 hay 10a = – 30 suy ra a = – 3.

Khi đó, đường thẳng cần tìm có dạng y = – 3x + 60.

Do đó, số tấn xi măng trong kho còn lại sau 15 ngày là: – 3 . 15 + 60 = 15 (tấn).

Vậy a = – 3; b = 60 và trong kho còn lại 15 tấn xi măng sau 15 ngày.

Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:

Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0)

Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)

Bài 1: Hình chóp tam giác đều

Bài 2: Hình chóp tứ giác đều

Bài tập cuối chương 4