Với giả thiết như ở Ví dụ 3, Cho hình chóp S.ABCD có đáy là hình chữ nhật và SA ⊥ (ABCD)

Luyện tập 3 trang 47 Toán 11 Tập 2: Với giả thiết như ở Ví dụ 3, Cho hình chóp S.ABCD có đáy là hình chữ nhật và SA ⊥ (ABCD). Gọi B', C', D' tương ứng là hình chiếu của A trên SB, SC, SD. Chứng minh rằng:

a) Các mặt phẳng (AB'C'D') và (ABCD) cùng vuông góc với (SAC);

b) Giao tuyến của hai mặt phẳng (AB'C'D') và (ABCD) là đường thẳng đi qua A, nằm trong mặt phẳng (ABCD) và vuông góc với AC.

Trả lời

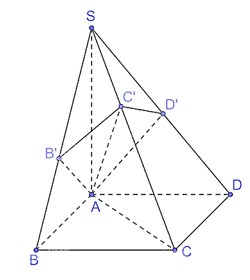
a) Vì B', C', D' tương ứng là hình chiếu của A trên SB, SC, SD nên AB' ⊥ SB, AC' ⊥ SC, AD' ⊥ SD.

Vì SA ⊥ (ABCD) nên SA ⊥ BC, SA ⊥ CD.

Do ABCD là hình chữ nhật nên BC ⊥ AB, CD ⊥ AD.

Vì SA ⊥ BC và BC ⊥ AB nên BC ⊥ (SAB), suy ra (SBC) ⊥ (SAB).

Vì $\left.\begin{array}{l}\left(SBC\right)\cap \left(SAB\right)=SB\\ \left(SBC\right)\perp \left(SAB\right)\\ A{B}^{\text{'}}\subset \left(SAB\right)\\ A{B}^{\text{'}}\perp SB\end{array}\right\}\Rightarrow A{B}^{\text{'}}\perp \left(SBC\right)$$\Rightarrow$AB'⊥SC.

Vì SA ⊥ CD và CD ⊥ AD nên CD ⊥ (SAD), suy ra (SCD) ⊥ (SAD).

Vì $\left.\begin{array}{l}\left(SCD\right)\perp \left(SAD\right)\\ \left(SCD\right)\cap \left(SAD\right)=SD\\ A{D}^{\text{'}}\subset \left(SAD\right)\\ A{D}^{\text{'}}\perp SD\end{array}\right\}\Rightarrow A{D}^{\text{'}}\perp \left(SCD\right)$$\Rightarrow$AD'⊥SC.

Vì $A{B}^{\text{'}}\perp SC$ và $A{D}^{\text{'}}\perp SC$ nên SC ⊥ (AB'C'D') mà SC ⊂ (SAC) nên (SAC) ⊥ (AB'C'D').

Vì SA ⊥ (ABCD) mà SA ⊂ (SAC) nên (SAC) ⊥ (ABCD).

b) Vì $\left.\begin{array}{l}\left(A{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}\right)\cap \left(ABCD\right)=\Delta \\ \left(SAC\right)\perp \left(A{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}\right)\\ \left(SAC\right)\perp \left(ABCD\right)\end{array}\right\}\Rightarrow \Delta \perp \left(SAC\right)$⇒ ∆ ⊥ AC.

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 23: Đường thẳng vuông góc với mặt phẳng

Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng

Bài 25: Hai mặt phẳng vuông góc

Bài 26: Khoảng cách

Bài 27: Thể tích

Bài tập cuối chương 7