Cho hình chóp S.A1.A2...An . Gọi O là hình chiếu của S trên mặt phẳng  

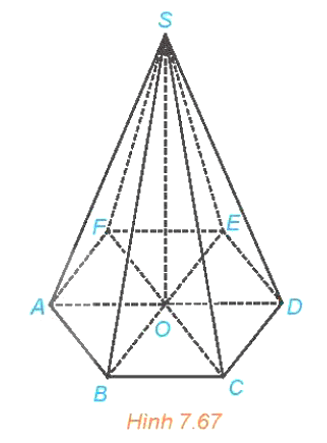
HĐ12 trang 51 Toán 11 Tập 2: Cho hình chóp $S.A_1{A}_2\dots A_n$. Gọi O là hình chiếu của S trên mặt phẳng $\left(A_1{A}_2\dots A_n\right)$ (H.7.67).

a) Trong trường hợp hình chóp đã cho là đều, vị trí của điểm O có gì đặc biệt đối với đa giác đều $A_1{A}_2\dots A_n$?

b) Nếu đa giác $A_1{A}_2\dots A_n$ là đều và O là tâm của đa giác đó thì hình chóp đã cho có gì đặc biệt?

Trả lời

a) Do $S.A_1{A}_2\dots A_n$ là hình chóp đều nên SA₁ = SA₂ = … = SA_n

Vì O là hình chiếu của S trên mặt phẳng $\left(A_1{A}_2\dots A_n\right)$ nên SO ⊥ $\left(A_1{A}_2\dots A_n\right)$.

Xét tam giác SOA₁ vuông tại O, có $O{A}_1=\sqrt{S{A}_1^2-S{O}^2}$,

Xét tam giác SOA₂ vuông tại O, có $O{A}_2=\sqrt{S{A}_2^2-S{O}^2}$,

…..

Xét tam giác SOA_n vuông tại O, có $O{A}_n=\sqrt{S{A}_n^2-S{O}^2}$.

Mà SA₁ = SA₂ = … = SA_n nên OA₁ = OA₂ = … = OA_n hay O là tâm đa giác đều $A_1{A}_2\dots A_n$.

b) Nếu đa giác $A_1{A}_2\dots A_n$ là đều và O là tâm của đa giác đó thì OA₁ = OA₂ = … = OA_n .

Vì O là hình chiếu của S trên mặt phẳng $\left(A_1{A}_2\dots A_n\right)$ nên SO ⊥ $\left(A_1{A}_2\dots A_n\right)$.

Xét tam giác SOA₁ vuông tại O, có $S{A}_1=\sqrt{O{A}_1^2+S{O}^2}$,

Xét tam giác SOA₂ vuông tại O, có $S{A}_2=\sqrt{O{A}_2^2+S{O}^2}$,

…..

Xét tam giác SOA_n vuông tại O, có $S{A}_n=\sqrt{O{A}_n^2+S{O}^2}$.

Mà OA₁ = OA₂ = … = OA_n nên SA₁ = SA₂ = … = SA_n .

Vậy hình chóp $S.A_1{A}_2\dots A_n$ là hình chóp đều.

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 23: Đường thẳng vuông góc với mặt phẳng

Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng

Bài 25: Hai mặt phẳng vuông góc

Bài 26: Khoảng cách

Bài 27: Thể tích

Bài tập cuối chương 7