Vẽ parabol y = 3x^2 – 10x + 7. Từ đó tìm khoảng đồng biến, nghịch biến

Vẽ parabol y = 3x² – 10x + 7. Từ đó tìm khoảng đồng biến, nghịch biến và giá trị nhỏ nhất của hàm số y = 3x² – 10x + 7.

Trả lời

Hệ số a của hàm số y = 3x² – 10x + 7 là a = 3 > 0 nên parabol quay bề lõm hướng lên trên.

Parabol y = 3x² – 10x + 7 có:

- Tọa độ đỉnh I$\left(\frac{5}{3};-\frac{4}{3}\right)$;

- Trục đối xứng $x=\frac{5}{3}$;

- Giao điểm của đồ thị với trục Oy là A(0; 7).

- Parabol cắt trục hoành tại hai điểm có hoành độ là nghiệm của phương trình 3x² – 10x + 7 = 0, tức là x = $\frac{7}{3}$ và x = 1 hay parabol cắt trục hoành tại các điểm D(1; 0) và $E\left(\frac{7}{3};0\right)$;

- Điểm đối xứng với điểm A qua trục đối xứng $x=\frac{5}{3}$ là B$\left(\frac{10}{3};7\right)$.

Vẽ đường cong đi qua các điểm trên ta được parabol y = 3x² – 10x + 7.

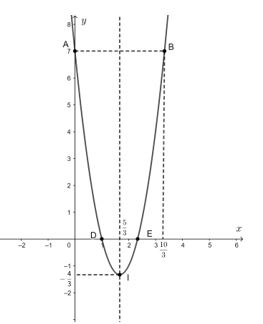
- Đồ thị hàm số đi xuống từ trái qua phải trên khoảng $\left(-\infty ;\frac{5}{3}\right)$ nên hàm số nghịch biến trên khoảng $\left(-\infty ;\frac{5}{3}\right)$.

- Đồ thị hàm số đi lên từ trái qua phải trên khoảng $\left(\frac{5}{3};+\infty \right)$ nên hàm số đồng biến trên khoảng $\left(\frac{5}{3};+\infty \right)$.

- Điểm thấp nhất của đồ thị là đỉnh I$\left(\frac{5}{3};-\frac{4}{3}\right)$ nên giá trị nhỏ nhất của hàm số là $y=-\frac{4}{3}$ tại $x=\frac{5}{3}$.